IEEE 754

　ほぼすべてのコンピュータ・プログラムの浮動小数点算術は、IEEE754の仕様に準拠しています。インテルによって考案された浮動小数点の考え方が１９８５年に標準として制定され、２００８年に改定されています。正式名称は、IEEE Standard for Floating-Point Arithmetic (ANSI/IEEE Std 754-2008)です。

　この中で規定されている基本形式のうち、エクセルが実装しているのは64ビット二進浮動小数点形式（倍精度・double）で、以下のように符号部(sign)、指数部(exponent)、仮数部(fraction)の3つの情報に分かれます。

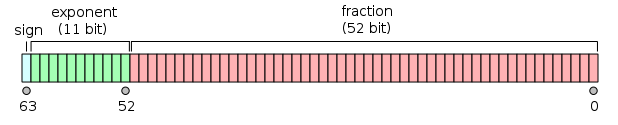
　すべてのコンピューターは、数値が格納されるメモリのビット数が定められており、格納できる最大または最小は有限です。

浮動小数点演算

　ありきたりの数値と思われる 0.1 という値は、2進数では無限循環小数となってしまいます。値が無限に循環していますから、いつまでも終りがありません。

符号 = 0
指数 = 01111111011
仮数 = 1001100110011001100110011001100110011001100110011010.....

　つまり、浮動小数点演算で0.1を3回足した場合に0.3にならないという現象がみれます。
　エクセルのスプレッドシートでB1からB3までの0.1をB4でSUM関数を使って合計してやると、以下のように0.3になっています。このB4セルの値を0.3と比較しても、TRUEを表示します。

　しかし、エクセルブックを一旦保存し、エクセルの中に格納されている状態を見ると、以下のようになっています。

<sheetData>
    <row r="1" spans="1:2" x14ac:dyDescent="0.4">
        <c r="B1">
            <v>0.1</v>
        </c>
    </row>
    <row r="2" spans="1:2" x14ac:dyDescent="0.4">
        <c r="B2">
            <v>0.1</v>
        </c>
    </row>
    <row r="3" spans="1:2" x14ac:dyDescent="0.4">
        <c r="A3" s="1"/>
        <c r="B3" s="1">
            <v>0.1</v>
        </c>
    </row>
    <row r="4" spans="1:2" x14ac:dyDescent="0.4">
        <c r="A4" t="s">
            <v>0</v>
        </c>
        <c r="B4" s="2">
            <f>SUM(B1:B3)</f>
            <v>0.30000000000000004</v>
        </c>
    </row>
</sheetData>

　「r="B4"」の値「v」は、0.30000000000000004 となっています。

　このエクセルをデータソースとしてPower Bで読み込んだ場合は、Power Query上では以下のように、0.30000000000000004　となります。

　0.3と比較してやると、以下のように False になります。

　これを回避するには、値を固定小数点にして読み込めば、Trueになります。

一旦の結論

　浮動小数点データは、データモデルが大きくなる原因となり、計算が合わないことがあります。エクセルの数値データをエクセルに持ってくるには、

ファクトテーブルに浮動小数点の数値をできるだけ持ち込まない。
小数点以下の数値が必要な場合は、小数点以下４桁を保持する固定小数点、通貨型で読み込む

　この２つを心がけてみてはいかがでしょうか。

[Power BI] Power Queryの『型』を探る (3) number 蛇足

IEEE 754

浮動小数点演算

一旦の結論

関連記事