RNNを用いて周期データ予測をしたかった

参考: わかりやすいPyTorch入門⑥（RNN：再帰型ニューラルネットワーク） - エクスチュア株式会社ブログ

RNNを用いて周期データ予測をし、RNNのすごさを体験しようとして肩透かしを食った事例を紹介します。

経緯

参考にある記事をもとにRNNによる周期データ予測はできたのですが、単純なNNと対比したほうが分かりやすいと思い、ネットをRNNを使わないものに変更したところ、精度があまり変わりませんでした。

大まかな流れ

まず、単純なNNでx軸からy軸を予測します。そして、単純なNNで過去のy軸データから現在のy軸データを予測し、最後にRNNで過去のy軸データから現在のy軸データを予測します。

環境の準備

インポートとか、使うデータの用意とかします。

コード解説

import torch
import torch.nn as nn
from torch import optim
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torch.utils.data import TensorDataset
import numpy as np
import matplotlib.pyplot as plt

GPUを使えたら使います。

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print(device)

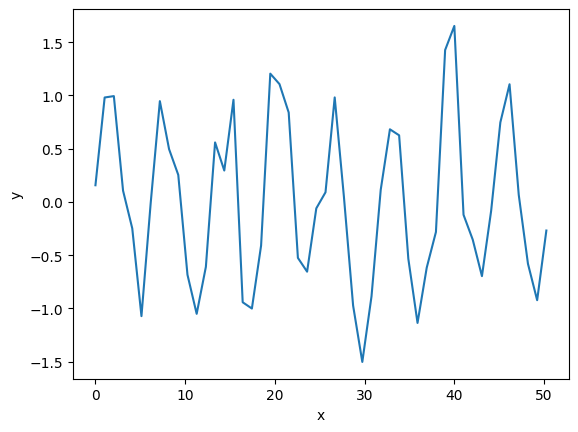
正弦波にノイズを加えて周期データを生成します。

# --- 1. データ生成 ---
data_x= np.linspace(0, 16*np.pi)
data_y = np.sin(data_x) + np.random.normal(0, 0.3, len(data_x)) #ノイズを加える

plt.plot(data_x, data_y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

こんなデータができます。

ハイパーパラメータはこんな感じにしました。

# ハイパーパラメータ
# 過去10件のデータを訓練データにする(ウィンドウサイズ)
window_size = 10
batch_size = 8

単純な手法による周期データ予測

まずは、訓練データをx軸、正解ラベルをy軸という風にして学習させます。
もちろん未知のxの値に対応できないので失敗します。

コード解説

とりあえず、データの前半8割を訓練データ、後半2割をテストデータにします。

# データを訓練データとテストデータに分割する
# 今回は前半8割を訓練データ、後半2割をテストデータにする
data_size = len(data_x)
train_size = int(data_size * 0.8)
test_size = data_size - train_size
x_train = data_x[:train_size]
y_train = data_y[:train_size]
x_test = data_x[train_size:]
y_test = data_y[train_size:]

訓練データを作成します。

# 訓練用のデータとラベルを作成

x_train = torch.FloatTensor(x_train)
y_train = torch.FloatTensor(y_train)

trainset = TensorDataset(x_train, y_train)
trainloader = DataLoader(trainset, batch_size=batch_size, shuffle=True)

#確認用
x, t = next(iter(trainloader))
print("x: ", x[:3])
print("t: ", t[:3])

テストデータも同様です。

# テスト用のデータとラベルを作成

x_test = torch.FloatTensor(x_test)
y_test = torch.FloatTensor(y_test)

testset = TensorDataset(x_test, y_test)
testloader = DataLoader(testset, batch_size=batch_size, shuffle=False)

#確認用
x, t = next(iter(trainloader))
print("x: ", x[:3])
print("t: ", t[:3])

予測器はこんな感じです。

class Predictor(nn.Module):
    def __init__(self):
        super(Predictor, self).__init__()
        self.fc1 = nn.Linear(1, 64)
        self.fc2 = nn.Linear(64, 1)
        self.relu = nn.ReLU()
    def forward(self, x):
        # x の形状は (batch_size)
        x = x.unsqueeze(1) # (batch_size, 1)に変換する
        x = self.fc1(x)
        x = self.relu(x)
        y = self.fc2(x)
        return y
predictor = Predictor().to(device)
predictor

評価関数は平均二乗誤差、最適化手法はAdamです。

criterion = nn.MSELoss()
optimizer = optim.Adam(predictor.parameters(), lr=0.001)

訓練します。

# 学習
def train(net, epoch_n):
  net.train()

  for epoch in range(epoch_n):
      epoch_loss = 0.0
      for x, t in trainloader:

          x, t = x.to(device), t.to(device)
          optimizer.zero_grad()
          y = net(x)
          loss = criterion(y, t)
          loss.backward()
          optimizer.step()
          epoch_loss += loss.item()

      if epoch % (epoch_n/10) == 0:
        print(f'Epoch [{epoch}/{epoch_n}] Loss: {epoch_loss / len(trainloader)}')

# 学習実行
train(predictor, 1000)

未知のデータ(テストデータ)で予測します。

predictor.eval()
with torch.no_grad():
  predicted = []
  accuracy = 0
  for x, t in testloader:
    y = predictor(x)
    accuracy += criterion(y, t)
    predicted.extend(y.flatten())

print("精度: ", accuracy / len(testloader))
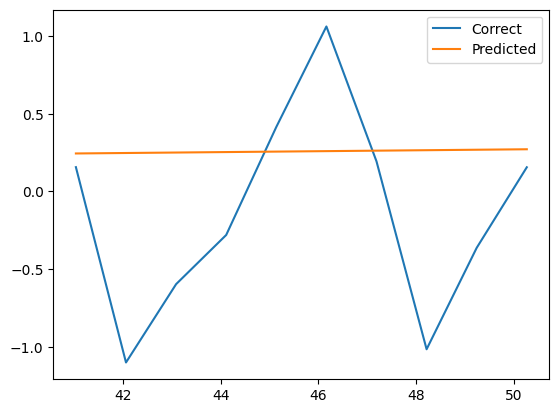
plt.plot(data_x[-test_size:], data_y[-test_size:], label="Correct")
plt.plot(data_x[-test_size:], predicted, label="Predicted")
plt.legend()
plt.show()

すると、以下のように、残念な予測をします。
これは、未知のxの値が来て、とりあえず無難な値である平均値を返している状況です。

時系列を考慮してデータを再編成する

前章の失敗は、データを時系列データとして扱っていないことに起因します。
そのため、今回は訓練データを過去のy軸データ、正解ラベルを現在のy軸データとします。

# データを訓練データとテストデータに分割する
# 今回は前半8割を訓練データ、後半2割をテストデータにする
data_size = len(data_x)
raw_train_size = int(data_size * 0.8)
raw_test_size = data_size - raw_train_size
x_train = data_x[:raw_train_size]
y_train = data_y[:raw_train_size]
x_test = data_x[raw_train_size-window_size:] # 予測用のデータ(最初の10件)を取っておく
y_test = data_y[raw_train_size-window_size:]

# 最初の方のデータは過去のデータが無いので論理的に除外する
train_size = raw_train_size - window_size
test_size = raw_test_size

過去のデータを訓練データとする以上、最初の方のデータは使えません。
そのため、実際に使うデータは、用意されたデータより少し少なくなります。
(ですが、テストデータに関しては、訓練データと少し重ねることで、上記のロスを回避しています。)

訓練データを用意します。

# 訓練用のデータとラベルを作成
train_data = np.zeros((train_size, window_size, 1))
labels = np.zeros((train_size, 1))
for i in range(train_size):
    # i+window_size-1までが訓練データ
    # i+window_sizeが正解ラベル
    train_data[i] = y_train[i:i+window_size].reshape(-1, 1)
    labels[i] = [y_train[i+window_size]]

train_data = torch.FloatTensor(train_data)
labels = torch.FloatTensor(labels)

trainset = TensorDataset(train_data, labels)
trainloader = DataLoader(trainset, batch_size=batch_size, shuffle=True)

#確認用
y, t = next(iter(trainloader))
print("y: ", y[:3])
print("t: ", t[:3])

同様にテストデータを用意します。

# テスト用のデータとラベルを作成
test_data = np.zeros((test_size, window_size, 1))
labels = np.zeros((test_size, 1))
for i in range(test_size):
    # i+window_size-1までが訓練データ
    # i+window_sizeが正解ラベル
    test_data[i] = y_test[i:i+window_size].reshape(-1, 1)
    labels[i] = [y_test[i+window_size]]

test_data = torch.FloatTensor(test_data)
labels = torch.FloatTensor(labels)

testset = TensorDataset(test_data, labels)
testloader = DataLoader(testset, batch_size=batch_size, shuffle=False)

#確認用
y, t = next(iter(testloader))
print("y: ", y[:3])
print("t: ", t[:3])

過去データで訓練されたモデルによる周期データ予測

ここが問題の部分です。
とりあえず以下のネットを見てください。

class TimeLinePredictor(nn.Module):
    def __init__(self):
        super(TimeLinePredictor, self).__init__()
        self.fc1 = nn.Linear(window_size, 64)
        self.fc2 = nn.Linear(64, 1)
        self.relu = nn.ReLU()
    def forward(self, x):
        # x の形状は (batch_size, window_size, 1)
        x_batch_size = x.size(0) # 最後のあまりのバッチサイズは少し小さい
        x = x.view(x_batch_size, window_size)
        x = self.fc1(x)
        x = self.relu(x)
        y = self.fc2(x)
        return y
tlPredictor = TimeLinePredictor().to(device)
tlPredictor

これは、先の時系列データに対応するように細工しただけの普通のNNです。
これで予測してみます。
(評価関数とか、訓練とかは、今までのコードと同じです)

tlPredictor.eval()
with torch.no_grad():
  predicted = []
  accuracy = 0
  for x, t in testloader:
    y = tlPredictor(x)
    accuracy += criterion(y, t)
    predicted.extend(y.flatten())

print("精度: ", accuracy / len(testloader))
plt.plot(data_x[-test_size:], data_y[-test_size:], label="Correct")
plt.plot(data_x[-test_size:], predicted, label="Predicted")
plt.legend()
plt.show()

すると、こんな結果になりました。
(colabのセッションを再起動したせいでデータのノイズが変化していますが、見なかったふりをして下さい)

よく予測できていますね。
(予測はできて正弦波の成分までで、ランダムなノイズは予測不可ですから、結構いい感じに予測はできてます)
では、RNNだと、さぞ正確に予測してくれるのだろうと思い、ネットを以下に変えてみました。

class RNNPredictor(nn.Module):
    def __init__(self):
        super(RNNPredictor, self).__init__()
        self.rnn = nn.RNN(input_size=1, hidden_size=64, batch_first=True)
        self.fc = nn.Linear(64, 1)

    def forward(self, x):
        # x の形状は (batch_size, window_size, 1)
        x = x.to(device)
        x_rnn, hidden = self.rnn(x, None)
        # x_rnn は (batch_size, window_size, hidden_size) の形状になる
        x = self.fc(x_rnn[:, -1, :])
        return x
rnnPredictor = RNNPredictor().to(device)

すると、以下の結果になりました。

変わってない！！
むしろ、平均二乗誤差を算出すると、下がっていました。
そこで、geminiくんに質問してみた結果、以下のようなことを言われました。

• 過去のデータから1件の未来のデータを予測するくらいは普通のNNでできる
• RNN系列のモデルが役立つのは、長期的な未来の予測
• RNNは理論上のもので、実際に有用なのはLSTMやGRUといったゲート付きRNN

つまり、今回やろうとしていたくらいではRNNの良さは分からず、RNNの良さが分かるようなタスクはもっと複雑なものということです。
さらに、そのタスクをこなすためにはゲート付きのものを使う必要が出てくるということです。
ということで、そのうちLSTMかGRUを用いてRNN系列のモデルのすごさを体験したいと思います。

追記: Geminiくんに怒られたので補足します。

単純な正弦波予測でも、RNN（あるいはLSTM）が全結合層より圧倒的に有利なケースは存在します（例：可変長の過去データを使う場合や、位相が複雑に変化する場合など）。