Python機械学習プログラミング備忘録 3.3

はじめに

オンライン機械学習講義の復習用。(2021/05/05現在)

Python機械学習プログラミング
達人データサイエンティストによる理論と実践
の以下を取り扱います。

• 第3章 分類問題 (3.3)

ここでは、数式による理論の理解と
sklearn を使った実装による理解を目指します。

対象データ: Iris データセット

目次

1. 開発環境
2. パーセプトロンの問題点
3. 事象の起こりやすさを表すオッズ比
4. ロジット関数の定義
5. ロジット関数の逆関数がロジスティック関数
6. シグモイド関数の実装
7. クラスの所属関係の確率を見積もる
8. 重みの更新
9. Irisデータをロード
10. ロジスティック回帰の学習
11. 学習結果の可視化
12. まとめ
13. 参考文献

開発環境

MacBook Air 2017
macOS Catalina 10.15.16

Google Colaboratory
sklearn: 0.22.2.post1

numpy: 1.19.5
matplotlib: 3.2.2

パーセプトロンの問題点

前回、パーセプトロンを実装し、
その学習アルゴリズムが
実社会で使われない理由が見えました。

最大の問題点は、
完全に線形分離できないクラスがあると
収束しない点です。

エポックごとに誤分類されるサンプルが
一つでもあった場合、重みが絶えず更新されてしまうのです。

この点を踏まえ、線形分類問題に対して、
より柔軟性を持つロジスティック回帰を見ていきます。
※ その名前とは裏腹に、回帰ではなく分類のためのモデルになります。

ロジスティック回帰は、
産業界で広く利用されている分類アルゴリズムの一つで、
線形分類可能なクラスに対して、高い性能を発揮します。
※ 二値分類のための線形モデルですが、多値分類モデルとして拡張できます。

事象の起こりやすさを表すオッズ比

ロジスティック回帰の概念には、
オッズ比（odds ratio）の理解が欠かせません。

odds\,ratio :  \frac{p}{1-p}

オッズ比は事象の起こりやすさを表したもので、
$p$ には正事象の確率が入ります。
※ 正事象は予測したい事象のことで、通常 $y = 1$ として考えます。

ロジット関数の定義

オッズ比の対数をとったものは対数オッズと呼ばれ、
これを関数とみなしたものがロジット関数になります。

logit(p) = \log \frac{p}{1-p} \,(0 < p < 1)\\
\\

ロジット関数は、
0より大きく、1より小さい範囲の入力値を受け取り、
実数の全範囲に変換します。

ここで、注目すべきは入力値です。

上式では確率 $p$ が「分かったもの」として扱っていましたが、
実際には、その確率 $p$ を求めなければなりません。

なぜなら最終的にやりたいことは、二値分類であり、
そのクラスに属する確率 $p$ を出力したいからです。

この関数は後ほど使います。

ロジット関数の逆関数がロジスティック関数

ここで、
一般的な線形分離の決定境界 $z$ は以下の式で表現できますが、

z = w_0x_0 + w_1x_1 + \,... + \,w_mx_m = \sum_{i=0}^{m}w_ix_i = \boldsymbol{w^Tx}\\
\\

これでは、$z$ の取りうる値が $-\infty$ から $\infty$ になります。

しかし、予測したい $p$ は確率なので、
出力値は、0 から 1 の間に収まっていなければなりません。

上式では $p \neq z$ となるため、
$z$ の取りうる範囲が 0 から 1 の値に収まるように、
リンク関数として、ロジット関数を導入します。

logit(p\,(y = 1 \,| \,\boldsymbol{x}) = z
\\

※ $logit(p\,(y = 1 \,| \,\boldsymbol{x})$ は、特徴量 $\boldsymbol{x}$ が与えられたときに、
サンプルクラスが1に属する条件付き確率を表しています。

※ 確率 $p$ の変換に使う関数をリンク関数と呼んでいます。

今回はリンク関数が対数であるため、
右辺を指数と見立て、その逆関数を導き出します。

\\
\log \frac{p}{1-p} = z\\

まずは対数の性質から式変形です。

e^{z} = \frac{p}{1-p}\\
e^{z} - e^{z}p = p\\

あとは単純な式変形です。

\begin{align}
p &= \frac{e^{z}}{e^{z}+1}\\
&= \frac{1}{1+e^{-z}}\\
\\
\end{align}

上式はロジット関数の逆関数から得られた結果です。

$z$ は総入力となっており、
取りうる値の「$-\infty$ から $\infty$」を「0 から 1」に変換します。
これで、
サンプルクラスが1に属する確率 $p$ を計算できるようになりました。

このようにして導かれた関数は、ロジスティック関数と呼ばれ、
改めて関数として記載しますと、以下の通りになります。

\phi(z)= \frac{1}{1+e^{-z}} 

$z$ は総入力を表しています。

z = \boldsymbol{w^Tx} = w_0x_0 + w_1x_1 + \,... + \,w_mx_m\\
\\

ところで、このロジスティック関数は
他の分野では標準シグモイド関数と呼ばれ、
機械学習の人たちだけが、ロジスティック関数と呼ぶらしいです。

シグモイド関数は、上記の式において、
本来ならば $z$ の前に $a$ （ゲイン）を伴いますが、
標準シグモイド関数は、そのゲインが $a=1$ になるため、
「標準」と呼ぶのだそうです。

※ ここでは今後も、この標準シグモイド関数を
ロジスティック関数、もしくはシグモイド関数と呼び続けることにします。

シグモイド関数の実装

collaboratory 上でシグモイド関数を実装します。

ipynb

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(z):
  return 1.0 / (1.0 + np.exp(-z))

# 0.1間隔で-7以上7未満のデータを生成
z = np.arange(-7, 7, 0.1)
# 生成したデータでシグモイド関数を実行
phi_z = sigmoid(z)
# 元のデータとシグモイド関数の出力をプロット
plt.plot(z, phi_z)
# 垂直線を追加
plt.axvline(0.0, color='k')
# y軸の上限/下限を設定
plt.ylim(-0.1, 1.1)
# 軸のラベルを設定
plt.xlabel('$\phi (z)$')
# y軸の目盛りを追加
plt.yticks([0.0, 0.5, 1.0])
# Axesクラスのオブジェクトの取得
ax = plt.gca()
# y軸のメモリに合わせて水平グリッド線を追加
ax.yaxis.grid(True)
# グラフを表示
plt.show()

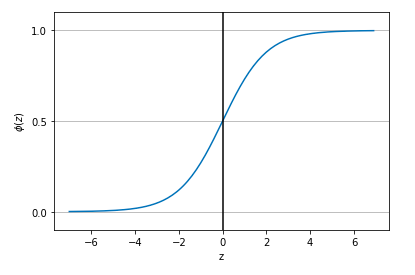
これを実行すると、以下の図のようなシグモイド曲線が得られます。

ポイントは以下の通りです。

• $z$ が無限大に向かう場合（$z \to \infty$）は $\phi(z)$ が 1 に近づく
• $z$ が負の無限大に向かう場合（$z \to -\infty$）は $\phi(z)$ が 0 に近づく

そのため、シグモイド関数は実数値を入力として受け取り、
$\phi(z)= 0.5$ を切片として、それらを $[0, 1]$ の範囲の値に出力します。

またグラフの特徴的な形（S字）からシグモイドと呼ぶのだそうです。

クラスの所属関係の確率を見積もる

次はシグモイド関数の出力を見ていきます。

サンプルが 1 に属している確率は以下の式で解釈できます。

\phi(z) = P(y=1\,| \,\boldsymbol{x};\boldsymbol{w})\\
\\

上式はロジスティック回帰の重み $\boldsymbol{w}$ が所与のとき、
特徴量 $\boldsymbol{x}$ が与えられた条件のもとで $y=1$ になる条件付き確率を表しています。

例えば、Iris データセットの２つの品種の
Iris-Versicolor ( $y=1$ ) と Iris-Setosa ( $y=0$ ) を分類するとき、
$\phi(z)= P(y=1\,| \,\boldsymbol{x};\boldsymbol{w})=0.8$ が算出される場合、
このサンプルが Iris-Versicolor である確率が 80% であることを意味します。

同様にこのサンプルが Iris-Setosa である確率は、
$P(y=0\,| \,\boldsymbol{x};\boldsymbol{w})= 1 - P(y=1\,| \,\boldsymbol{x};\boldsymbol{w}) = 0.2$ （20%）として計算できます。

クラスに属する確率を求めた後は、
量子化器（単位ステップ関数）を使って予測された確率を二値の値に変換するだけです。

\hat{y} = \left\{
\begin{array}{ll}
1 & \phi(z) \geq 0.5 \\
0 & \phi(z) \lt 0.5
\end{array}
\right.\\
\\

また総入力に着目した場合、これは以下と等価になります。

\hat{y} = \left\{
\begin{array}{ll}
1 & z \geq 0.0 \\
0 & z \lt 0.0
\end{array}
\right.\\
\\

このように、予測されるクラスラベルは、
所属クラスのみに関心があるだけでなく、
どのくらいの確率で所属しているのかを調べる際に役立ちます。

例えば、以下の例ではロジスティック回帰は力を発揮するでしょう。

• 気象予報における降水確率（雨が降るかどうかの確率に加えて）
• 患者が特定の疾患にかかっている確率（特定の症状である確率に加えて）

重みの更新

次は、ロジスティック回帰のコスト関数を見ていきます。

まずは予測の信頼度として、
以下のように尤度 $L$ （結果から見た条件のもっともらしさ）を定義します。

L(\boldsymbol{w}) = P\,(\boldsymbol{y}\,| \,\boldsymbol{x};\boldsymbol{w}) = \prod_{i=1}^{n}P\,\Bigl(y^{(i)}\,| \,x^{(i)};\boldsymbol{w}\Bigr) = \prod_{i=1}^{n}\Bigl(\phi\Bigl(z^{(i)}\Bigr)\Bigr)^{y^{(i)}}\Bigl(1 - \phi\Bigl(z^{(i)}\Bigr)\Bigr)^{1-y^{(i)}}\\
\\
\\

第３項目は、各サンプルのクラスラベルの条件付き確率を表しており、
それを第４項目では積の形として、計算することを意味します。

このように、一つの式で
クラスラベル（0 or 1）の確率分布を同時に満たせるようになりました。

しかし、より簡単に計算できるよう対数を取り、和の形で表現できるようにします。

l(\boldsymbol{w}) = \log L(\boldsymbol{w}) = \sum_{i=1}^{n}\Bigl[y^{(i)} \log \Bigl(\phi \Bigl(z^{(i)}\Bigr)\Bigr) + \Bigl(1 - y^{(i)}\Bigr) \log \Bigl(1 -\phi\Bigl(z^{(i)}\Bigr)\Bigr)\Bigr]\\
\\
\\

$l(\boldsymbol{w})$ は対数尤度（log-likelihood）関数を表しており、
先ほどの積の形より尤度の最大化を容易にします。

また、一般にモデルの性能を評価する際には、
モデルの「良さ」ではなく、「悪さ」を指標にして、
その最小値を求めるのが普通です。

そのため、対数尤度 $l(\boldsymbol{w})$ をコスト関数 $J(\boldsymbol{w})$ として書き直すと
以下のようになります。

J(\boldsymbol{w}) = - \log L(\boldsymbol{w}) = \sum_{i=1}^{n}\Bigl[- y^{(i)} \log \Bigl(\phi \Bigl(z^{(i)}\Bigr)\Bigr) - \Bigl(1 - y^{(i)}\Bigr) \log \Bigl(1 -\phi\Bigl(z^{(i)}\Bigr)\Bigr)\Bigr]\\
\\
\\

この関数について、
例えばサンプルが一つ（$n=1$）の場合、
上式は以下のようになります。

\begin{align}
J\bigl(\phi(z), y; \boldsymbol{w}\bigr) = -y \log\bigl(\phi(z)\bigr) - \bigl(1 - y\bigr)\log\bigl(1 - \phi(z)\bigr)\\

\end{align}\\
\\

$y=0$ の場合、一項目が 0 になり、
$y=1$ であれば二項目が 0 になります。

J\bigl(\phi(z), y; \boldsymbol{w}\bigr) = \left\{
\begin{array}{ll}
- \log \bigl(\phi(z)\bigr) & (y = 1)\\ 
- \log \bigl(1 - \phi(z)\bigr) & (y = 0)
\end{array}
\right.\\
\\

次に、この関数を可視化します。

cost_function

def cost_1(z):
    return - np.log(sigmoid(z))

def cost_0(z):
    return - np.log(1 - sigmoid(z))

z = np.arange(-10, 10, 0.1)
phi_z = sigmoid(z)

c1 = [cost_1(x) for x in z]
plt.plot(phi_z, c1, label='J(w) if y=1')

c0 = [cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle='--', label='J(w) if y=0')

plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

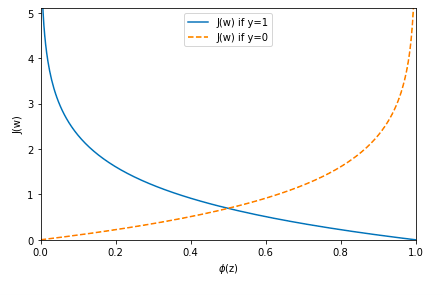
以下のグラフは一つのサンプルに対するコスト関数です。

ここで、コスト関数の勾配を計算するために、
ロジスティック関数 $\phi(z)$ を $z$ で微分しておきます。

\begin{align}
\frac{\partial}{\partial z} \phi(z) &= \frac{\partial}{\partial z} \frac{1}{1+e^{-z}}\\
\\
&= \frac{e^{-z}}{(1+e^{-z})^2} \\
\\
&= \frac{1}{1+e^{-z}}\Big(1 - \frac{1}{1+e^{-z}}\Big) \\
\\
&= \phi(z)\big(1 - \phi(z)\big)\\
\\
\end{align} 

続いて、コスト関数 $L(\boldsymbol{w})$ を $j$ 番目の重み $w_j$ で微分します。
式変形、少し大変です。

\begin{align}
\frac{\partial}{\partial w_j} J(\boldsymbol{w}) &= - \frac{\partial}{\partial w_j}\sum_{i=1}^{n}\Bigl[y^{(i)} \log \Bigl(\phi \Bigl(z^{(i)}\Bigr)\Bigr) + \Bigl(1 - y^{(i)}\Bigr) \log \Bigl(1 -\phi\Bigl(z^{(i)}\Bigr)\Bigr)\Bigr]\\
\\
&= - \sum_{i=1}^{n}\Bigl[y^{(i)} \frac{\partial}{\partial \,\phi\bigl(z^{(i)}\bigr)} \log \Bigl(\phi \Bigl(z^{(i)}\Bigr)\Bigr) + \Bigl(1 - y^{(i)}\Bigr) \frac{\partial}{\partial \,\phi \bigl(z^{(i)}\bigr)} \log \Bigl(1 -\phi\Bigl(z^{(i)}\Bigr)\Bigr)\Bigr]\\
\\
&= - \sum_{i=1}^{n}\Biggl[y^{(i)} \frac{\partial \log \Bigl(\phi \Bigl(z^{(i)}\Bigr)\Bigr)}{\partial \,\phi\bigl(z^{(i)}\bigr)}\frac{\partial \,\phi \bigl(z^{(i)}\bigr)}{\partial \,z^{(i)}} \frac{\partial \,z^{(i)}}{\partial \,w_j} + \Bigl(1 - y^{(i)}\Bigr) \frac{\partial \log \Bigl(1 -\phi\Bigl(z^{(i)}\Bigr)\Bigr)}{\partial\,\phi \bigl(z^{(i)}\bigr)} \Biggr]\\
\\
&= - \sum_{i=1}^{n} \Biggl[y^{(i)} \frac{\phi\bigl(z^{(i)}\bigr)}{\phi\bigl(z^{(i)}\bigr)} \Big(1 - \phi\Bigl(z^{(i)}\Bigr)\Bigr)x_{ij} + \Bigl(1 - y^{(i)}\Bigr) \frac{\partial \log \Bigl(1 -\phi\Bigl(z^{(i)}\Bigr)\Bigr)}{\partial\,\phi \bigl(z^{(i)}\bigr)}\frac{\partial \,\phi \bigl(z^{(i)}\bigr)}{\partial \,z^{(i)}} \frac{\partial \,z^{(i)}}{\partial \,w_j}\Biggr] \\
\\
&= - \sum_{i=1}^{n} \Biggl[y^{(i)} \Big(1 - \phi\Bigl(z^{(i)}\Bigr)\Bigr)x_{ij} - \frac{\Bigl(1 - y^{(i)}\Bigr)}{\Bigl(1 - \phi\bigl(z^{(i)}\bigr)\Bigr)}\phi \Bigl(z^{(i)}\Bigr)\Big(1 - \phi\Bigl(z^{(i)}\Bigr)\Bigr)x_{ij}\Biggr] \\
\\
&= - \sum_{i=1}^{n} \Bigl[y^{(i)} \Big(1 - \phi\Bigl(z^{(i)}\Bigr)\Bigr)x_{ij} - \Bigl(1 - y^{(i)}\Bigr)\phi \Bigl(z^{(i)}\Bigr)x_{ij}\Bigr] \\
\\
&= - \sum_{i=1}^{n} \Bigl(y^{(i)} - \phi \Bigl(z^{(i)}\Bigr)\Bigr)\,x_{ij} \\
\\
\end{align} 

※ 途中式が長くなるのを防ぐために一項づつ計算しているところがあります。

上式がコスト関数の勾配です。
これに学習率 $\eta $ をかけ、重み $w_j$ を更新します。

\Delta w_j = - \eta \Bigl(- \sum_{i=1}^{n} \Bigl(y^{(i)} - \phi \Bigl(z^{(i)}\Bigr)\Bigr)\,x_{ij}\Bigr)\\
\\
\\
w_j \leftarrow w_{j} + \Delta w_j
\\

ここまで、一通りロジスティック回帰を見てきました。
次は実装です。

Irisデータをロード

colab notebook に入力して
sklearn のバージョンを確認します。

ipynb

import sklearn
print(sklearn.__version__) # 0.22.2.post1

2021/05/05 現在、colab notebook ではデフォルトで
上記のバージョンが使用されるようです。

※ バージョンによっては、これより下のコードの整合性が取れないことがあるかもしれません。

続いて、以下のコードで学習に必要なデータをロードし、
X に特徴量、y にラベルを格納します。

ipynb

from sklearn import datasets
import numpy as np

iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 2: petal length, 3: petal width
y = iris.target

前回同様、データをグラフにプロットしたいので、
考慮する特徴量は、
花びらの長さ（petal length）と
花びらの幅（petal width）のみになります。

以下のコードでラベルの確認をします。

ipynb

print("Class labels: ", np.unique(y)) # [0 1 2]

Iris-Setosa: 0, Iris-Versicolor: 1, Iris-Virginica: 2
として、与えられています。

ロジスティック回帰の学習

次にモデルの汎化性能を確保するために、
データ全体から
トレーニングデータセットとテストデータセットに
分割します。

以下のコードで、
テストデータの割合を30%（45個のサンプル）に指定します。

ipynb

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)

続いて特徴量のスケーリングを行います。

各特徴量の取りうる値を揃えるために、
StandardScalerを使います。

以下のコードで、標準化できます。

ipynb

from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
# fitメソッドで平均と標準偏差を計算
sc.fit(X_train)
X_train_std = sc.transform(X_train) # transformメソッドで標準化
X_test_std = sc.transform(X_test)

StandardScalerのfitメソッドを使うと
特徴量ごとの平均 μ と標準偏差 σ を計算できます。

これらのパラメータを使い、
transform メソッドでトレーニングデータを標準化します。

テストデータにも
同じスケーリングパラメータを適用したのは、
相互の基準を揃え、比較できるようにするためです。

これでロジスティック回帰をトレーニングできる状態になりました。

以下のコードで、
ロジスティック回帰のインスタンスを作成し、
トレーニングを実行します。

ipynb

from sklearn.linear_model import LogisticRegression

# インスタンスの生成
lr = LogisticRegression(random_state=0)
# トレーニングデータをモデルに適合させる
lr.fit(X_train_std, y_train)

※ 正則化パラメータはデフォルト（C=1.0）の値が適用されます。

学習結果の可視化

続いて、
トレーニングしたモデルを可視化します。

モデルの決定領域をプロットし、
未知のデータに対してその程度識別できるか見ていきます。

以下のコードで、描画の定義をします。

ipynb

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt

def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
  # マーカーとカラーマップの準備
  markers = ('s', 'x', '^', 'v')
  colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
  cmap = ListedColormap(colors[:len(np.unique(y))])

  # 決定領域のプロット
  x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
  x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1

  # グリッドポイントの生成
  xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                                      np.arange(x2_min, x2_max, resolution))

  # 各特徴量を1次元配列に変換して予測を実行
  Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
  # 予測結果を元にグリッドポイントのデータサイズに変換
  Z = Z.reshape(xx1.shape)
  # グリッドポイントの等高線をプロット
  plt.contourf(xx1, xx2, Z, alpha=0.5, cmap=cmap)
  # 軸の範囲を設定
  plt.xlim(xx1.min(), xx1.max())
  plt.ylim(xx2.min(), xx2.max())

  # クラスごとにサンプルをプロット
  for idx, cl in enumerate(np.unique(y)):
    plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.6, color=cmap(idx), marker=markers[idx], label=cl)

  # テストサンプルを目立たせる（黒で描画）
  if test_idx:
    X_test, y_test = X[test_idx, :], y[test_idx]
    plt.scatter(X_test[:, 0], X_test[:, 1], color=(0, 0, 0), alpha=0.6, linewidths=1, marker='o', s=55, label='test set')

この関数で、
トレーニングデータとテストデータをプロットします。

以下のコードで、実際に描画します。

ipynb

# トレーニングデータとテストデータの特徴量を行方向に結合
X_combined_std = np.vstack((X_train_std, X_test_std))
# トレーニングデータとテストデータのクラスラベルを結合
y_combined = np.hstack((y_train, y_test))

# 決定境界をプロット
plot_decision_regions(X_combined_std, y_combined, classifier=lr, test_idx=range(105, 150))

plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

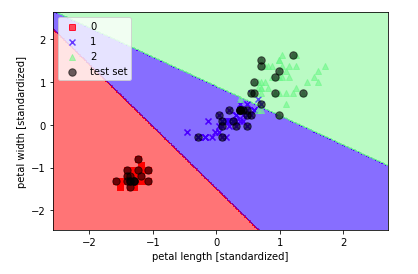
これを実行すると、以下の図ような出力が得られるはずです。

テストデータは黒色でプロットしており、
微妙に分類できていないサンプルも存在しますが、
ある程度は学習できていそうです。

以下のコードで実際のクラスを予測してみます。

ipynb

print(lr.predict_proba(X_test_std[0, :].reshape(1, -1)))
# [[4.57718485e-05 4.30250370e-02 9.56929191e-01]]

これは、テストデータの先頭のサンプルに対して、
Iris-Virginica である確率が 95.7% であることを示しています。
（クラス2: Iris-Virginica の値が最も高い）

ここまで理論を数式で理解しようと試みました。
今回メインで使用したPython機械学習の本では、
理論のさわりしか取り扱っておらず、数式の導出が意外にも省略されていたため、
分野をまたいで調べる必要がありました。

• 追加で正則化についても述べたい。
• 数式のTex入力疲れる。

まとめ

以下に今回のまとめを記載します。

• ロジスティック回帰は産業界で広く利用されている分類アルゴリズムの一つ。
• ロジット関数の逆関数がロジスティック関数。
• クラスの所属関係の確率を出力。

次回は CNN かサポートベクトルマシンを取り扱う予定です。

参考文献

• ロジット関数とロジスティック関数
• 1からみなおす線形モデル (2) - 一般化線形モデル
• 一般化線形モデル
• ロジスティック関数とシグモイド関数
• Sebastian Raschka (2015). Python Machine Learning-1st Edition, Packt Publishing. (セバスチャン・ラシュカ, 株式会社クイープ(訳) (2016). Python機械学習プログラミング達人データサイエンティストによる理論と実践, 株式会社インプレス, pp.54-66)
• Qiitaの数式チートシート
• Qiitaでの数式記述のベクトル表記
• ロジスティック回帰
• Python Machine Learning - Code Examples