はじめに

オンライン機械学習講義の予習用。(2021/04/11現在)

Python機械学習プログラミング
達人データサイエンティストによる理論と実践
の以下を取り扱います。

第3章分類問題 (3.1-3.2)

ここでは、sklearn を使ってパーセプトロンの学習を実装します。
対象データはIris データセットです。

開発環境

MacBook Air 2017
macOS Catalina 10.15.16

Google Colaboratory
sklearn 0.22.2.post1

万能な分類器は存在しない

まず前提として、学習アルゴリズムにはそれぞれ癖があるため、
解決したい問題に合わせて
モデルを変えていく必要があります。

どんな問題にも通用する万能な手法は存在しないということです。
モデルの性質を見極め、パラメータを調整しなければ、
期待する結果は得られません。

学習モデルの特徴を捉えるためには、
実験を通した練習が最も効率的です。

はじめは単純なモデルである
パーセプトロンに着目して話を進めていきます。

以下を colab notebook に入力して
sklearn のバージョンを確認します。

ipynb

import sklearn
print(sklearn.__version__) # 0.22.2.post1

2021/04/11現在、colab notebook ではデフォルトで
上記のバージョンが使用されるようです。

※ バージョンによっては、これより下のコードの整合性が取れないことがあるかもしれません。

Irisデータをロード

続いて、以下のコードで学習に必要なデータをロードし、
X に特徴量、y にラベルを格納します。

ipynb

from sklearn import datasets
import numpy as np

iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 2: petal length, 3: petal width
y = iris.target

ちなみに今回はデータをグラフにプロットしたいので、
考慮する特徴量は、
花びらの長さ（petal length）と
花びらの幅（petal width）のみになります。

続いて、どんなラベルが割り振られているのか気になるので、
以下を実行します。

ipynb


print("Class labels: ", np.unique(y)) # [0 1 2]

普通、ラベルは人間にとって分かりやすい
名前がついているはずですが、
すでにクラスラベルとして整数に変換されていたようです。

Iris-Setosa: 0, Iris-Versicolor: 1, Iris-Virginica: 2
として、与えられているということです。

パーセプトロンの学習

次にモデルの汎化性能を確保するために、
データ全体から
トレーニングデータセットとテストデータセットに
分割します。

以下のコードで、
テストデータの割合を30%（45個のサンプル）に指定します。

ipynb

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)

続いて特徴量のスケーリングを行います。

各特徴量の取りうる値を揃えるために、
StandardScalerを使います。

以下のコードで、標準化できます。

ipynb


from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
# fitメソッドで平均と標準偏差を計算
sc.fit(X_train)
X_train_std = sc.transform(X_train) # transformメソッドで標準化
X_test_std = sc.transform(X_test)

StandardScalerのfitメソッドでを使うと
特徴量ごとの平均 μ と標準偏差 σ を計算できます。

これらのパラメータを使い、
transform メソッドでトレーニングデータを標準化します。

テストデータにも
同じスケーリングパラメータを適用したのは、
相互の基準を揃え、比較できるようにするためです。

これでパーセプトロンをトレーニングできる状態になりました。

以下のコードで、
パーセプトロンのインスタンスを作成し、
トレーニングを実行します。

ipynb


from sklearn.linear_model import Perceptron

# エポック40, 学習率0.1のパーセプトロンインスタンスを作成
ppn = Perceptron(max_iter=40, eta0=0.1, random_state=0, shuffle=True)
# トレーニングデータをモデルに適合させる
ppn.fit(X_train_std, y_train)

※ インスタンスを作成するときにエポックと学習率を定義します。

次に予測を行います。
以下の predict メソッドで予測を実行し、
誤分類されたサンプルも表示します。

ipynb


# テストデータで予測を実施
y_pred = ppn.predict(X_test_std)
# 誤分類のサンプル個数を表示
print("Missclassified samples: {}".format((y_test != y_pred).sum()))

# Missclassified samples: 5

せっかく表示した結果ですが、
一般に、機械学習で推奨される報告は、
モデルの誤分類率ではなく、正解率です。
そのため、誤分類を出して終わりではないのです。

以下のコードで、
正解率を計算します。

ipynb


# 実装された性能指標を使用
# ここではパーセプトロンの正解率を計算
from sklearn.metrics import accuracy_score

print("Acuracy: {:.2f}".format(accuracy_score(y_test, y_pred)))

ちなみに正解率は以下の式で定義されています。

正解率 = 1 - 誤分類率

テストデータの誤分類率は 5/45=0.111...
なので、上記の式に当てはめると、

正解率 = 1 - 0.11 = 89%

になります。

このようにして、学習済みのモデルを評価します。

※ 今回は簡単な解析だったため、
過学習を防止する手法等は適用していないことに注意。

学習結果の可視化

続いて、
トレーニングしたモデルを可視化します。

モデルの決定領域をプロットし、
未知のデータに対してその程度識別できるか見ていきます。

以下のコードで、描画の定義をします。

ipynb


from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt

def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
  # マーカーとカラーマップの準備
  markers = ('s', 'x', '^', 'v')
  colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
  cmap = ListedColormap(colors[:len(np.unique(y))])

  # 決定領域のプロット
  x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
  x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1

  # グリッドポイントの生成
  xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                                      np.arange(x2_min, x2_max, resolution))

  # 各特徴量を1次元配列に変換して予測を実行
  Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
  # 予測結果を元にグリッドポイントのデータサイズに変換
  Z = Z.reshape(xx1.shape)
  # グリッドポイントの等高線をプロット
  plt.contourf(xx1, xx2, Z, alpha=0.5, cmap=cmap)
  # 軸の範囲を設定
  plt.xlim(xx1.min(), xx1.max())
  plt.ylim(xx2.min(), xx2.max())

  # クラスごとにサンプルをプロット
  for idx, cl in enumerate(np.unique(y)):
    plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.6, color=cmap(idx), marker=markers[idx], label=cl)

  # テストサンプルを目立たせる（黒で描画）
  if test_idx:
    X_test, y_test = X[test_idx, :], y[test_idx]
    plt.scatter(X_test[:, 0], X_test[:, 1], color=(0, 0, 0), alpha=0.6, linewidths=1, marker='o', s=55, label='test set')
    # 誤分類されたサンプルは黄色でプロット
    plt.scatter(X_test[y_test != y_pred, 0], X_test[y_test != y_pred, 1], color=(1, 1, 0), alpha=0.6, linewidths=1, marker='o', s=55, label='Missclassified')

この関数で、
トレーニングデータとテストデータをプロットします。

下の方にある、
「# 誤分類されたサンプルは黄色でプロット」以下が
誤分類されたサンプルを描画するためのコードです。

以下のコードで、実際に描画してみましょう。

ipynb


# トレーニングデータとテストデータを行方向に結合
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
# 決定境界のプロット
plot_decision_regions(X=X_combined_std, y=y_combined, classifier=ppn, test_idx=range(105, 150))

plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.show()

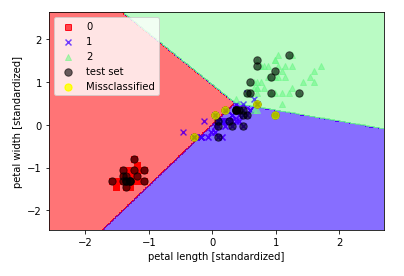
これを実行すると、以下の図ような出力が得られるはずです。

テストデータは黒色でプロットしており、
その中でも誤分類したものは黄色になっているはずです。

この結果から、
パーセプトロンアルゴリズムでは
Irisデータセットの3つの品種を線形の決定境界では
完全に区切ることができないことが分かります。

一般に、
パーセプトロンアルゴリズムがデータ解析で使用されないのは、
完全な線形分離が要求されるからです。
この条件を満たさない限り、
パーセプトロンアルゴリズムは収束しないため、
期待する結果は得られません。

まとめ

以下に今回のまとめを記載します。

実験を通して、特定の問題に最適なモデルを選択する。
誤分類率ではなく正解率を報告する。
クラスラベルは整数に変換して使用する。
パーセプトロンアルゴリズムは線形分離が不可能だと収束しない。

次回はクラスが完全に線形分離できない場合であっても、
コスト関数が最小値に収束するロジスティック回帰を取り上げます。

参考文献

ImportError: No module named 'sklearn.cross_validation'の対処
sklearn.linear_model.Perceptron のパラメータから n_iter が削除されてた件のメモ
Sebastian Raschka (2015). Python Machine Learning-1st Edition, Packt Publishing. (セバスチャン・ラシュカ, 株式会社クイープ(訳) (2016). Python機械学習プログラミング達人データサイエンティストによる理論と実践, 株式会社インプレス, pp.48-53)

Python機械学習プログラミング備忘録 3.1-3.2

はじめに

目次

開発環境

万能な分類器は存在しない

Irisデータをロード

パーセプトロンの学習

学習結果の可視化

まとめ

参考文献