LoginSignup
3
3

More than 3 years have passed since last update.

機械学習工学／MLSEAdvent Calendar 2019Day 4
@soup01

機械学習#k近傍法とその実装とその色々

Posted at

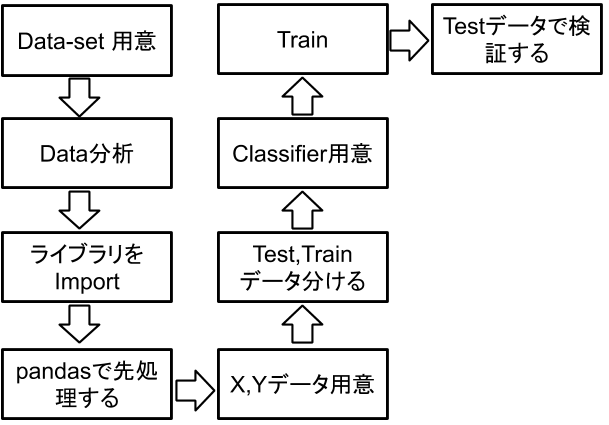
前書き

この記事はSentdexさま、偉大なプログラマーのVideoを勉強しながらとったメモです。
https://www.youtube.com/user/sentdex

まず、K-NNはなんですか？WIKIによりますと：
https://ja.wikipedia.org/wiki/K%E8%BF%91%E5%82%8D%E6%B3%95

k近傍法は、ほぼあらゆる機械学習アルゴリズムの中で最も単純である。あるオブジェクトの分類は、その近傍のオブジェクト群の投票によって決定される（すなわち、k 個の最近傍のオブジェクト群で最も一般的なクラスをそのオブジェクトに割り当てる）。k は正の整数で、一般に小さい。k = 1 なら、最近傍のオブジェクトと同じクラスに分類されるだけである。二項分類の場合、k を奇数にすると同票数で分類できなくなる問題を避けることができる。

うん、すごく民主的なやり方。まず下のグラフをみてください。6点のデータがありますね。
もしあなたがグループ分けするなら、どうしましょう。
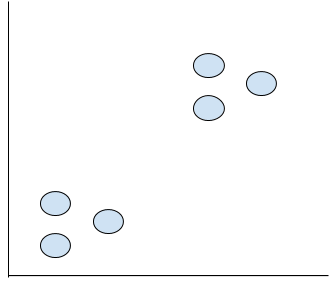
image.png

多分こうになりますね。ではなぜですか？だってお互いの距離が近いですもの。
私達やってのは”Cluster”と言います。
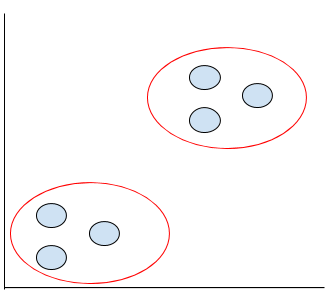
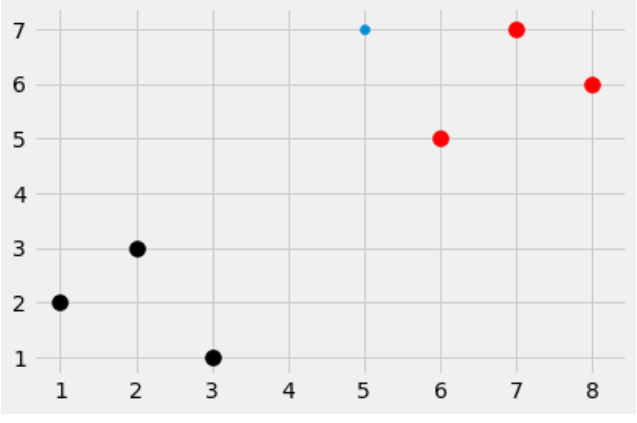
image.png

よろしい。今度は＋とー、既にグループ分けしたものがあります。
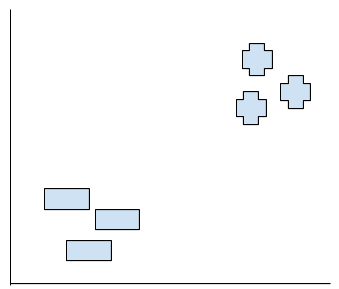
image.png

いま赤点がでできました。さ、この赤点はどっちのグループに入るでしょうか？
恐らく＋のグループに入るでしょう。でもなぜ？頭の中にどんな思考回路で考えたですか？
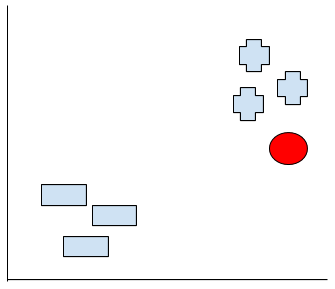
image.png

今度の赤点は恐らく－グループに入るでしょう。またなんぜですか？
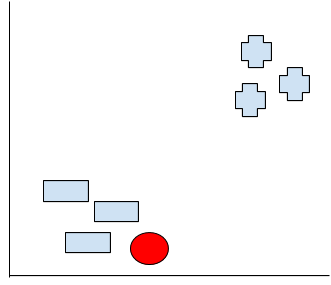
image.png

最後もし赤点ここにいるなら、どっちのグループなんでしょうか？
これはあなた選んでるアルゴリズムによります。
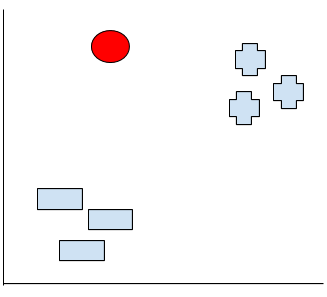
image.png

さ、話戻りましょう。多分（少なくても私が）はこの赤点はーのグループより＋のグループのほうが距離近いから赤点が＋グループです！と判断してたはずです。
そして私たちこの”考え”をK-nearest neighbors(K-NN)と呼びます。
日本語だとk近傍法だと、思います。
K-NNやってる仕事はグループ分けしたいポイントをと他のポイントの距離を測り、どっちのグループに入るのかを判断するだけです。先みせた例ではグループは２しかないですが、もし課題が１００があるとしたら？もし課題１０００があるとしたら？うん、気を失いちゃいそう…
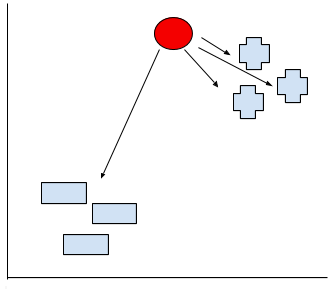
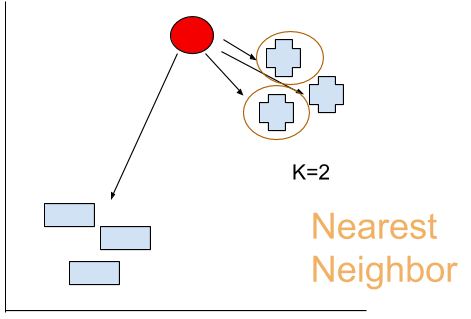
image.png

ですが、よく考えてください。本当にすべてのポイントも測らないといけないでしょうか？大体の場合は必要がないと思います。K-NNには”K"を定義するのです。じゃ、仮にK=2を設定しましょう。
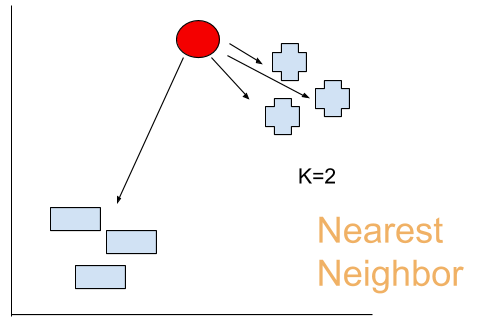
image.png

うんうん、なるほど。多分オレンジ丸しる書いてるのところは赤点に一番近いだね。
だから、私はこの赤点が＋グループと、判断します。
image.png

今度黒点が出てきました。K=2の場合、一番近いの点はどっちでしょうか？
うん、多分この２つですね。問題出ました！引き分けになった！それじゃ判断できません。
K-NNは基本的に、このkは偶数しちゃだめです。
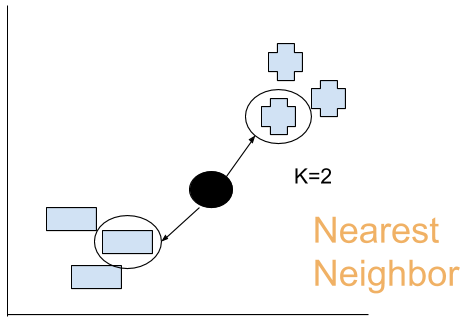
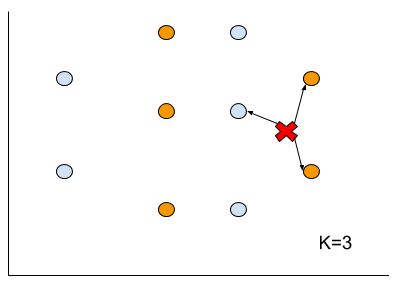
image.png

なので、K=3を設定します。K=3になると私たちもう一つの点が必要になります。
多分…ーのほうが近いかな？
この黒点がーのグループだと。
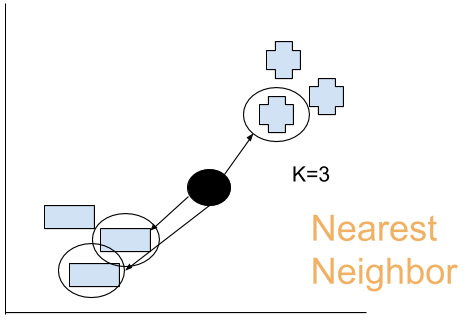
image.png

で、先の判断だとーが２つ、＋が１つ。２/３＝６６％
この６６％はこの判断に対するconfidence（信頼度）です。
そして先測った距離のこと、Euclidean Distanceだと言います。

実装

まず流れを決めましょう。
image.png

データ用意

ではsklearnを使って実装しましょう。

まずData-setを用意しなといけないので、今回使うのはこれです：
https://archive.ics.uci.edu/ml/datasets/breast+cancer+wisconsin+%28original%29
乳がんに関するデータです。

データ分析

ダウンロードされたものはこうなると思います。
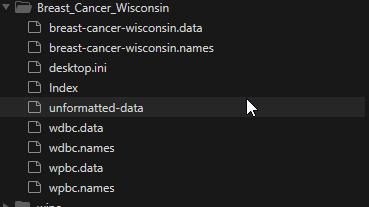
image.png

breast-cancer-wisconsin.namesを開くとデータに関する説明が書いております。
7.のところに各データ値の”意味”が書いています。ここからみると1から10番まではFeaturesで11はLabelだそうですね。
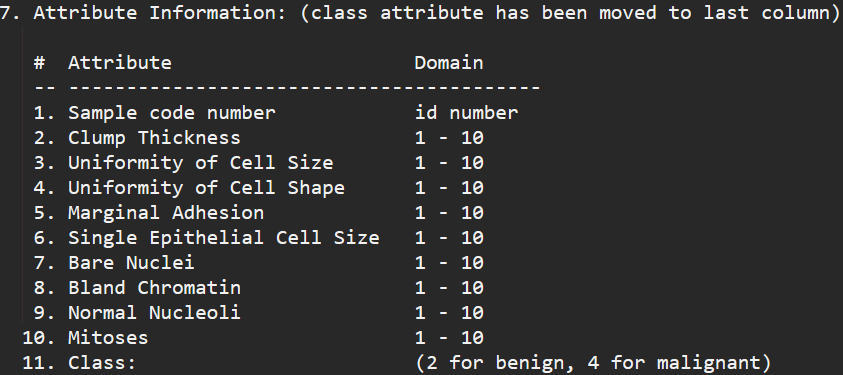
image.png
breast-cancer-wisconsin.dataにデータが入っています。ですが肝心なラベルが書いてません。
image.png
プログラムで追加でもできますが、いまはとりあえず手で入力します…
image.png

ライブラリImport


import numpy as np
from sklearn import preprocessing,model_selection,neighbors
import pandas as pd

pandasで先処理する

idはData-setの中にあまり関係がなさそうなのでDropします。
breast-cancer-wisconsin.namesの中に抜けたところは”？”を表示すると書いています。
NANは基本NGなのでここで仮に－99999に置き換えます。

df=pd.read_csv('Data/Breast_Cancer_Wisconsin/breast-cancer-wisconsin.data')
df.replace('?',-99999,inplace=True)
df.drop(['id'],1,inplace=True)

X,Yデータ用意する

簡単にいうと、Xはラベル入ってないデータ。Yはラベルだけのデータ。
だからXは”class”がDropされたDataFrameを入れます。
Yは”Class"だけのDataFrameを入れます。

#features
x=np.array(df.drop(['class'],1))
#label
y=np.array(df['class'])

Test,Trainデータ分ける

80%のTrainデータと20%のテストデータが分けます。

x_train,x_test,y_train,y_test=model_selection.train_test_split(x,y,test_size=0.2)

Classifier用意する

K-NN使うから当然KNeighborsClassifierですね。

clf=neighbors.KNeighborsClassifier()

Train

clf.fit(x_train,y_train)

Testデータで検証する

うん～大体96%くらいかな。まぁまぁいい精度ですね。

accuracy=clf.score(x_test,y_test)
print(accuracy)

>0.9642857142857143

全体Code

import numpy as np
from sklearn import preprocessing,model_selection,neighbors
import pandas as pd

df=pd.read_csv('Data/Breast_Cancer_Wisconsin/breast-cancer-wisconsin.data')
df.replace('?',-99999,inplace=True)
df.drop(['id'],1,inplace=True)

#features
x=np.array(df.drop(['class'],1))
#label
y=np.array(df['class'])

x_train,x_test,y_train,y_test=model_selection.train_test_split(x,y,test_size=0.2)
clf=neighbors.KNeighborsClassifier()
clf.fit(x_train,y_train)
accuracy=clf.score(x_test,y_test)
print(accuracy)

深く掘りましょう

いまからsklearn頼れずに自力でKNNを書いてみます。
まずもう一度見ていきましょう。実際判黒点をどっちのグループにするのかを判断するには距離ですよね。
この距離私達”Euclidean Distance”と言います。
image.png

計算式

計算式はこうになります。字が醜いすいません…
ここで、
i＝Diemensions
q＝点
p＝違う点
image.png

例えばq=(1,3)、p=(2,5)。
Euclidean Distance＝2.236
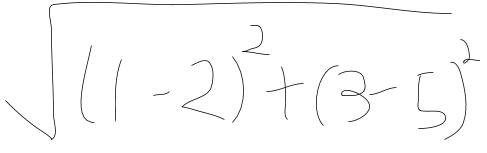
image.png

実装

では、まずこの数式をpythonで書きましょう。

from math import sqrt

plot1=[1,3]
plot2=[2,5]

euclidean_distance=sqrt( (plot1[0]-plot2[0])**2 + (plot1[1]-plot2[1])**2 )

print(euclidean_distance)

Functionを作る

Functionを作る前にまず思想を考えましょう。
以下のコードはまずDatasetと新しいデータをPlotしてみます。
Functionの機能は、そうですね。
data:Train_dataだね。
predict:こっちはTest_dataだね。
k:何点を取るのか、たしかにsklearnにはDefaultでk＝5と気がします…
そして最後はなにかの魔法を起動させて結果出してくれる！

実装

from math import sqrt
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
from collections import Counter
import warnings

style.use('fivethirtyeight')

data_set={'k':[[1,2],[2,3],[3,1]]
          ,'r':[[6,5],[7,7],[8,6]]} 

new_features=[5,7]

[[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in data_set[i]] for i in data_set]
plt.scatter(new_features[0],new_features[1])

def k_nearest_neighbors(data,predict,k=3):
    if len(data) >=k:
        warnings.warnings('K is set to a value less than total voting groups!')

    #?make some magic

    return vote_result

image.png

魔法の仕掛を考える

実際このFunctionはなにか求めてるのか？
私達どうやって一つのData-pointと他のData-pointを比べ、そして一番近いPointを探します。
KNNにはPredictのPointをすべてのPointに比べないといけない、それはKNNの問題です。
確かに、Radiusを設定しある程度のPointしかみないという手法で計算の時間を節約することも、可能です。

実装

  1. For Loopの中に全てのeuclidean_distaneを計算し、配列に追加します。
  2. たとえば[2.44,'r'],[1.4,'r'],[2.14,'k'],[4.4,'k'],[5.44,'k']..のように。
  3. そしてvotesという配列を、先の配列に計算されたeuclidean_distane小さいから多きまでソートします。
  4. そのeuclidean_distaneに対応するラベルを格納します。
  5. Counter(votes).most_common(1)を使って一番頻度高い元素を取り出します。ここは仮に[('r', 3)]。
  6. Counter(votes).most_common(1)[0][0]を使うことによって、’ｒ’が更に取り出せます。
  7. 最後は結果をReturnします。
from math import sqrt
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
from collections import Counter
import warnings

style.use('fivethirtyeight')

data_set={'k':[[1,2],[2,3],[3,1]]
          ,'r':[[6,5],[7,7],[8,6]]} 

new_features=[5,7]

[[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in data_set[i]] for i in data_set]
plt.scatter(new_features[0],new_features[1])

def k_nearest_neighbors(data,predict,k=3):
    if len(data) >=k:
        warnings.warnings('K is set to a value less than total voting groups!')

    for group in data:
        #data_set={'k':[[1,2],[2,3],[3,1]],'r':[[6,5],[7,7],[8,6]]} 
        #iterating  ^                       ^
        for features in data[group]:
            #data_set={'k':[[1,2],[2,3],[3,1]],'r':[[6,5],[7,7],[8,6]]} 
            #iterating      ^^^^^^^^^^^^^^^^^      ^^^^^^^^^^^^^^^^^

            #not fast and just for 2-dimensions
            #euclidean_distacnce=sqrt(  (features[0]-predict[0])**2 + features[1]-predict[1]**2 )

            #better
            #euclidean_distane=np.sqrt( np.sum((np.array(features)-np.array(predict))**2))

            euclidean_distane=np.linalg.norm( np.array(features)-np.array(predict)  )
            distance.append([euclidean_distane,group])

    votes=[i[1] for i in sorted(distance)[:k]]

    print(Counter(votes).most_common(1))

    vote_result=Counter(votes).most_common(1)[0][0]

    return vote_result

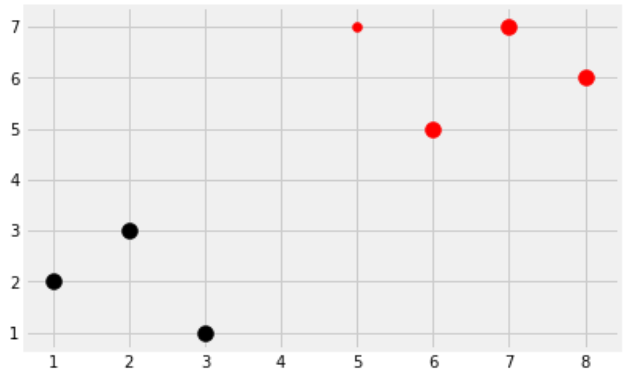
result=k_nearest_neighbors(data_set,new_features,k=3)
print(result)
[[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in data_set[i]] for i in data_set]
plt.scatter(new_features[0],new_features[1],color=result)

うん、赤組だね！
image.png

もう少し先に進もう

今度は本物のデータを使って、scikit-learnとどっちか精度高いかを比べて見ましょう。
1. full_data=df.astype(float).values.tolist()でDataの順をランダムに入れ替えます。
2. train_setとtest_setのData-setを用意します。辞書で2と4で先の乳がんのデータにあるClassに合わせます。
3. train_data=full_data[:-int(test_size*len(full_data))]、例えばfull_dataが100個あれば、test_sizeは0.2なので、100＊0.2＝20になります。train_data=full_data[:-20]は80個のデータセットがtrain_data格納します。
4. test_data=full_data[-int(test_size*len(full_data)):]、例えばfull_dataが100個あれば、test_sizeは0.2なので、100＊0.2＝20になります。train_data=full_data[-20:]は最後の20個データセットがtest_data格納します。
5. 最後のFor loopはTrain_dataとtest_setを使って、test_setはグループ2なのに、voteが4帰ってきたら間違えたと言えますし、逆にtest_setはグループ2で、voteが4帰ってきたら正しいとわかり、correctを＋１にします。そして正確数/Totalは正解率に言えます。

自力Function

from math import sqrt
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
from collections import Counter
import warnings
import pandas as pd
import random

style.use('fivethirtyeight')

def k_nearest_neighbors(data,predict,k=3):
    if len(data) >=k:
        warnings.warnings('K is set to a value less than total voting groups!')

    for group in data:
        #data_set={'k':[[1,2],[2,3],[3,1]],'r':[[6,5],[7,7],[8,6]]} 
        #iterating  ^                       ^
        for features in data[group]:
            #data_set={'k':[[1,2],[2,3],[3,1]],'r':[[6,5],[7,7],[8,6]]} 
            #iterating      ^^^^^^^^^^^^^^^^^      ^^^^^^^^^^^^^^^^^

            #not fast and just for 2-dimensions
            #euclidean_distacnce=sqrt(  (features[0]-predict[0])**2 + features[1]-predict[1]**2 )

            #better
            #euclidean_distane=np.sqrt( np.sum((np.array(features)-np.array(predict))**2))

            euclidean_distane=np.linalg.norm( np.array(features)-np.array(predict)  )
            distance.append([euclidean_distane,group])

    votes=[i[1] for i in sorted(distance)[:k]]

    print(Counter(votes).most_common(1))

    vote_result=Counter(votes).most_common(1)[0][0]

    return vote_result

df=pd.read_csv('Data/Breast_Cancer_Wisconsin/breast-cancer-wisconsin.data')
df.replace('?',-99999,inplace=True)
df.drop(['id'],1,inplace=True)
full_data=df.astype(float).values.tolist()

#random sort your data
random.shuffle(full_data)

test_size=0.2
train_set={2:[],4:[]}
test_set={2:[],4:[]}

train_data=full_data[:-int(test_size*len(full_data))]#first 80%
test_data=full_data[-int(test_size*len(full_data)):] #last 20%

'''
for i in train_data:
    #train_set[i[-1]] is the class data from train_set:2 or 4.
    #.append(i[:-1]) is the function to take all the data (unless the class) to the list 
    train_set[i[-1]].append(i[:-1])

for i in test_data:
    test_set[i[-1]].append(i[:-1])
'''
correct=0
total=0

for group in test_set:
    #loop the class'2' and '4'
    for data in test_set[group]:
        #take the data from set'2' and '4'
        vote=k_nearest_neighbors(train_set,data,k=5)
        if group == vote:
            correct+=1
        total+=1


print('Accuracy:',correct/total)

>Accuracy: 0.9640287769784173

sklearn Function

いつも通りのコード。

import numpy as np
from sklearn import preprocessing,model_selection,neighbors
import pandas as pd

df=pd.read_csv('Data/Breast_Cancer_Wisconsin/breast-cancer-wisconsin.data')
df.replace('?',-99999,inplace=True)

df.drop(['id'],1,inplace=True)

#features
x=np.array(df.drop(['class'],1))
#label
y=np.array(df['class'])

x_train,x_test,y_train,y_test=model_selection.train_test_split(x,y,test_size=0.4)

clf=neighbors.KNeighborsClassifier()
clf.fit(x_train,y_train)

accuracy=clf.score(x_test,y_test)

>Accuracies: 0.9671428571428571

結論

…正解率あまり変わらないですが、計算Speedは明らかにsklearnの方が早いです。

最後に

うんーKNNを使わずに分類できる方法他にはまだたくさんあると思います。
例えばこういうLinear的なデータがあるとしましょう。
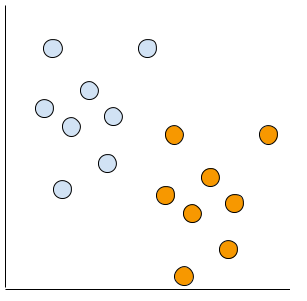
image.png
多分？こういう線を先に書いておいて…
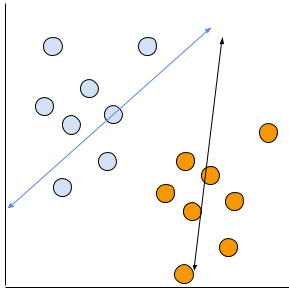
image.png
そして新しい赤点が出てきます。
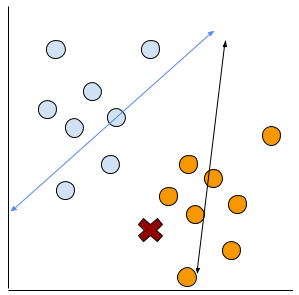
image.png
Square Errorでなんらかの計算でもいけるのかな？
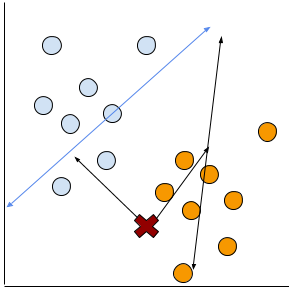
image.png
今度はこのようなNon-linearデータがあるとしよう。
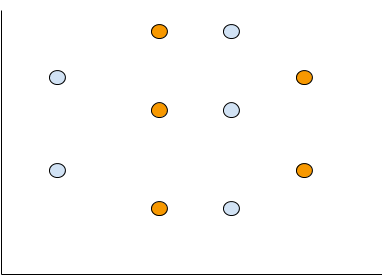
image.png
無理やり線を引くのなら、多分こんな感じかな？
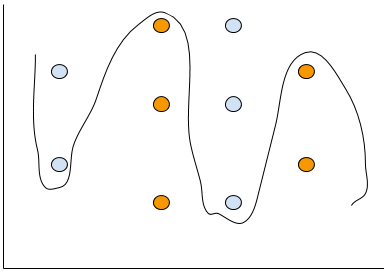
image.png
そういう場合はKNNを使えばすぐわかるじゃないかな？
image.png

やっばり難しいねー
最後まで付き合って頂いてありがとうございます！
またよろしくおねがいします！

3
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
3