前回線形回帰の仕組みを数式を用いて説明しました。今回は線形回帰と並んで最も基本的な機械学習アルゴリズムの一つであるロジスティック回帰(Logistic Regression)について、モデルの仕組みを数式を用いて説明します。
前提知識
- 機械学習の基礎知識
- 用語とかプロセスとか
- 学部1年程度の線形代数と解析学
- 線形代数の方は行列の積と転置を使います
- 解析学の方は偏微分や勾配を使います
参考資料
- Aurelien Geron "Hands-on Machine Learning with Scikit-Learn & Tensorflow"
- モデルの原理の説明や数式の一部を参考にしました。
ロジスティック回帰とは何か?
学習データと予測すべき値の正解が与えらえて、それらの間の関係を学習することを教師あり学習といいます。教師あり学習は主に2つに分類できて、「回帰」と「分類」に分けることができます。
回帰は数値を予測する問題です。例えば地域の人口や平均年収から土地の価格を予測する問題では、予測する対象は数値なので、回帰問題に分類されます。
一方分類は種類を予測する問題です。もっとも有名なのは、スミレ(iris)の種類を花びら(petal)と萼片(sepal)の長さと幅で分類する問題ですね。
前回説明した線形回帰は回帰問題を解くアルゴリズムです。一方でロジスティック回帰は「回帰」という名前がついていますが、実は分類問題を解くためのアルゴリズムです。なんて紛らわしい名前を付けるんだ!と思うかもしれませんが、これから説明するようにロジスティック回帰が予測しているのは実は確率であり、確率は数値なので、あながち間違いではありません。
分類問題はさらに「二値分類」と「多クラス分類」に分けることができます。二値分類は与えられたデータを2つのクラス(種類)に分ける問題で、多クラス分類はそれ以上のクラスに分ける問題です。
実はロジスティック回帰で直接解けるのは二値分類問題だけです。それではあまり使い物にならないと思うかもしれませんが、OvR (One vs Rest) やOvO (One vs One) などの一般的な手法を使うと多クラス分類を二値分類に帰着させることができるので、ロジスティック回帰でも解けるようになります。また、ロジスティック回帰を多クラスを直接扱えるように拡張した多項ロジスティック回帰(ソフトマックス回帰)というアルゴリズムもあります。これについてはまた記事を書くと思います。
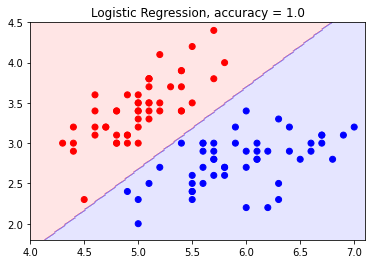
実際にどのように分類が行われるのかを可視化したのが下図です。
これはスミレの種類を分類しています。横軸は萼片の長さ、縦軸は萼片の幅です。赤い点はSetosaという種類のスミレで、青い点はVersicolorという種類のスミレです。ロジスティック回帰はここに直線を引くことでスミレの種類を分類し、直線の上側ならSetosa、下ならVersicolorというように分類します。この分類は未知のデータに対して適用することができて、種類がわからないスミレの萼片の長さと幅を計測してこの図にプロットし、その点が赤い領域にあったらそれはSetosa、青い領域にあったらVersicolorという風に種類を予測することができます。
定式化
それでは、ロジスティック回帰がどのように二値分類問題を解くのかを見ていきます。分類するクラスをクラス0とクラス1と呼ぶことにします。ロジスティック回帰は、与えられたデータがクラス1に属する確率を予測します。もし確率が0.5以上であればそのデータはクラス1に属し、0.5未満であればクラス0に属すると判断されます。
確率がどのように計算されるのか見ていきましょう。ロジスティック回帰は線形回帰と同様に、特徴量の1次式を用いて予測を行います。特徴量というのはデータを表す値の集まりで、例えばirisの分類の例でいうと、花びらと萼片の長さと幅が特徴量になります。特徴量を$x_1, x_2, \dots, x_n$とすると、特徴量の1次式は次式で表されます。
\theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_n x_n
ここで係数$\theta_i$はまだわかっていません。ベクトルを使うとこの式は$\boldsymbol{\theta}^T \boldsymbol{x}$と短く表すことができます。$\boldsymbol{x}$はバイアス項を含むことに注意してください。バイアス項は前回の記事で説明しています。あと$\boldsymbol{\theta}$の右肩の$T$は、ベクトルの内積を行列の積として表すために行ベクトルを列ベクトルに変形しています。
線形回帰では、この式の値を直接予測値として扱っていましたが、今回予測したいのは確率なのでそうはいきません。確率は0から1の範囲に収まる必要があるからです。そこで、ロジスティック回帰ではこの値を0から1の範囲に直すことを考えます。ここで登場するのがシグモイド関数です。
シグモイド関数は次の式で定義されます。
\sigma(t) = \frac{1}{1 + \exp (-t)}
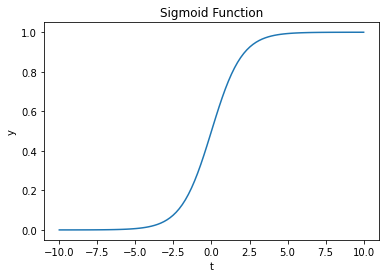
この関数のグラフを描くと次のようになります。
関数の値が0から1の範囲に収まっていることがわかりますね。$t$の値が大きいと関数の値は1に近く、$t$の値が小さいと関数の値は0に近くなります。$t=0$の周りではなめらかに変化しています。この曲線はロジスティック曲線とも呼ばれ、一般にS字カーブと呼ばれているやつです。
このシグモイド関数をつかって$\boldsymbol{\theta}^T \boldsymbol{x}$を0から1の範囲に直したものが、確率の予測値$\hat{p}$となります。つまり、
\hat{p} = \sigma (\boldsymbol{\theta}^T \boldsymbol{x})
となります。$\boldsymbol{\theta}^T \boldsymbol{x}(=\log \frac{\hat{p}}{1 - \hat{p}})$をロジット(logit)と呼びます。
コスト関数
パラメータ$\boldsymbol{\theta}$が変わると、$\hat{p}$も変化します。パラメータの良さを測るために、線形回帰のときと同様にコスト関数を導入します。これは予測が真の値からどれだけ離れているかを表す関数で、コスト関数の値が大きいほどパラメータが悪く、小さいほどパラメータが良いことになります。そしてコスト関数の値ができるだけ小さくなるようなパラメータを探していけばよいことになります。
まず一つのインスタンスに対するコスト関数を次式で定義します。
c(\boldsymbol{\theta}) = \begin{cases}
-\log (\hat{p}) & \text{if } y = 1 \\
-\log (1 - \hat{p}) & \text{if } y = 0
\end{cases}
$y$というのはそのインスタンスの正しいクラスを表しています。$y = 1$のときは確率$\hat{p}$が大きく出てほしいので、$\hat{p}$が小さいほどコスト関数が大きくなるように定めればよいです。$-\log (\hat{p})$は$\hat{p}$が小さくなると急激に増加するので、この条件を満たしています。一方$y = 0$のときは逆に$\hat{p}$が小さく出てほしいので、$-\log (1 - \hat{p})$をコストとすることで大きい$\hat{p}$を罰することができます。
ここではコスト関数を場合分けで表しましたが、実はこれは一つの式で表すことができて、
c(\boldsymbol{\theta}) = -\left(y \log (\hat{p}) + (1 - y)\log (1 - \hat{p})\right)
となります。$y=1$のときは第2項が0になり、$y=0$のときは第1項が0になるので、場合分けで表したコスト関数と一致することがわかります。
データ全体に対するコスト関数は、単に上で定義したコスト関数のすべてのインスタンスについての和とします。インスタンスの数を$m$とすると、
J(\theta) = -\sum_{i=1}^m \left(y^{(i)} \log (\hat{p}^{(i)}) + (1 - y^{(i)})\log (1 - \hat{p}^{(i)})\right)
右肩の$(i)$は「$i$番目の」という意味です。このコスト関数は**ログ損失(log loss)**と呼ばれます。
パラメータの決定
コスト関数の偏微分を求める
このコスト関数を最小にするようなパラメータ$\boldsymbol{\theta}$を探したいです。線形回帰のときと同様に、関数の極値を求めるには微分をします。
まずコスト関数を微分しやすい形に変形します。
\begin{align}
J(\boldsymbol{\theta}) &= -\sum_{i=1}^m \left( y^{(i)} \log (\hat{p}^{(i)}) + (1-y^{(i)}) \log (1-\hat{p}^{(i)}) \right) \\
&= -\sum_{i=1}^m \left( y^{(i)} \log \left( \frac{\hat{p}^{(i)}}{1-\hat{p}^{(i)}} \right) + \log (1-\hat{p}^{(i)}) \right) \\
&= -\sum_{i=1}^m \left( y^{(i)} (\boldsymbol{\theta}^T \boldsymbol{x}^{(i)}) + \log \left( \frac{\exp (-\boldsymbol{\theta}^ T \boldsymbol{x}^{(i)})}{1+\exp (-\boldsymbol{\theta} ^ T \boldsymbol{x}^{(i)})} \right) \right) \\
&= -\sum_{i=1}^m \left( (y^{(i)} - 1) (\boldsymbol{\theta}^T \boldsymbol{x}^{(i)}) - \log (1+\exp (-\boldsymbol{\theta}^ T \boldsymbol{x}^{(i)})) \right)
\end{align}
自分で手を動かしながら、頑張って式を追ってください…。僕はこの式をLaTeXで入力するのが一番大変でした。
それではこれを微分していきましょう。コスト関数は$\boldsymbol{\theta}$の要素一つ一つを変数とする多変数関数なので、$j$番目の要素$\theta_j$で偏微分していきます。
\begin{align}
\frac{\partial}{\partial\theta_j} J(\boldsymbol{\theta}) &= - \sum_{i=1}^m \left( (y^{(i)} - 1) x^{(i)}_j + \frac{\exp (-\boldsymbol{\theta}^T \boldsymbol{x}^{(i)})}{1+\exp (-\boldsymbol{\theta}^T \boldsymbol{x}^{(i)})} x^{(i)}_j \right) \\
&= -\sum_{i=1}^m \left( y^{(i)} - \frac{1}{1+\exp (-\boldsymbol{\theta}^T \boldsymbol{x}^{(i)})} \right) x^{(i)}_j \\
&= \sum_{i=1}^m \left( \sigma (\boldsymbol{\theta}^T \boldsymbol{x}^{(i)}) - y^{(i)} \right) x^{(i)}_j
\end{align}
これは線形回帰のコスト関数の偏微分
2 \sum_{i=1}^m \left( \boldsymbol{\theta}^T \boldsymbol{x}^{(i)} - y^{(i)} \right) x^{(i)}_j
と非常によく似ています。コスト関数が全然違うのに微分が同じ形になるのは興味深いですね。
このコスト関数の偏微分はシグマを使わずに表すことができます。導出は線形回帰のときとほとんど同じなので省略します。
\frac{\partial}{\partial \theta_j} J(\boldsymbol{\theta}) = \boldsymbol{x}_j^T (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y})
新しく登場した文字だけ説明しておくと、$X$はデータ全体を表す$m \times (n+1)$行列です。$X$の行はインスタンスを表していて、列は特徴量を表しています。バイアス項を追加するので、次元が$m \times (n+1)$となることに注意してください。$X_{ij}$は$i$番目のインスタンスの$j$番目の特徴量ということになります。$\boldsymbol{x}_j$というのは$X$の$j$列目を表す列ベクトルです。$\boldsymbol{y}$は各インスタンスのクラスをまとめて表した列ベクトルで、$y_i$が$i$番目のインスタンスのクラスを表しています。また、$\sigma(X\boldsymbol{\theta})$というのは$X\boldsymbol{\theta}$(列ベクトル)の各要素に対してシグモイド関数を適用するという意味です。
勾配を求める
ここまでくれば勾配を求めるのは簡単で、
\begin{align}
\nabla J(\boldsymbol{\theta}) &= \begin{pmatrix}
\boldsymbol{x}_0^T (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y}) \\
\boldsymbol{x}_1^T (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y}) \\
\vdots \\
\boldsymbol{x}_n^T (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y})
\end{pmatrix} \\
&= \begin{pmatrix}
\boldsymbol{x}_0^T \\
\boldsymbol{x}_1^T \\
\vdots \\
\boldsymbol{x}_n^T
\end{pmatrix} (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y}) \\
&= \begin{pmatrix}
\boldsymbol{x}_0 & \boldsymbol{x}_1 & \dots & \boldsymbol{x}_n
\end{pmatrix}^T (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y}) \\
&= X^T (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y})
\end{align}
この式を線形回帰のコスト関数の勾配$2 X^T (X\boldsymbol{\theta} - \boldsymbol{y})$と見比べてみましょう。両者は全く同じ形をしていることがわかります。
コスト関数の最小値を求める
コスト関数が最小となるところでは、勾配が0になります。線形回帰のときは、勾配が0になる点を方程式を解くことで解析的に求めることができました。しかし、ロジスティック回帰の場合はそれができません。つまり、
X^T (\sigma(X\boldsymbol{\theta}) - \boldsymbol{y}) = 0
の解を閉じた式で表すことはできないのです。それでは、どうやってコスト関数の最小値を求めるのでしょうか?
ここで、勾配が何を表しているのかを思い出してみましょう。勾配は、関数の傾きが最も大きくなる方向を指し示しているベクトルでした。なので、勾配が指し示す向きに進んでいけば、ちょうど山を登るように関数の値は上昇していきます。逆に、勾配の逆向きに進んでいけば関数の値は減少していき、いつか谷底つまり極小値に到達します。このように勾配を下っていくことで関数の極小値を求める方法を**最急降下法(Gradient descent)**といいます。
ここで注意しておかなければいけないことは、この方法で求めた極小値は局所最適解であり、大域最適解、つまり関数全体での最小値になるとは限らないということです。山や谷がいくつもあるような関数では、最急降下法で谷底まで行くことができますが、それが一番低い谷であるとは限らないということです。
しかし、ロジスティック回帰のコスト関数は凸関数、つまり谷が1つしかないことがわかっているので、最急降下法で最適解を求めることができることが保証されています。このことの証明は、以下の記事がとても分かりやすかったです。
最急降下法ではまず、初期解$\boldsymbol{\theta}_0$を決めます。これはランダムに決めて大丈夫です。そして、解を以下の漸化式で更新していきます。
\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_k - \eta \nabla J(\boldsymbol{\theta}_k)
この式は今ある解の勾配の逆方向に進んでいくということを表しています。$\eta$は**学習率(Learning rate)**と呼ばれます。$\eta$が大きすぎると谷底を飛び越えてしまいますが、小さすぎるといつまでも収束しません。適度な大きさに決める必要があります。
最急降下法を十分なステップ繰り返すことで、最適なパラメータの近似解$\boldsymbol{\theta}$を求めることができます!
実装例
import numpy as np
from sklearn.base import BaseEstimator, ClassifierMixin
class MyLogisticRegression(BaseEstimator, ClassifierMixin):
def sigmoid(self, A):
return 1 / (1 + np.exp(-A))
def fit(self, X, y):
Xb = np.c_[np.ones((len(X), 1)), X] # バイアス項の追加
m, n = Xb.shape
theta = np.random.rand(n, 1) # ランダムに初期化
for _ in range(1000):
grad = np.matmul(Xb.T, self.sigmoid(Xb.dot(theta)) - y.reshape(-1, 1))
theta -= 0.01* grad
self.theta = theta
return self
def predict(self, X):
Xb = np.c_[np.ones((len(X), 1)), X] # バイアス項の追加
pred = self.sigmoid(Xb.dot(self.theta)) >= 0.5
return pred
学習率は適当に0.01としました。irisの分類ではよい精度が出ています。
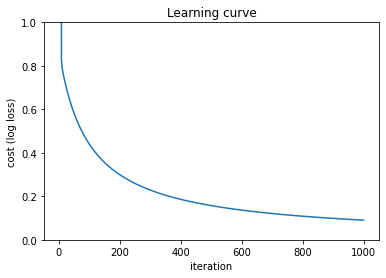
ここでは1000イテレーション繰り返しました。イテレーションを追うごとにパラメータの精度がどう変化しているのかグラフにしてみると以下のようになります。データはirisのクラス0と1を使用しました。
最初の方は値があまりにも大きかったので省きましたが、最大で800くらいありました。しかし10イテレーション足らずでコスト関数の値は1以下まで下がったのち、徐々に精度を上げていって、1000イテレーション後には0.1ほどまで下がりました。
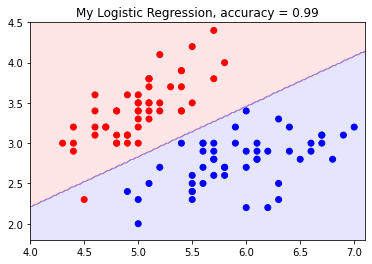
また、irisの特徴量0と1のみを使った場合の結果を可視化すると以下のようになります。
かなりよさげな直線が引けていますね。99%の分類精度を出すことができました。ちなみに「ロジスティック回帰とは何か?」の節で示した図はsklearn.linear_model.LogisticRegressionを用いたものですが、こちらは100%の分類精度を出しています(学習データをそのままテストに使ったので信頼できる数字ではないのですが)。実はsklearnのロジスティック回帰はデフォルトで最急降下法ではなくLBFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm)というアルゴリズムを使っています。僕は詳細は分かりませんが、最急降下法のように勾配を使って徐々にパラメータを改善していくというプロセスは同じなようです。
まとめ
お疲れさまでした!個人的には線形回帰との共通点がさまざまなところで見いだせたのが面白かったです。
ロジスティック回帰の説明は以上になります。誤植や間違いなどありましたら教えていただけると嬉しいです。最後まで読んでいただきありがとうございました!