機械学習を数学を用いないで説明することが人気ですが、逆に機械学習を数学的に理解してみようと思ったことはありませんか?
この記事では機械学習の最も基本的なアルゴリズムの一つである線形回帰(Linear Regression)モデルの仕組みを数式を用いて説明します。
前提知識
- 機械学習の基礎知識
- 用語とかプロセスとか
- 学部1年程度の線形代数と解析学
- 線形代数の方は行列の積と転置を使います
- 解析学の方は偏微分や勾配を使います
参考資料
- Aurelien Geron "Hands-on Machine Learning with Scikit-Learn & Tensorflow"
- モデルの原理の説明や数式の一部を参考にしました。
線形回帰とは何か?
線形回帰では、独立変数$x_1, x_2, x_3, \dots, x_n$から従属変数$y$の値を予測します。独立変数は特徴量、従属変数はターゲット変数と呼んだりもします。線形という名の通り、$y$の値は特徴量の1次関数で予測されます。
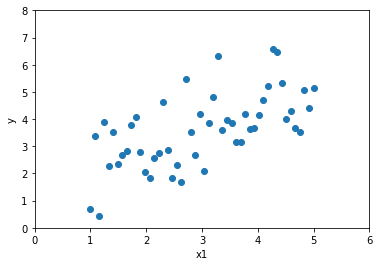
具体的にどうなるのか見ていきましょう。まずは特徴量が1つの場合を考えます。以下のようなデータが与えられたとします。
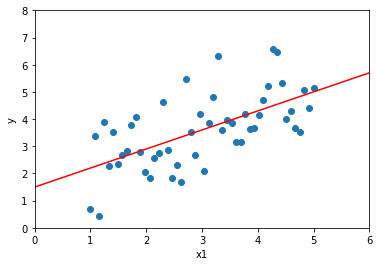
このデータを直線で近似すると以下のようになります。
この直線はデータをもっともよく表現している直線で、回帰直線と呼ばれます。この回帰直線を求めることで、$y$がわからないデータが与えられても、$x_1$の値から大体の$y$の値を予測することができるのです。
ところで、直線の式は以下のように表されます。
y = \theta_0 + \theta_1 x_1
$\theta_0$や$\theta_1$の値はパラメータと呼ばれます。データをもっともよく近似できるようなパラメータの値を探すことが、線形回帰の目的です。
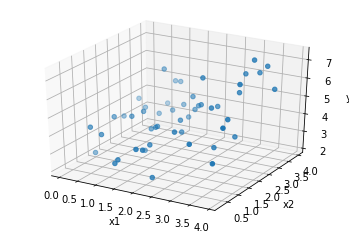
特徴量を1つ増やしてみてみましょう。つまり、今度は$x_1$と$x_2$から$y$の値を予測します。以下のようなデータが与えられたとしましょう。
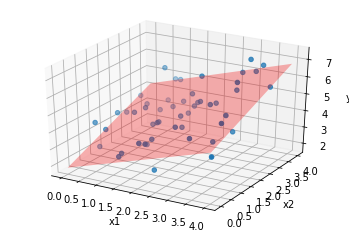
これを$x_1$と$x_2$の一次関数で近似したいです。つまり、$y$を以下のような式で近似したいわけです。
y = \theta_0 + \theta_1 x_1 + \theta_2 x_2
この式は今度は直線ではなく、平面を表しています。与えられたデータを平面で近似することになります。実際には以下のようになります。
$n \geq 3$のときは視覚化することは難しいですが、以上と同様のことができます。
ベクトルを用いた定式化
今まで述べたことを一般化してみましょう。$n$個の特徴量$x_1, x_2, x_3, \dots, x_n$が与えられたとき、$y$の予測値$\hat{y}$は以下のように表されます。
\hat{y} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + a_n x_n
ここでは、真の値を$y$、予測値を$\hat{y}$で表すことにします。ここで、上の式はベクトルを用いると次のように表されます。
\hat{y} = \begin{pmatrix}
\theta_0 & \theta_1 & \theta_2 & \dots & \theta_n
\end{pmatrix}
\begin{pmatrix}
1 \\
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
左のベクトルは個々のパラメータを集めたものです。これらを全部まとめてパラメータと呼ぶことにします。パラメータは列ベクトル$\boldsymbol{\theta}$で表されます。
一方右のベクトルは特徴量を集めたものです。しかし1番上に1というのが入ってますね。これはもともとの特徴量には入っていませんが、0番目の特徴量として便宜的に追加したもので、バイアス項と呼ばれます。これは1次関数の切片に相当します。バイアス項がないと、予測モデルは必ず原点を通ってしまうため、正確なモデルが作れないことがあります。これも、バイアス項と個々の特徴量を全部まとめて特徴量と呼ぶことにします。特徴量は列ベクトル$\boldsymbol{x}$で表されます。
これらの記法を使うと、$\hat{y}$はこのように表されます。
\hat{y} = \boldsymbol{\theta}^T \boldsymbol{x}
$\boldsymbol{\theta}^T$は$\boldsymbol{\theta}$の転置を表します。ベクトルの内積を行列の積として表すために、列ベクトルである$\boldsymbol{\theta}$を行ベクトルに変形しています。
予測値$\hat{y}$をパラメータ$\boldsymbol{\theta}$と特徴量$\boldsymbol{x}$の積として定式化できました。次にパラメータの決定、つまり学習の手法を説明します。
コスト関数
パラメータ$\boldsymbol{\theta}$が変わると、当然予測の精度も変化します。そこで、パラメータが「どれだけ良いか」を測る指標が欲しいなとなります。
そこで、コスト関数というものを考えます。これは予測が真の値からどれだけ離れているかを表す関数で、コスト関数の値が大きいほどパラメータが悪く、小さいほどパラメータが良いことになります。そしてコスト関数の値ができるだけ小さくなるようなパラメータを探していけばよいことになります。
コスト関数は予測値$\hat{y}$と真の値$y$の離れ具合を測れればいいのでいろいろなものが考えられますが、主に使われているのは誤差の2乗和です。すべての学習データについて、パラメータを用いた予測値と真の値の誤差の2乗を計算し、その和を取ったものをコスト関数とするのです。
なぜ絶対値ではなく2乗なのかと疑問に思うかもしれませんが、そうするとコスト関数の導関数が連続になってうれしいのです。コスト関数の導関数にはもう少し後で触れます。
このように、誤差の2乗の和を用いてパラメータを決定する手法を最小二乗法と呼びます。これは1800年代初期にすでに発案されていたというのですから驚きですね。
それでは数式を用いてコスト関数を表していきます。コスト関数を$J(\boldsymbol{\theta})$とすると、
\begin{align}
J(\theta) &= \sum_{i=1}^{m} \left( \hat{y}^{(i)} - y^{(i)} \right)^2 \\
&= \sum_{i=1}^{m} \left( \boldsymbol{\theta}^T \boldsymbol{x}^{(i)} - y^{(i)} \right)^2
\end{align}
新しい文字や記法が出てきたので1つ1つ説明していきます。まず$m$は与えられたデータの数を表しています。なので$\sum$はデータすべてに対して誤差の2乗の和を取るということを表しています。次に$\boldsymbol{x}$や$y$の右肩にある$(i)$は、「$i$番目のデータの」ということを表しています。つまり$\boldsymbol{x}^{(i)}$は$i$番目のデータの特徴量を表しているということになります。
パラメータの決定
コスト関数の偏微分を求める
コスト関数が定義できたところで、これを最小にするようなパラメータ$\boldsymbol{\theta}$の値が知りたいです。関数の最小値を求めるには、微分をします。
コスト関数$J$の変数はベクトル$\boldsymbol{\theta}$なので、ベクトルの要素$\theta_0, \theta_1, \theta_2, \dots, \theta_n$を変数とした多変数関数とみることができます。よってこれらの変数それぞれを使って偏微分をしていくことになります。$J(\boldsymbol{\theta})$を$j$番目の特徴量の係数$\theta_j$で偏微分していきましょう。
\begin{align}
\frac{\partial}{\partial \theta_j} J(\boldsymbol{\theta}) &= 2 \sum_{i=1}^m \left( \boldsymbol{\theta} ^ T \boldsymbol{x}^{(i)} - y^{(i)} \right) x^{(i)}_j \\
&= 2 \sum_{i=1}^m \left( \hat{y}^{(i)} - y^{(i)} \right) x^{(i)}_j
\end{align}
ここでは合成関数の微分を使いました。$\theta_j$の係数は$x^{(i)}_j$ ($i$番目のデータの$j$番目の特徴量)なので、それが括弧の外に出ます。
実はこの式は新しい文字を導入するとさらに簡単にできます。入力の特徴量全体を$m \times (n+1)$行列$X$で表します。$X$の$i$行目は$i$番目のデータの特徴量を表すベクトルです。つまり$X$の$i$行目は$\left( \boldsymbol{x}^{(i)} \right)^T$となります。$X$の$j$列目は$j$番目の特徴量を表しています。ここで$j$は0から始まることに注意してください。以上のことをまとめると、
X_{ij} = x^{(i)}_j
ということになります。
ではここで、$X\boldsymbol{\theta}$とは何を表しているでしょうか?列ごとに分解して考えると、
X \boldsymbol{\theta} = \begin{pmatrix}
\left( \boldsymbol{x}^{(1)} \right)^T \\
\left( \boldsymbol{x}^{(2)} \right)^T \\
\vdots \\
\left( \boldsymbol{x}^{(m)} \right)^T
\end{pmatrix} \boldsymbol{\theta}
= \begin{pmatrix}
\left( \boldsymbol{x}^{(1)} \right)^T \boldsymbol{\theta} \\
\left( \boldsymbol{x}^{(2)} \right)^T \boldsymbol{\theta} \\
\vdots \\
\left( \boldsymbol{x}^{(m)} \right)^T \boldsymbol{\theta}
\end{pmatrix}
= \begin{pmatrix}
\left( \boldsymbol{\theta}^T \boldsymbol{x}^{(1)} \right)^T \\
\left( \boldsymbol{\theta}^T \boldsymbol{x}^{(2)} \right)^T \\
\vdots \\
\left( \boldsymbol{\theta}^T \boldsymbol{x}^{(m)} \right)^T
\end{pmatrix}
$\boldsymbol{\theta}^T \boldsymbol{x}^{(i)}$はスカラーなので、転置は無視できます。結局、
X \boldsymbol{\theta} = \begin{pmatrix}
\boldsymbol{\theta}^T \boldsymbol{x}^{(1)} \\
\boldsymbol{\theta}^T \boldsymbol{x}^{(2)} \\
\vdots \\
\boldsymbol{\theta}^T \boldsymbol{x}^{(m)}
\end{pmatrix}
= \begin{pmatrix}
\hat{y}^{(1)} \\
\hat{y}^{(2)} \\
\vdots \\
\hat{y}^{(m)}
\end{pmatrix}
ということになります。ここで$\boldsymbol{y}$をデータの真の値を表す列ベクトル
\boldsymbol{y} = \begin{pmatrix}
y^{(1)} \\
y^{(2)} \\
\vdots \\
y^{(m)}
\end{pmatrix}
と定義します。また、$\boldsymbol{x}_j$を$X$の$j$列目とします。これはすべてのデータの$j$番目の特徴量を集めたものになります。すると、コスト関数は
\begin{align}
\frac{\partial}{\partial \theta_j} J(\boldsymbol{\theta}) &= 2 \sum_{i=1}^m \left( \hat{y}^{(i)} - y^{(i)} \right) x^{(i)}_j \\
&= 2\boldsymbol{x}_j^T (X\boldsymbol{\theta} - \boldsymbol{y})
\end{align}
で表されます。
勾配を求める
偏微分ができたところで、勾配ベクトルを求めます。$n$変数スカラー関数$f$の勾配$\nabla f$とは
\nabla f = \begin{pmatrix}
\frac{\partial f}{\partial x_1} \\
\frac{\partial f}{\partial x_2} \\
\vdots \\
\frac{\partial f}{\partial x_n}
\end{pmatrix}
のことでした。$J(\boldsymbol{\theta})$の勾配は
\begin{align}
\nabla J(\boldsymbol{\theta}) &= \begin{pmatrix}
2\boldsymbol{x}_0^T (X\boldsymbol{\theta} - \boldsymbol{y}) \\
2\boldsymbol{x}_1^T (X\boldsymbol{\theta} - \boldsymbol{y}) \\
\vdots \\
2\boldsymbol{x}_n^T (X\boldsymbol{\theta} - \boldsymbol{y})
\end{pmatrix} \\
&= 2 \begin{pmatrix}
\boldsymbol{x}_0^T \\
\boldsymbol{x}_1^T \\
\vdots \\
\boldsymbol{x}_n^T
\end{pmatrix} (X\boldsymbol{\theta} - \boldsymbol{y}) \\
&= 2 \begin{pmatrix}
\boldsymbol{x}_0 & \boldsymbol{x}_1 & \dots & \boldsymbol{x}_n
\end{pmatrix}^T (X\boldsymbol{\theta} - \boldsymbol{y}) \\
&= 2X^T (X\boldsymbol{\theta} - \boldsymbol{y})
\end{align}
だいぶきれいな式が得られました。
パラメータの決定と実装例
それではこの勾配の式を使ってコスト関数$J(\boldsymbol{\theta})$が最小となるパラメータ$\boldsymbol{\theta}$を求めていきます。このコスト関数は連続なので、勾配が$\boldsymbol{0}$になるところで極小値または極大値を取ります。しかし$J(\boldsymbol{\theta})$の値はいくらでも大きくできることが直感的にわかるので、勾配が$\boldsymbol{0}$になるところは極小値になります。
\begin{align}
2 X^T (X \boldsymbol{\theta} - \boldsymbol{y}) &= \boldsymbol{0} \\
(X^T X) \boldsymbol{\theta} &= X^T \boldsymbol{y} \\
\therefore \boldsymbol{\theta} &= (X^T X)^{-1} X^T \boldsymbol{y}
\end{align}
これでパラメータ$\boldsymbol{\theta}$を決定することができました!以下にPythonでの実装例を示します。(sklearnはなくてもいいですがあった方がいいと思います)
import numpy as np
from sklearn.base import BaseEstimator, RegressorMixin
class MyLinearRegression(BaseEstimator, RegressorMixin):
def fit(self, X, y):
Xb = np.c_[np.ones((len(X), 1)), X] # バイアス項の追加
self.theta = np.linalg.inv(Xb.T.dot(Xb)).dot(Xb.T).dot(y.reshape(-1, 1))
return self
def predict(self, X):
Xb = np.c_[np.ones((len(X), 1)), X] # バイアス項の追加
pred = Xb.dot(self.theta)
return pred
まとめ
お疲れさまでした!ここまで式を追うのは大変だったかもしれませんが、自分で手を動かして計算しながら式を追っていくとよいと思います。
途中で変数がたくさん出てきたので少し混乱しているかもしれません。ここで、途中式や変数の細かい定義を省いて結果だけもう一度まとめます。
$n$個の特徴量を持つ$m$個のデータが与えられます。データを$m \times (n+1)$行列$X$で表します。$X_{ij}$は$i$番目のデータの$j$番目の特徴量を表します。また独立変数の
$X$の$i$行目($i = 1, 2, \dots, m$)は$i$番目のデータを表しており、$j$列目($j = 0, 1, \dots ,n$)は$j$番目の特徴量を表します。また、ターゲット変数の真の値$y$を列ベクトル$\boldsymbol{y}$で表します。$\boldsymbol{y}$の$i$行目は$i$番目のデータのターゲット変数の真の値です。ここで列ベクトル$\boldsymbol{\theta}$ (パラメータ)を使って、$X\boldsymbol{\theta}$の$i$行目を$i$番目のデータに対する予測値$\hat{y}$とします。予測値と真の値の2乗和が最小になるようなパラメータ$\boldsymbol{\theta}$は、
\boldsymbol{\theta} = (X^T X)^{-1} X^T \boldsymbol{y}
で与えられます。
線形回帰の説明は以上になります。誤植や間違いなどありましたら教えていただけると嬉しいです。最後まで読んでいただきありがとうございました!