RAMEN-SHIO-235B - 事後学習の軌跡

はじめに

本記事では、東京大学松尾・岩澤研究室主催のLLM開発コンペ2025における、チームRAMEN決勝での事後学習の取り組みについてまとめます。
チームRAMEN決勝では、Qwen/Qwen3-235B-A22B-Thinking-2507の追加学習によって RAMEN-SHIO-235B を開発し、Humanity's Last Exam (HLE) においてオープンソースモデルでトップレベルの性能を達成して優勝しました。
3週間という限られた期間での開発の過程を記録として残したいと思います。

※具体的な実装例については載せていないので、チームRAMENの別記事をご参考ください。

プロジェクト概要

まず、コンペのルールなど前提についてまとめます。

コンペティションの背景

本コンペは予選と決勝フェーズで開催されました。予選の結果、12チーム中上位3チームが決勝に進出し、チームRAMENは3位で決勝進出を果たしました。（筆者は予選は別チームで敗退しましたが、決勝からRAMENに参加させていただきました）

コンペの評価は、 Humanity's Last Exam (HLE) という高難易度のベンチマークと、安全性ベンチマークであるDo-Not-Answer（DNA）で行われます。HLEは博士課程レベル、あるいはそれ以上の専門知識と推論力が求められる問題で構成され、既存のLLMでも高スコアを出すことが困難なベンチマークです。
本コンペではDNAよりもHLEの方が配点が高いため、HLEにおいて最高性能（SOTA）を達成することを目標とし、開発に取り組みました。

今回は既存のLLMを追加学習して性能を引き上げる形式のため、ベースモデル選定も重要でした。ベースモデルは指定されたリストから選択しますが、モデルの特性やライブラリとの相性、計算資源・期間の制約を踏まえて、限られた時間内に性能を改善できる戦略が必要です。

また、本コンペは推論モデル (reasoning model) の開発が前提となっています。推論モデルはOpenAI o1やDeepSeek-r1のように、推論トークンを用いて内部で段階的に思考してから回答を生成するのが特徴です。推論過程の扱いは実装によりますが、<think>タグ内で推論し、その後最終的な回答を出力するモデルが多いです。

チームRAMENでは、予選で235BモデルでのSFTに成功していたため、決勝ではその経験を活かしつつ、強化学習などより高度な学習手法を取り入れることで、さらなる性能向上を目指しました。

制約条件

期間
決勝に与えられた期間は3週間です。この限られた時間の中で、データ準備、学習、評価を完了させる必要があり、かなりタイトなスケジュールでした。

計算リソース
各チームH100 × 64枚（8ノード）が利用可能でしたが、データ生成や評価にもGPUを使う必要があったため、235Bモデルの学習に使えるリソース程度は実質4ノード（32枚）程度でした。

学習コード
予選時に、コンペ運営から動作確認済みの学習コードが提供されており、verlを使用したSFTは実行可能な状態でした。verlはLLM向けの強化学習ライブラリで、最近注目されているGRPOにも対応しています。予選での経験から、シングルノードでのGRPOは経験のあるメンバーが複数名いました。

初期戦略

決勝開始当初の戦略は以下のとおりです。

ベースモデル選定

チームRAMENでは、ベースモデルとして Qwen/Qwen3-235B-A22B-Thinking-2507 を採用しました。
選定理由

• HLEを含む複数ベンチマークにおいて、オープンモデルの中でトップクラスの性能
• 予選で同系列モデル（Qwen/Qwen3-235B-A22B-Instruct-2507）のSFT実績があり、SFTに関しては学習可能な状態

一方で、本モデルはMoE構造を採用しているため、利用する学習フレームワークや並列化方式との相性に注意が必要であり、ライブラリ側の対応状況も踏まえて開発を進めていく必要がありました。

学習方針

決勝開始時の学習戦略はSFTとGRPOという２つの手法を検討する方針でした。

戦略1: SFT（Supervised Fine-Tuning）
SFT は、教師データ（入力 $x$ と望ましい出力 $y^*$）を用いてモデルを微調整する手法です。与えられた入力 $x$ に対し、望ましい出力 $y^*$ を得られるように、次の損失関数を最小化します。

\mathcal{L}_{\mathrm{SFT}}(\theta)
= \mathbb{E}_{(x, y^\star)\sim\mathcal{D}}
\left[ - \log \pi_\theta(y^\star \mid x) \right]

ここで、$\theta$ はモデルのパラメータ、$\mathcal{D}$ は教師データセットを表します。モデルは、$\pi_\theta(y^\star \mid x)$（入力$x$が与えられたときに正解$y^*$を出力する条件付き確率）を最大化するようにパラメータを更新していきます。

今回は、保守的な戦略としてSFTを検討しました。SFTのメリットは、実装が容易で、比較的 短時間で学習可能な点です。一方で、改善幅が限定的であり、過学習を招くリスクも指摘されています（詳細は Appendix 参照）。性能面では懸念があるものの、235BモデルのSFTは予選で実績があり、学習コードもすでに整備されていたため、限られた期間で確実に提出可能なモデルを構築できる堅実な選択肢となりました。

戦略2: GRPO（Group Relative Policy Optimization）
GRPOは、オンライン強化学習の手法で、1 つの質問（プロンプト）に対して複数の応答を生成し、そのグループ内での相対的な優劣をもとにポリシー（モデル）を更新していきます。

GRPO の目的関数は次のように記述されます。

J_{\mathrm{GRPO}}(\theta)=\mathbb{E}\!\left[q\sim P(Q),\,\{o_i\}_{i=1}^{G}\sim\pi_{\theta_{\mathrm{old}}}(O\mid q)\right]\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_i|}\sum_{t=1}^{|o_i|}\left\{\min\!\left(\frac{\pi_\theta(o_{i,t}\mid q,o_{i,<t})}{\pi_{\theta_{\mathrm{old}}}(o_{i,t}\mid q,o_{i,<t})}\hat{A}_{i,t},\,\mathrm{clip}\!\left(\frac{\pi_\theta(o_{i,t}\mid q,o_{i,<t})}{\pi_{\theta_{\mathrm{old}}}(o_{i,t}\mid q,o_{i,<t})},1-\varepsilon,1+\varepsilon\right)\hat{A}_{i,t}\right)-\beta D_{\mathrm{KL}}\!\left[\pi_\theta\|\pi_{\mathrm{ref}}\right]\right\}

ここで、$\{o_i\}_{i=1}^{G}$ は 1 つの質問に対して生成された $G$ 個の応答、$\hat{A}_{i,t}$ はそれぞれのトークンに対する相対的なアドバンテージ、$\pi_{\theta_{\mathrm{old}}}$ は更新前のポリシー、KL 項は参照ポリシーからの乖離を抑制するためのペナルティです。複数の応答の中で相対的に優れているものを強化することで、絶対値のスコアに依存しすぎない安定した学習が可能になります。

DeepSeek-R1をはじめ、既存モデルでGRPOが性能向上に寄与している結果を踏まえ、特に難問に対する推論能力の向上を期待してGRPOを検討しました。また、報酬モデルをLLMではなくルールベースで設計（RLVR）することで、計算コストを抑えられる点も重要でした。例えば、数学タスクであれば「最終的な解が正しいか」、選択問題であれば「正答選択肢を選べているか」といった単純な判定ルールで報酬を定義でき、報酬モデル用の計算リソースを割かずに強化学習できます。

GRPOはSFTと比較して過学習しづらく、汎化性能の向上が期待される一方、実装の複雑さ、学習の不安定性がリスクとしてありました。

課題

決勝開始時点では、以下の課題が懸念されました。

ベースモデルが強すぎる問題
強力なベースモデルでは、追加学習をすることで性能が低下するケースが予選で多く確認されていました。すでに事後学習が完了している最適化されたモデルに対して追加学習を行うと、既存のバランスを崩してしまい、調整が難しくなります。今回選択したベースモデルはオープンモデルでトップレベルの性能であり、更に性能を上げるためには、データや学習条件を慎重に調整する必要がありました。

マルチノードGRPOの未経験
235Bモデルの学習にはマルチノード学習が必要ですが、GRPOをマルチノード環境で動かした経験が無く、実装面で懸念がありました。SFTと異なり、GRPOでは推論と学習（パラメータ更新）を繰り返し行うため、メモリ管理が複雑になります。さらに、シングルノードでの試行結果から、学習に相当な時間がかかることが分かっており、3週間という期間内に十分なPDCAサイクルを回せるかが不透明でした。

序盤: SFTの試行とGRPO実装の壁

プロジェクト序盤では、SFTとGRPOの二つの軸で検証を進めました。

SFTの試行

運営提供コード（verl）による試行
SFTは、運営から提供された verl のサンプルコードで、LoRAの学習を開始しました。しかし、235Bモデルでは、1万サンプルの学習に約20時間かかり、このままでは限られた期間内で十分な試行錯誤を行うことが困難であることが判明しました。

ms-swift (Megatron) への移行
学習速度のボトルネックを解消するため、ms-swift（Megatron） への移行を行いました。

Megatronバックエンドを採用したことで、学習を高速化できました。MegatronではEP（Expert Parallelism）などMoEモデル向けの並列化手法を活用でき、verlのFSDP（Fully Sharded Data Parallel）と比べて学習速度が10倍程度向上しました。この高速化により、限られた時間でより多くの実験を回せる見通しが立ちました。

さらに、Singularityコンテナを使うことで、環境構築が容易になりました。verlでは環境をcondaで一から構築していましたが、ms-swiftのdockerイメージをSingularity形式に変換して使用することで、チームメンバーが同じ環境で安定して学習を実行できるようになりました。（今回の環境では、権限の関係でdockerを使用できませんでしたが、Singularityは使用可能でした。）

また、性能向上の可能性を探るため、ms-swiftでサポートされていた DFT（Dynamic Fine-Tuning） も検討対象としました（詳細はAppendix参照）。

性能退化の課題
しかし、SFTの実験では、学習前と比べてHLEスコアが低下する傾向が見られました。これは、ベースモデルと学習データの分布の差異による分布シフトが主な要因と考えられます。

この問題を緩和するため、学習率の調整や、LoRAの派生手法（OLoRAやrsLoRA）の適用など、複数の設定を試行しましたが、いずれの場合もベースモデルの性能を超えることはできませんでした。

GRPOの実装

SFTと並行して、マルチノードGRPOの実装にも着手しました。ライブラリはms-swiftとverlを検討し、それぞれ環境構築と検証を進めました。

ms-swiftによるGRPO

ms-swiftでのGRPOでは、分散学習にDeepSpeed、推論サーバとしてvLLMを使用可能です（現時点では、MegatronでのGRPOは未対応）。

検証の結果、シングルノードでのGRPOは成功しましたが、マルチノードではvLLMでの推論処理が上手く行かず、ms-swiftでのGRPOは断念しました。（詳細はこちらの記事参照）

verlによるGRPO

verlでは、FSDPとMegatronの２種類のバックエンドを選択できます。Qwen3-235B-A22B向けの公式サンプルコードではMegatronが用いられており、MoEモデルに適した並列化が実装されていることから、本プロジェクトでもMegatronが有力候補と考えられました。一方で、運営提供コードの環境ではFSDPが利用可能で、Megatronを使うには環境構築からやり直す必要があったため、リスク分散の観点からFSDPとMegatronを並行して検証することにしました。

各バックエンドの課題
FSDPでは、235Bモデルで GRPO を実行できることは確認できたものの、MoE向けに最適化されていないこともあり、メモリ使用が不安定で、学習中にOOM（Out of Memory）エラーが発生することがありました。

Megatronでは、環境構築から着手しましたが、ライブラリの依存関係が複雑で、安定した実行環境の構築に時間がかかりました。公式の設定を参考にすることで、動作可能な環境は構築できたものの、チーム内で再現可能な形には至らず、残り時間を考えると難しい状況になりました。（今思えば、Singuralityコンテナを使用したら、環境の再現性問題は解決できたかもしれません）

学習時間長すぎ問題
シングルノードでの試行から、推論部分がGRPOに要する時間の大半を占めることが分かっており、SFTと比較すると1回のGRPO実験に時間が長くかかりました。そのため、残り2週間で十分な試行回数を確保し、PDCAサイクルを回すのが難しい状況でした。推論エンジンをvLLM→SGLangに切り替えることで推論処理の高速化にも取り組みました（参考）が、それでもSFTと比べると数十倍以上の時間がかかっていました。

中盤: 戦略転換

プロジェクト2週目に入り、当初の戦略を大きく変更することになりました。

GRPOの断念

序盤の試行で、GRPOでは以下の問題を抱えていました。

• マルチノード環境での不安定性（通信エラー、OOM）
• 環境構築の再現が取れていない（学習を回せる人が少ない）
• 1回の学習に数日以上かかり、実験サイクルを回しづらい

この状況を受けて、GRPOの断念を決断しました。

しかしながら、SFTでは性能向上が難しい状況でもあったため、学習コストが低く、性能向上を見込める手法を検討する必要がありました。

オンライン強化学習 vs オフライン強化学習

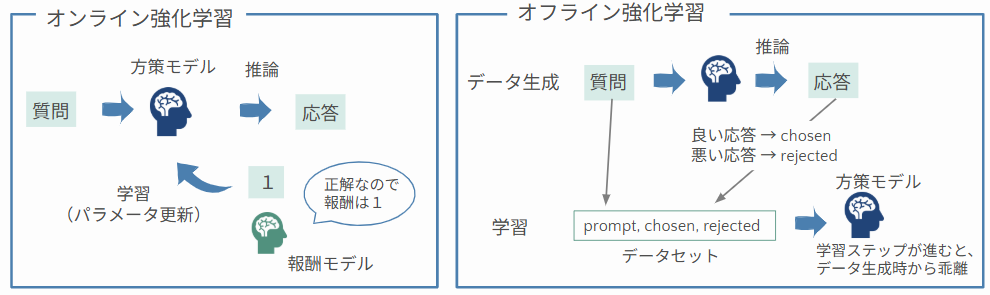
戦略変更にともない、チーム内で活発な議論が行われました。中心となったのは、オンライン強化学習とオフライン強化学習、どちらに注力すべきかということです。LLM の強化学習では通常、方策モデルが生成した応答に対してフィードバック（報酬）を与えてモデルを更新していきます。手法としては大きくオンライン型とオフライン型に分けることができます。

オンライン強化学習の特徴

• 学習ステップごとに、推論（データ生成）と学習（パラメータ更新）を繰り返す
• 最新のモデルの振る舞いに基づいて改善できる
• 計算コストが高く、実装が複雑になりやすい
• 代表的な手法：PPO, GRPO, GSPO

オフライン強化学習の特徴

• 事前に用意したデータセット（例：(prompt, chosen, rejected)のペア）用いてモデルを学習する
• データは「学習前モデルのポリシー」に依存しており、学習が進むにつれてモデルの分布と乖離する
• 学習中に新たなサンプルを生成する必要がないため、実装がシンプルで学習が高速
• 代表的な手法：DPO, KTO, ORPO

今回の場合は、残り約2週間で十分な試行回数を確保するためにオンライン手法は見送り、オフライン強化学習に軸足を移す判断をしました。中でも、既に多くの事例で有効性が示されている DPO（Direct Preference Optimization） に取り組むことになりました。

DPOでは、(prompt, chosen, rejected)のペアに対して、方策$\pi_\theta$がchosen（$y_w$）をrejected（$y_l$）より好むように最適化します。損失関数は以下のとおりです。

\mathcal{L}_{\mathrm{DPO}}(\pi_\theta;\pi_{\mathrm{ref}})
= -\,\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}
\Big[
  \log \sigma\!\Big(
    \beta \log \frac{\pi_\theta(y_w\mid x)}{\pi_{\mathrm{ref}}(y_w\mid x)}
  - \beta \log \frac{\pi_\theta(y_l\mid x)}{\pi_{\mathrm{ref}}(y_l\mid x)}
  \Big)
\Big]

最近では、rejectedの設計が学習結果に強く影響することが指摘されています。特に、生成確率は高いが実際には不適切な応答（モデルが“自信を持って間違える”ケース）をrejectedに選ぶことが有効、という報告があります（Cho et al., 2025）。

新たな方針

戦略転換後は、SFTとオフライン強化学習を主軸とする方針になりました。

• SFT・DFT（ms-swift Megatron）を継続
• オフライン強化学習としてDPOを導入
  • DPOはms-swift（Megatron）でサポートされており、高速な学習が可能
• Opt-Deusによる層拡張も検討
• いきなり235Bモデルで試すのはコストが高いため、30Bモデル（Qwen/Qwen3-30B-A3B-Thinking-2507）で各手法を比較検証
  • 対象の手法: SFT、DFT、DPO
  • 各手法を「30Bモデル」と「Opt-Deusで30Bを層拡張したモデル」それぞれについて検証

30Bでの検証結果を踏まえて、最も有望な手法を235Bに適用することになりました。

30Bモデルでの検証

30Bモデル（Qwen/Qwen3-30B-A3B-Thinking-2507）を用いて、複数手法を実験しました。

実験結果の傾向

30BモデルとOptdeusを適用して層拡張した30Bモデルに対して、各事後学習手法を適用後のHLEスコアを図1に示します（同一手法内でも、データセットや学習パラメータは試行ごとに異なります）。

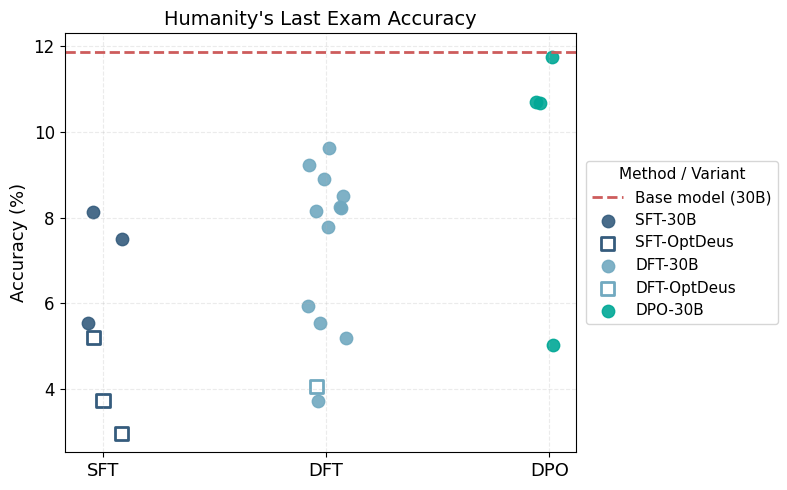
図1. 30Bモデルでの各手法におけるHLE正答率の比較

SFTやDFTでは多くの設定で、ベースモデルの11.9%から大きく性能が低下しました。
一方、DPOは概ねベースモデルと同程度の性能を維持しており、大きな劣化は見られませんでした（Accuracyが5%付近の点については、後の調査でデータ不備が原因であったことが判明しています）。
さらに、この段階ではDPOのハイパーパラメータ（学習率や$\beta$など）を十分に探索できておらず、調整により改善余地があると見込まれました。

以上を踏まえ、終盤はDPOに集中する方針が固まりました。
ただし、30Bの実験では、いずれの手法もベースモデルを明確に上回る改善には至らず、DPOでも「ほぼ同程度」の水準に留まりました。そのため、ベースモデル超えを実現するためにはデータ品質の改善が重要と判断し、データ班でのデータ改善を行ったうえで、235Bモデルでの学習へと進むことになりました。

終盤: 235BモデルでのDPO

プロジェクト終盤は、30Bモデルでの知見を基に、235BモデルでのDPOに集中しました。

DPOの実装

DPOは ms-swift (Megatron) で実装しました。

学習データは、ベースモデルである Qwen3-235B-A22B-Thinking-2507 自身に問題を解かせ、その出力から構成しました。

具体的には、

• モデルのTemperatureを高めに設定し、同じ問題に対して複数回答を生成
• 正解の出力を chosen、不正解の出力を rejected としてペアを作成

という流れです（参考）。

これまでの検証から、モデルが生成するデータ分布と大きく異なるデータで学習すると性能劣化しやすいことが分かっていたため、モデル自身の分布に沿った応答を用いることで、分布シフトを抑えながら好ましい振る舞いを強化することを狙いました。
オンライン強化学習であるGRPOが「同じ質問に対する複数応答の相対評価」をオンラインで行うのに対し、今回のDPOはその狙いをオフラインで近似的に実現していると考えられます。

データ班で用意した複数パターンのデータセットを検証しつつ、DPOのハイパーパラメータ探索を進めました。

ハイパーパラメータ探索

コンペ終了まで残り２日となり、 LoRA 設定・学習率・β・学習対象層・データ構成 を変えながら、最適な組み合わせを探っていきました。

調整したパラメータ

• LoRA rank / alpha：LoRAで追加する低ランク行列の容量を決めるパラメータ。大きくするとタスクへの追従性と表現力は上がる一方、元モデルの分布を崩しやすく、過学習や性能劣化のリスクも高まる。小さくすると挙動は安定しやすいが、更新の自由度が不足し、改善幅は限定的になる。alphaはrankの2倍程度に設定するケースが多い。
• lr（学習率）：パラメータ更新のステップ幅を決める値。大きくすると収束は速くなるが不安定になりやすく、小さすぎると安定する代わりに収束が遅くなる場合がある。
• beta ($\beta$)：学習前のモデルからどれだけ逸脱できるか（KL制約の強さ）と、chosen / rejected の好み差のスケールを決める係数。大きくするとKLペナルティが強くなり、参照モデルに近い保守的な更新になる。小さくするとKLペナルティが弱まり、参照モデルから逸脱しやすくなる。
• target_module：LoRA を適用する層の指定。線形層や MoE routerなどを設定可能。

試行した主な設定とHLEスコアは以下のとおりです。

表1. DPOパラメータとHLEスコア

id	HLE_score	dataset	rank	alpha	lr	beta	target_module
#59	17.89	DS1	16	32	5e-5	0.1	all-linear
#64	19.12	DS2	16	32	5e-5	0.1	all-linear
#65	17.16	DS1	16	32	5e-5	0.1	all-linear, all-router
#66	16.79	DS1	64	128	5e-5	0.1	all-linear
#67	18.62	DS3	16	32	5e-5	0.1	all-linear
#68	17.28	DS3	16	32	1e-6	0.01	all-linear
#69	17.52	DS2	16	32	1e-6	0.01	all-linear
#70	19.12	DS3	16	32	2e-5	0.075	all-linear

最終的に、#70 の設定で最も高いHLEスコアを達成したため、これが提出モデル（RAMEN-SHIO-235B）となりました。（#64と#70はここでは同スコアですが、他データでの評価結果等を踏まえて#70に決定しました）

以下に、主な検証ポイントをまとめます。

データセットによる違い

データ作成と学習を同時並行で進めていたため、複数のデータセット（DS1, DS2, DS3）を用いてDPOを検証しました。
#59, #64, #67 はLoRAや学習率などの設定を揃え、データセットのみを変更した比較実験になっています。スコアを見ると、単一ソース中心のDS1に比べて、複数ソースを適切な比率で組み合わせた DS2 / DS3 の方がスコアが高く、データ構成の調整が性能向上に直結していることが確認できます。

MoEのrouter部分を学習

ms-swiftによるLoRA学習では、MoEのrouterを学習対象に含めるには all-router を指定する必要があります。routerは各トークンをどのexpertに振り分けるかを決めるgating部分です。#65では all-linearに加えて all-router をtarget_moduleに指定し、all-linearのみを指定した#59と比較して挙動を確認しました。

学習ログより、all-routerを含めた結果、以下の振る舞いを確認しました。

• 学習終盤にlossがより低下
• rewardsのmargins（chosen–rejectedの差）が終盤でより大きい

更新対象パラメータが増えたことで、ログ上は学習がより進んでいるように見えました。
しかしながら、HLE スコアは routerを含めることで約0.7ポイント低下したため、今回はrouterを学習対象に含めない判断をしました。

LoRA rank, alphaの変更

#66では LoRA の rank / alpha を引き上げ、パラメータ容量を増やした構成を検証しました。
#59（rank16, alpha32）と#66（rank64, alpha128）を比較した学習ログを以下に示します。#66ではlossやrewardsが不安定で大きく変動しており、HLEスコアも#59と比較して1.1ポイント低い結果となったため、rankとalphaは控えめの設定とする方針になりました。

時間の都合で検証できませんでしたが、rank / alpha を上げる場合は学習の安定化が必要かもしれません。安定化の手段としては、学習率の引き下げやAdamの$\varepsilon$（eps）の調整などが考えられます。

学習率, βの変更

学習率（lr）と$\beta$は、DPOの効き方を左右する重要なパラメータです。
以下は、学習率と$\beta$以外の条件を揃えて比較した結果です。

id	HLE_score	dataset	rank	alpha	lr	beta	target_module
#67	18.62	DS3	16	32	5e-5	0.1	all-linear
#68	17.28	DS3	16	32	1e-6	0.01	all-linear
#70	19.12	DS3	16	32	2e-5	0.075	all-linear

• #68（lr=1e-6, β=0.01）
  chosenのrewardsがほぼ0付近（rejectedに引っ張られる形でわずかにマイナス）。rejectedのrewardsも浅い下降に留まり、marginsがほとんど伸びない。更新が弱すぎてchosenとrejectedの分離が進まず、学習が鈍化。

• #67（lr=5e-5, β=0.10）
  marginsは大きく、chosen/ rejected の分離ができているが、小さいスパイクが発生しており学習が不安定ぎみ。

• #70（lr=2e-5, β=0.075）
  chosenの上昇・rejectedの下降が安定しており、lossも収束。分離の強さと安定性のバランスが良好。

lrと$\beta$を同時に変えているため厳密な切り分けは難しいものの、学習率の影響が支配的に見えます。#70 はベース分布を崩しすぎずにpreferenceを反映できており、HLEでも高スコア（19.12）を達成したため、提出モデルとして採用しました。学習前のベースモデルのHLEスコア17.77からも向上しており、学習が有効に機能したものと考えられます。

おわりに

3週間という短い期間でしたが、当初想定していた戦略（SFT + GRPO）から状況に応じて方針転換を行い、最終的にはDPOでベースモデルからの性能向上を達成できました。

個人的には、序盤からGRPOに取り組んでいたこともあり、断念せざるを得なくなったときは、正直気持ちが折れかけました。しかし、チームメンバーからの助言もあり、DPOに切り替えた結果、チーム一丸となって最後まで取り組むことができ、最終的に優勝へとつながりました。最後まで諦めずにやり切ることができて、本当に良かったと感じています。

本記事では主要な結果のみを紹介しましたが、実際にはここに書ききれていない試行錯誤や細かな検証が数多くあります。「面白そう」「やってみたい」と感じていただけた方は、ぜひ次の機会に挑戦してみてください。

※2024年のコンペでは、『Tanuki-8B, 8x8B - 事後学習の軌跡』を執筆しました。興味のある方はこちらもご覧ください。

最後に、共に戦い抜いたチームの皆様、このような貴重な機会をご提供いただいた松尾・岩澤研究室の皆様、そしてGPU リソースをご提供くださった さくらインターネット様に心より感謝申し上げます。

本プロジェクトは、国立研究開発法人新エネルギー・産業技術総合開発機構(以下「NEDO」)の「日本語版医療特化型LLMの社会実装に向けた安全性検証・実証」における基盤モデルの開発プロジェクトの一環として行われます。

---

Appendix

ここでは、プロジェクト中に議論・参照した論文のうち、特に SFT の限界とその改善手法（DFT / CHORD） に関するポイントを整理します。

DFT （Dynamic Fine-Tuning）

On the Generalization of SFT: A Reinforcement Learning Perspective with Reward Rectification

この論文では、従来のSFTを 強化学習（RL）の枠組みで定式化し、その一般化性能の限界を理論的に示したうえで、損失関数を修正したDFTを提案しています。

SFT の RL 的な見方

通常の SFT の損失は

\mathcal{L}_{\mathrm{SFT}}(\theta)
= \mathbb{E}_{(x, y^\star)\sim\mathcal{D}}
\left[ - \log \pi_\theta(y^\star \mid x) \right]

と書けますが、これを 疎な報酬 $r(x, y)=\mathbf{1}[y = y^\star]$ と 重要度重み $w(y\mid x)=1/\pi_\theta(y\mid x)$ を用いて書き換えると、

\nabla_\theta \mathcal{L}_{\mathrm{SFT}}(\theta)
= - \mathbb{E}_{x \sim D_x,\, y \sim \pi_\theta(\cdot \mid x)}
\left[ w(y \mid x)\, \nabla_\theta \log \pi_\theta(y \mid x)\, r(x, y) \right]

となり、「確率が低いトークンほど更新が過剰に大きくなる」逆確率バイアスを内包していることが示されます。これが過学習や汎化性能低下の一因になりうる、ということが論文中で指摘されています。

DFT のアイデア

DFT は、この問題を トークン確率に基づく動的な再重み付け によって補正します。直感的には、SFT 勾配に含まれる $1/\pi_\theta$ の要素を打ち消すようにし、極端に低確率なトークンへの過大な更新を抑えます。

論文では、SFT の勾配に対してトークン確率を用いた stop-gradient 付きの補正を導入し、

\nabla_\theta \mathcal{L}_{\mathrm{DFT}}(\theta)
= \nabla_\theta \mathcal{L}_{\mathrm{SFT}}(\theta)\cdot \mathrm{sg}\!\left(\pi_\theta(y^\star \mid x)\right)

の形で実装可能であると示しています。この「一行の変更」により、勾配分散が安定し、複数ベンチマークで標準 SFT を一貫して上回る結果が報告されています。

本プロジェクトでも、DFTを試行したところ、図1に示すようにベースモデルからは性能低下しているものの、SFTよりも高いHLEスコアを示す傾向が見られ、教師データへの過適合を緩和する効果が示唆されました。

CHORD

On-Policy RL Meets Off-Policy Experts: Harmonizing SFT and RL via Dynamic Weighting

CHORD は、SFT とオンポリシー RL（GRPO）を動的に統合する枠組みとして提案された手法です。論文中では、SFTの限界を実験的に示したのちに改善手法としてCHORDが提案されています。

SFT の限界に対する実験的指摘

CHORDの論文では、既存モデルと分布の異なるexpertデータでSFTを行うと、本来得られるはずの性能を十分に引き出せない場合があることを、学習曲線を通じて示しています。Qwen2.5-7B-Instructに対してDeepSeek-R1由来のexpertデータでSFTを行い、MATH-500の正答率を追跡した結果、図のようなshift→readapt→overfitの3段階の挙動が観測されています。

SFTによる"shift-readapt-overfit"の推移（CHORD論文より引用）

• Policy Shift: 学習序盤にexpertデータへの急激な適応が入り、既存の方策が乱れて性能が低下する。
• Readaptation Phase: expertのパターンに慣れ、性能が一度回復する。
• Overfitting Phase: さらに学習を続けるとexpertデータに過度適合し、汎化性能が低下する。

この結果から、expertデータによるSFTは新たな能力をもたらす一方で、既に獲得している有用なパターンを崩し、過学習を招きうることが示されています。

CHORDのアイデア

CHORDは、SFTを前処理の別ステージとしてではなく、オンポリシーRL（GRPO）の学習と単一の損失関数に統合する手法です。中心となるのは、次のハイブリッド損失です。

\mathcal{L}_{\text{Hybrid}}(\theta)
= (1-\mu)\,\mathcal{L}_{\text{GRPO}}(\theta)
+ \mu\,\mathcal{L}_{\text{SFT-}\phi}(\theta),

ここで$\mu$は学習ステップとともに高い値から低い値へと減衰するスケジュールで設定します。

• 学習序盤：$\mu$が大きく、$\mathcal{L}_{\text{SFT-}\phi}$の寄与が強い → expertデータに基づく安定した模倣学習を重視
• 学習後半：$\mu$が小さくなり、$\mathcal{L}_{\text{GRPO}}$が主導 → オンポリシーRLによる探索と報酬最大化を重視

このようにして、off-policyなexpert模倣からon-policyな探索へ、段階的かつ滑らかに移行させることを狙っています。

損失中の$\mathcal{L}_{\text{SFT-}\phi}$は、標準SFTにトークン確率に基づく重み付けを導入した項です。各ステップ$t$における正解トークン$y_t^\star$の確率を

p_t = \pi_\theta(y_t^\star \mid x, y_{<t}^\star)

とすると、

\mathcal{L}_{\text{SFT-}\phi}(\theta)
= - \mathbb{E}_{(x, y^\star)\sim D_{\text{SFT}}}
\left[
  \sum_{t=1}^{|y^\star|}
    \phi(p_t)\,
    \log \pi_\theta\left(y_t^\star \mid x, y_{<t}^\star\right)
\right],

\phi(p_t) = p_t(1-p_t)

と定義されます。

$\phi(p)=p(1-p)$は中間的な確率で最大になり、極端に高い/低い確率では小さくなる関数です。これにより、

• 高確率トークンの更新を抑え、既存パターンの固定化・過信を防ぐ
• 非常に低確率なノイズ的トークンの影響も抑える
• その中間にある「迷っている領域」の学習信号を強調する

という効果が得られます。

DFTはSFT勾配に$\mathrm{sg}(\pi_\theta(y_t^\star\mid x))$を掛けて低尤度トークンの更新を抑えるのに対し、CHORDのSFT項$\mathcal{L}_{\text{SFT-}\phi}$は$\phi(p)=p(1-p)$で低確率だけでなく高確率トークンの更新も抑え、中間確率の学習を強化します。

この$\mathcal{L}_{\text{SFT-}\phi}$と、動的に減衰する$\mu$を組み合わせた$\mathcal{L}_{\text{Hybrid}}$により、CHORDはexpertデータの有用性を活かしつつ、オンポリシーRLの探索能力と汎化性能を維持することを目指しています。

本プロジェクトではリソースの制約上、CHORDの実装検証は行えませんでしたが、今後機会があれば検証したいと思います。