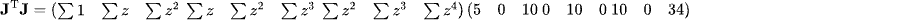ーー 滑らかにしたいけど、山の頂点だけは守りたい
信号処理の現場で何度もぶつかるジレンマを、Savitzky–Golay(SG)フィルタは驚くほどシンプルな数学で切り抜けます。鍵は「いまこの近傍だけ」を小さな多項式で近似して、その切片を取り出すこと。本記事では、そのロジックを行列の形に落とし込み、5点・2次の係数が手計算でどのように導かれるかを丁寧にたどります。仕組みを理解すれば、平滑化はもちろん、微分係数の取り出しまで自分の手で扱えるようになります。
多くの解説では「最小二乗法を使っている」という説明だけで終わってしまいますが、この記事では「実際にどのような行列計算を行って、あの有名な係数(例えば $\frac{-3, 12, 17, 12, -3}{35}$ )が導き出されるのか」を、数式を省略せずに完全に導出します。
高校数学(特に行列と微分)の知識があれば、このブラックボックスの中身を完全に理解できます。
注: “魔法のよう”と言われることがありますが大して複雑ではありません。ご安心ください。
1. 抽象的な数学モデルの構築
まずは具体的な数字を入れる前に、一般式で全体の流れ(抽象モデル)を定義します。ここをしっかり定義することで、後ほどの計算が楽になります。
1.1 問題設定:局所座標系と多項式モデル
ある時系列データ $y$ の中から、注目点(現在地)を中心に前後 $m = 2s+1$ 個のデータを切り出したとします。
計算を簡単にするため、注目点の時刻を 0 とし、データのインデックスを以下のような局所座標 $z$ に変換します。
- 座標 $z$: $\mathbf{z} = [-s, -s+1, \dots, 0, \dots, s-1, s]^T$
- 観測値 $\mathbf{y}$: $\mathbf{y} = [y_{-s}, \dots, y_0, \dots, y_s]^T$
この $m$ 個の点に対して、$K$ 次多項式 $P(z)$ を当てはめます。
$$
P(z) = a_0 + a_1 z + a_2 z^2 + \dots + a_K z^K
$$
私たちの目的は、観測データ $\mathbf{y}$ に最もフィットする係数ベクトル $\mathbf{a} = [a_0, a_1, \dots, a_K]^T$ を見つけることです。
1.2 行列による表現(Vandermonde行列)
この多項式モデルを、すべての観測点 $z$ について書き下すと、以下のような連立方程式の形になります。
$$
\begin{pmatrix}
y_{-s} \
\vdots \
y_0 \
\vdots \
y_s
\end{pmatrix}
\approx
\begin{pmatrix}
1 & (-s) & (-s)^2 & \dots & (-s)^K \
\vdots & \vdots & \vdots & \ddots & \vdots \
1 & 0 & 0 & \dots & 0 \
\vdots & \vdots & \vdots & \ddots & \vdots \
1 & s & s^2 & \dots & s^K
\end{pmatrix}
\begin{pmatrix}
a_0 \
a_1 \
\vdots \
a_K
\end{pmatrix}
$$
これをベクトルと行列でシンプルに書くと、以下のようになります。
$$
\mathbf{y} \approx \mathbf{J} \mathbf{a}
$$
ここで $\mathbf{J}$ は Vandermonde(ヴァンデルモンド)行列 と呼ばれる $m \times (K+1)$ の行列です。
1.3 最小二乗法の解(正規方程式の導出)
モデルの予測値 $\mathbf{J}\mathbf{a}$ と、実際の観測値 $\mathbf{y}$ の誤差の二乗和(残差平方和)$E$ を最小化します。
$$
E = |\mathbf{y} - \mathbf{J}\mathbf{a}|^2 = (\mathbf{y} - \mathbf{J}\mathbf{a})^T (\mathbf{y} - \mathbf{J}\mathbf{a})
$$
この $E$ を係数ベクトル $\mathbf{a}$ で微分して $0$ と置くことで、最小値を与える $\mathbf{a}$ を求めます。
行列の微分公式 $\frac{\partial}{\partial \mathbf{a}} (\mathbf{y} - \mathbf{J}\mathbf{a})^T (\mathbf{y} - \mathbf{J}\mathbf{a}) = -2\mathbf{J}^T (\mathbf{y} - \mathbf{J}\mathbf{a})$ を用いると:
$$
-2\mathbf{J}^T (\mathbf{y} - \mathbf{J}\mathbf{a}) = \mathbf{0}
$$
これを展開して整理すると、正規方程式が得られます。
$$
\mathbf{J}^T \mathbf{J} \mathbf{a} = \mathbf{J}^T \mathbf{y}
$$
したがって、求めたい係数ベクトル $\mathbf{a}$ は、以下の式で一発で計算できます。
$$
\mathbf{a} = (\mathbf{J}^T \mathbf{J})^{-1} \mathbf{J}^T \mathbf{y}
$$
1.4 フィルタ出力への変換(ここが重要!)
ここで求まった $\mathbf{a} = [a_0, a_1, \dots]^T$ は、多項式の係数セットです。
SGフィルタの目的は、「平滑化された値」を得ることでした。これは多項式の切片、つまり $z=0$ での値 $a_0$ そのものです。
上記の式 $\mathbf{a} = \dots$ 全体を計算する必要はなく、右辺の行列の「最初の行( $a_0$ に対応する行)」だけを取り出して $\mathbf{y}$ と内積をとればよいことになります。
これこそが、SGフィルタが「ただの畳み込み(固定係数の足し算)」で実装できる数学的理由です。
2. 具体例による完全導出:5点窓・2次多項式
では、実際に手を動かして計算してみましょう。
最も一般的な設定である 「窓サイズ 5点 ( $m=5, s=2$ )」、「2次多項式近似 ( $K=2$ )」 のケースを解きます。
Step 1: 行列 $\mathbf{J}$ を作る
座標は $z \in {-2, -1, 0, 1, 2}$ です。各行に $1, z, z^2$ を並べます。
$$
\mathbf{J} =
\begin{pmatrix}
1 & -2 & 4 \
1 & -1 & 1 \
1 & 0 & 0 \
1 & 1 & 1 \
1 & 2 & 4
\end{pmatrix}
$$
Step 2: $\mathbf{J}^T \mathbf{J}$ を計算する
$\mathbf{J}^T$($3\times5$)と $\mathbf{J}$($5\times3$)を掛け算すると、$3\times3$ の正方行列になります。
例えば、$(1,1)$成分は $1$ を5回足して $5$。$(3,3)$成分は $z^2 \times z^2 = z^4$ の総和です。
(奇数乗の和は対称性から $0$ になるため、計算が楽です)
※ $\sum z^2 = 4+1+0+1+4 = 10$
※ $\sum z^4 = 16+1+0+1+16 = 34$
Step 3: 逆行列 $(\mathbf{J}^T \mathbf{J})^{-1}$ を計算する
この行列を $\mathbf{M}$ と置きます。
$$
\mathbf{M} = \begin{pmatrix} 5 & 0 & 10 \ 0 & 10 & 0 \ 10 & 0 & 34 \end{pmatrix}
$$
逆行列を求めるために行列式 $\det(\mathbf{M})$ を計算します。真ん中の行・列が $0$ で独立しているので簡単です。
$\det(\mathbf{M}) = 10 \times (5 \times 34 - 10 \times 10) = 10(170 - 100) = 700$
次に、平滑化に必要なのは $a_0$ なので、逆行列の 「1行目」 だけが必要です。
余因子行列を使って1行目の成分を求めます。
- $(1,1)$成分: $\frac{1}{700} \times (10 \times 34 - 0) = \frac{340}{700} = \frac{17}{35}$
- $(1,2)$成分: $\frac{1}{700} \times 0 = 0$
- $(1,3)$成分: $\frac{1}{700} \times (0 - 10 \times 10) = \frac{-100}{700} = -\frac{5}{35}$
よって、逆行列の1行目はこうなります:
$$
[(\mathbf{J}^T \mathbf{J})^{-1}]_{\text{1st row}} = \left[ \frac{17}{35}, \quad 0, \quad -\frac{5}{35} \right]
$$
Step 4: 係数ベクトルを完成させる
最後に、$\mathbf{a} = (\mathbf{J}^T \mathbf{J})^{-1} \mathbf{J}^T \mathbf{y}$ のうち、$a_0$ を求めるための重み係数ベクトル $\mathbf{w}$ を計算します。
これは、先ほど求めた「逆行列の1行目」と「$\mathbf{J}^T$」の積です。
$$
\mathbf{w}^T = \left[ \frac{17}{35}, \quad 0, \quad -\frac{5}{35} \right]
\begin{pmatrix}
1 & 1 & 1 & 1 & 1 \
-2 & -1 & 0 & 1 & 2 \
4 & 1 & 0 & 1 & 4
\end{pmatrix}
$$
各要素(各観測点 $y_{-2}$ 〜 $y_2$ にかかる重み)を計算します:
- $z=-2$ ($y_{-2}$) 用: $\frac{17}{35}(1) + 0 + \frac{-5}{35}(4) = \frac{17-20}{35} = \mathbf{-\frac{3}{35}}$
- $z=-1$ ($y_{-1}$) 用: $\frac{17}{35}(1) + 0 + \frac{-5}{35}(1) = \frac{17-5}{35} = \mathbf{\frac{12}{35}}$
- $z=0$ ($y_{0}$) 用: $\frac{17}{35}(1) + 0 + \frac{-5}{35}(0) = \mathbf{\frac{17}{35}}$
- (対称性より $z=1, 2$ も同様)
これらをまとめると、求めるフィルタ係数は以下になります。
$$
\frac{1}{35} [-3, 12, 17, 12, -3]
$$
これこそが、教科書やライブラリで見かける「SGフィルタ(5点、2次)の係数」の正体です!
両端がマイナスになっている($-3$)ことで、単純な平均よりも「山の頂上を際立たせる」効果が生まれていることが数式からもわかります。
3. Pythonで答え合わせ
最後に、この手計算が正しいかどうか、Pythonを使って検証しましょう。
行列演算で係数を算出し、ライブラリ(scipy)の値と一致するか確認します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import savgol_coeffs, savgol_filter
# 数式導出の確認(計算しやすい m=5, K=2 で行う)
# 目的: 記事中の手計算が合っているか確認する
s_manual = 2
m_manual = 2 * s_manual + 1 # 5
k_manual = 2
# Vandermonde行列と射影行列の計算
z = np.arange(-s_manual, s_manual + 1)
J = np.vstack([np.ones_like(z), z, z**2]).T
Projection_Matrix = np.linalg.inv(J.T @ J) @ J.T
coeffs_manual = Projection_Matrix[0, :]
print(f"【数式確認】窓長{m_manual}, 次数{k_manual}")
print(f"手計算係数: {np.round(coeffs_manual, 5)}")
# scipyの係数と比較
scipy_coeffs_check = savgol_coeffs(window_length=m_manual, polyorder=k_manual)
print(f"Scipy係数 : {np.round(scipy_coeffs_check, 5)}")
print("-" * 50)
# グラフ描画(視覚的にわかりやすい m=17, K=3 で行う)
np.random.seed(42)
x = np.linspace(0, 4*np.pi, 200)
y_true = np.sin(x)
y_noise = y_true + 0.25 * np.random.randn(len(x))
# 簡単のため移動平均もSavGolも同じウィンドウ幅を使っていますが場合によってはこれは相応しくないです。
window_demo = 35
poly_demo = 3
y_sg = savgol_filter(y_noise, window_length=window_demo, polyorder=poly_demo)
y_ma = np.convolve(y_noise, np.ones(window_demo)/window_demo, mode='same')
plt.figure(figsize=(12, 6))
plt.plot(x, y_noise, '.', color='#dddddd', label='Noisy Data', zorder=1)
plt.plot(x, y_true, '--', color='gray', linewidth=1, label='True Signal', zorder=2)
# 移動平均
plt.plot(x, y_ma, '-', color='orange', linewidth=2, alpha=0.8, label=f'Moving Average (w={window_demo})')
# SGフィルタ
plt.plot(x, y_sg, '-', color='blue', linewidth=2.5, label=f'Savitzky-Golay (w={window_demo}, poly={poly_demo})')
plt.title(f'Comparison: Savitzky-Golay vs Moving Average\n(Window Length = {window_demo})')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
手計算係数: [-0.08571 0.34286 0.48571 0.34286 -0.08571]
Scipy係数 : [-0.08571 0.34286 0.48571 0.34286 -0.08571]
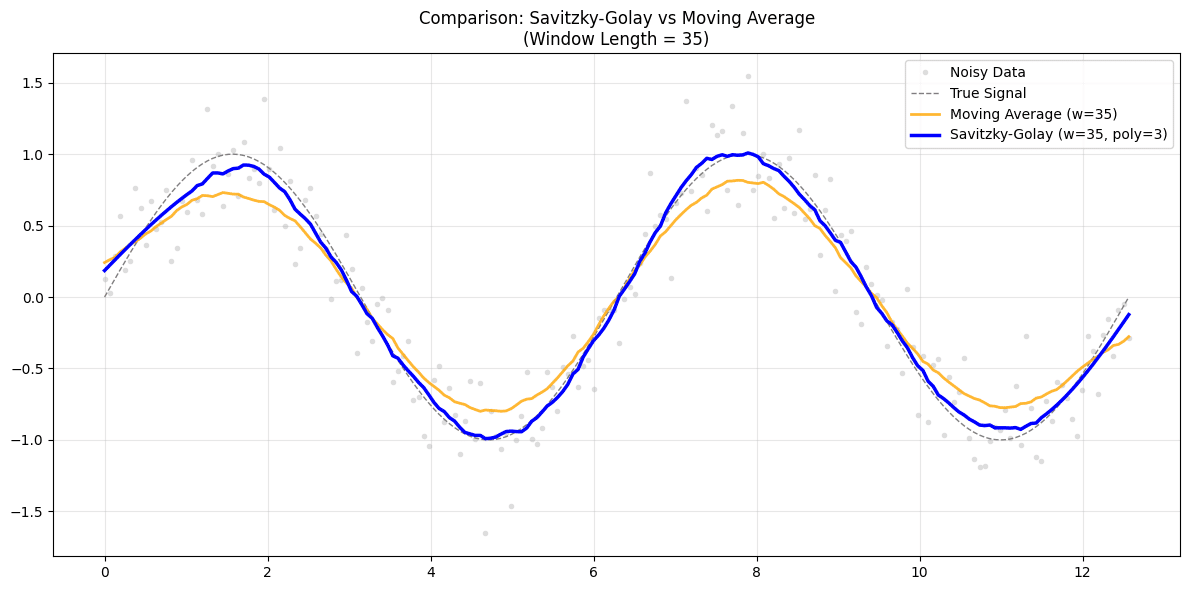
移動平均とSavGolの挙動比較。移動平均の頂点が潰れてるのに対し比較的SavGolはきれいな形状を保っている。なお、簡単のためチューニングすら実施しておらず、あくまでも参考程度だと思ってもらいたい。
結論
SGフィルタは「何か難しいことをしている」のではなく、 「局所的な最小二乗法の解を行列演算であらかじめ求めておき、それを畳み込み係数として使い回している」 という非常に合理的なアルゴリズムであることがわかりました。
この「導出過程」を知っていれば、例えば「微分の係数(速度や加速度)」が欲しいときも、上記 $\mathbf{a}$ ベクトルの2行目や3行目を取り出すだけで自分で計算できるようになります。
おすすめ
興味を持った方向け。