ニューラルネットワークを設計する上で、活性化関数(Activation Function) は極めて重要な役割を果たします。代表的な活性化関数の特徴と、学習の際によく問題となる「勾配消失」や「勾配爆発」について、図表と具体例を交えてわかりやすく解説します。
🧠 活性化関数とは?
活性化関数は、ニューロンに入力された値を変換し、次の層にどのような信号を送るかを決める関数です。これにより、モデルが非線形性(non-linearity) を獲得し、単なる線形回帰では表現できない複雑な関係を学習できるようになります。
数式で表すと、各層の出力は次のようになります:
$$
y = f(Wx + b)
$$
ここで、$f$ が活性化関数です。
🔹 代表的な活性化関数
1. Sigmoid関数
$$
f(x) = \frac{1}{1 + e^{-x}}
$$
| 特徴 | 内容 |
|---|---|
| 出力範囲 | (0, 1) |
| 長所 | 出力を確率として解釈可能 |
| 短所 | 勾配が小さくなりやすい(勾配消失) |
📊 グラフイメージ:S字カーブ(小さいxでは0、大きいxでは1に近づく)
2. tanh関数
$$
f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
$$
| 特徴 | 内容 |
|---|---|
| 出力範囲 | (-1, 1) |
| 長所 | 平均が0に近く、学習が安定しやすい |
| 短所 | Sigmoid同様、勾配消失が起こりやすい |
📊 グラフイメージ:中心が原点を通るS字カーブ。
3. ReLU関数
$$
f(x) = \max(0, x)
$$
| 特徴 | 内容 |
|---|---|
| 出力範囲 | [0, ∞) |
| 長所 | 勾配消失が起きにくく、高速に収束 |
| 短所 | x<0の領域で勾配が0(Dead ReLU問題) |
📊 グラフイメージ:負の部分は0、正の部分は直線的に増加。
4. Leaky ReLU関数
$$
f(x) = \begin{cases}x & (x>0)\ 0.01x & (x \le 0) \end{cases}
$$
| 特徴 | 内容 |
|---|---|
| 改善点 | ReLUの欠点(負の領域で勾配0)を緩和 |
📊 グラフイメージ:負の領域でもわずかに傾きがある。
5. Softmax関数
$$
f(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}
$$
| 特徴 | 内容 |
|---|---|
| 用途 | 多クラス分類の出力層 |
| 特徴 | 出力を確率分布として解釈可能 |
📊 グラフイメージ:各クラスのスコアを0〜1に正規化し、合計1となる。
⚠️ 勾配消失(Vanishing Gradient)とは
現象
ニューラルネットワークが深くなると、逆伝播(backpropagation)で伝わる勾配が次第に小さくなり、重みがほとんど更新されなくなる問題です。
原因
- Sigmoidやtanh関数のように、出力が飽和領域(0や1付近)に入ると微分値が非常に小さくなる。
- それが層を通して伝播することで、指数的に小さくなってしまう。
📉 例:
もし各層で勾配が0.1倍になると、10層で $(0.1)^{10} = 10^{-10}$ にまで減衰。
対策
- ReLUやLeaky ReLUを使用
- Batch Normalizationの導入
- 適切な初期値(Xavier, He初期化など)
⚡ 勾配爆発(Exploding Gradient)とは
現象
逆に、勾配が指数的に大きくなりすぎて学習が不安定になる現象です。
原因
- 重みが大きく、誤差が一気に増幅される
- 再帰型ネットワーク(RNN)で特に発生しやすい
対策
- 勾配クリッピング(Gradient Clipping)
- 重みの正則化(L2正則化)
🧩 簡単なPython実装例
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5, 5, 200)
# 各活性化関数
sigmoid = 1 / (1 + np.exp(-x))
tanh = np.tanh(x)
relu = np.maximum(0, x)
leaky_relu = np.where(x > 0, x, 0.01*x)
# プロット
plt.figure(figsize=(8,5))
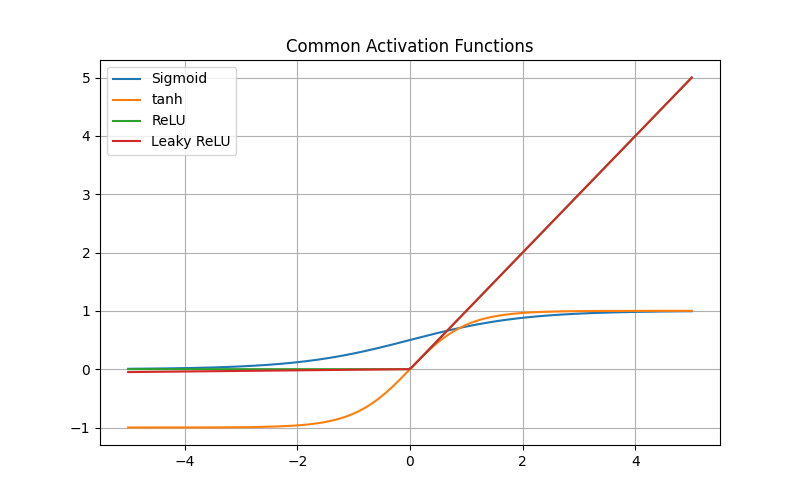
plt.plot(x, sigmoid, label='Sigmoid')
plt.plot(x, tanh, label='tanh')
plt.plot(x, relu, label='ReLU')
plt.plot(x, leaky_relu, label='Leaky ReLU')
plt.legend()
plt.title('代表的な活性化関数')
plt.grid(True)
plt.show()
📘 まとめ
| 現象 | 原因 | 主な対策 |
|---|---|---|
| 勾配消失 | Sigmoid/tanhの飽和領域 | ReLU, BatchNorm, 初期化改善 |
| 勾配爆発 | 大きな重み伝播 | 勾配クリッピング, 正則化 |
活性化関数の選択は、モデルの性能や学習速度に大きく影響します。ReLU系関数は現在でも多くのネットワークで標準ですが、タスクに応じて適切に使い分けることが重要です。