この投稿の目的
オライリーの『実践コンピュータビジョン』(以下文献[1])の多視点幾何に関する項(5章)をベースに、特に後半の説明や補足をまとめている。[1]をベースにコード以外の部分について、まとめと補足情報を書く。理解が甘い部分もあるので、追々さらに調べるつもり。
多視点による3次元構造の復元
多視点、つまり、複数の画像から([1]では2画像から)3次元を復元することを、複数のカメラの動きからの3次元構造の復元と捉えて、SfM(Structure from Motion)という。理論を深く理解していなくても、以前からよくSfMの話題では利用されているBundler(Rubyのツールじゃないよ)やGUI付きのVisualSFM、その他多視点幾何に特化したライブラリのOpenMVG、最近では、OpenCVの3.1に追加されたSfMモジュールなどを使えば、比較的容易にできるようになってきている。
多視点としているが、ここでの説明は2視点のもので、2視点以上を利用する場合の手法については補足をつけておく。
キャリブレーション済みの2つのカメラからの画像を利用する場合の[1]に示されている手順は以下の通り。
- 画像間の特徴点の対応付け
- 基礎行列の計算
- 基礎行列からのカメラ行列計算
- 3次元点の三角測量
基礎行列の推定
2画像間の特徴点を検出して、対応付けることで、エピポーラ制約で示される基礎行列(F行列)を求めていく。エピポーラ制約やエピポーラ方程式については、[1]の5章前半にまとめられているので、そちらをじっくり理解する必要があるが、ここは前提となる説明を簡単にしておく。
基礎行列と基本行列
ここでの3次元の復元はキャリブレーション済みのカメラからの画像を用いることになっている。キャリブレーション済みというのは、カメラの内部パラメターによってカメラ画像の座標系が正規化されていることを指す。この正規化されている基礎行列のことを指して、特に基本行列と呼んでいる。
- 基礎行列:カメラの内部パラメター、カメラの位置・姿勢が含まれる、カメラの位置関係を示す行列
- 基本行列:内部パラメターによるキャリブレーション済みで、カメラの位置・姿勢のみが考慮される行列
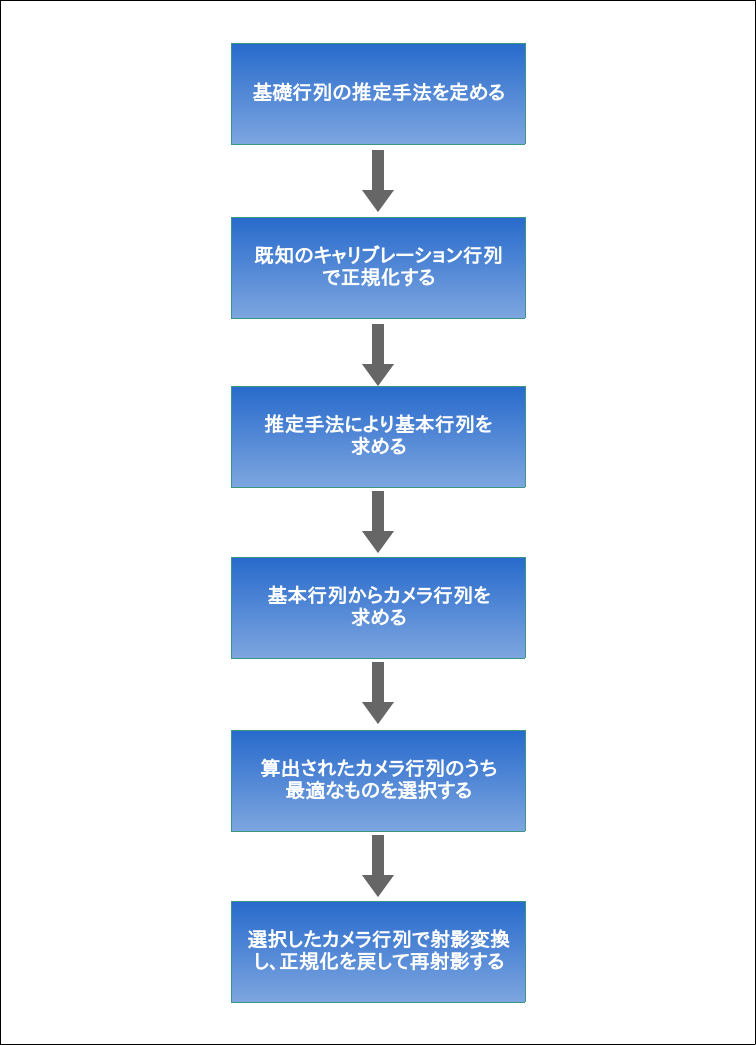
基礎行列・基本行列を考慮した復元の流れ
基礎行列と基本行列を推定しつつ、手順の2~3を行う流れについては、大まかに以下のようになる。
ここでのロジックは一旦基本行列を経由して復元する流れになっているが、基礎行列を直接分解する手法もあるようなので、さらに調べてみるとよいかも(追々やる、かも)。
基礎行列を推定するロジック
基礎行列を推定するのには、単純な線形推定含め、いくつかの方法があるが、[1]ではノイズや誤対応がある場合にも有効な推定ができるようにするために、RANSACと8点法を組み合わせたものを利用している。8点法については、[1]の5章の前半に説明されているので、詳しくはそちらに譲るが、以下の通りエピポーラ制約の線形方程式として表される。
\begin{pmatrix}
x^1_2x^1_1&x^1_2y^1_1&x^2_2w^1_1&\cdots&w^1_2w^1_1\\
x^2_2x^2_1&x^2_2y^2_1&x^2_2w^2_1&\cdots&w^2_2w^2_1\\
\vdots&\vdots&\vdots&\vdots&\vdots\\
x^n_2x^n_1&x^n_2y^n_1&x^n_2w^n_1&\cdots&w^n_2w^n_1
\end{pmatrix}
\begin{pmatrix}
F_{11}\\
F_{12}\\
F_{13}\\
F_{21}\\
F_{22}\\
F_{23}\\
F_{31}\\
F_{32}\\
F_{33}\\
\end{pmatrix}
=Af=0
基礎行列Fの成分は3x3で9つになるが、スケールを任意とすることができるので8つの対応点の計算で求まる。$\begin{vmatrix}\begin{vmatrix}Af\end{vmatrix}\end{vmatrix}$を最小化するように特異値分解で解いていく。
RANSACについては[1]の3章で扱っているので、詳しくはそちらを参照するとして、ここで行っているのは、8点法との組み合わせなので、8つの対応をランダムに選択し、いったん基礎行列を推定、推定した基礎行列をすべての対応点に適応してみて誤差を出し、指定した閾値以下の誤差であれば候補として残しておき、残った候補のうち最もよく適合したものを採用する。8つの点を選ぶ対象となる点群は、点群の重心を原点とし、平均が0、分散が1となるように予め正規化しておく。
誤差の尺度にはSampson距離を使っている。Sampson距離は幾何学的な距離の一次近似となるものだが、ここでは詳しくは踏み込まない(Sampson誤差・距離など諸々の説明を別エントリでまとめるつもり)。式だけ示しておくが、式としては[1]でも参考文献として上げている[2]のp.287あたりに上がっている
\sum_i\frac{(x'^T_iFx_i)^2}{(Fx_i)^2_1+(Fx_i)^2_2+(F^Tx'_i)^2_1+(F^Tx'_i)^2_2}
となる。さらに細かい説明や導出の部分を詳しく知りたい人は[2]を読むとよい。
ちなみに[1]のこの節で8点法は1枚の平面上にすべての特徴点がある場合は破綻すると書かれているが、それについては、そもそも2つのカメラの視点で、うち一つのカメラから見えている3次元点を、もう一方のカメラから見ているときにその点がとりうる軌跡であるエピポーラ線に対応させるための処理(点を線に対応させる)なので、そのどちらもが同じ平面上にあるとそもそも対応付けができず破綻するという認識でいる(けど、もう少しちゃんと説明はできるはずだが、細かくは参考文献など参照)。
4つのカメラ行列解からの選択と3次元点の描画
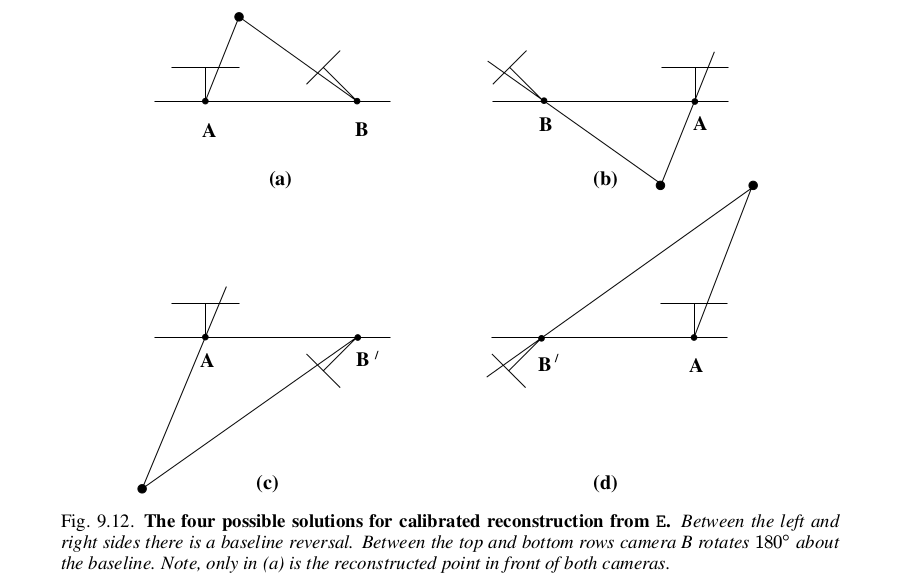
RANSACと8点法を組み合わせた基礎行列の推定ロジックと、既知のキャリブレーションを使って、基本行列を求めたあとは、そこからカメラ行列の解を得る。第1のカメラ行列は正規化されているので、ここで得られるカメラ行列の解は、第2のカメラの位置と姿勢の組み合わせで4つの解が求まることになる。下図の通り。
うち、2つのカメラの前にすべての点が来るようなカメラの位置と姿勢のものは1つだけとなる(この図の場合は(a)の位置と姿勢)。
[1]で行われている実装では、カメラ行列の選択にはRANSACでの基本行列推定時に採用した3次元点について、第1のカメラのカメラ行列と求められた第2のカメラ行列4つのそれぞれを適応して三角測量を行い、4つのうち最も大きな正の奥行き値(カメラ正面の点)が得られたカメラ行列を採用している。
第2のカメラ行列が選択できたら、採用したカメラ行列を使って、再度3次元点を三角測量し、カメラの背面に回ってしまうような点は排除しておく。ノイズや誤差点を排除した点群を射影変換し、さらにキャリブレーションの正規化を元に戻して表示することになる。
多視点での拡張を行うには?
多視点での3次元復元精度の保ち方や精度を上げるための手法がいくつかあるが、[1]に示されている範囲に留める。
視点を増やす
[1]では、動画と静止画をそれぞれ利用した手法について述べられている。
動画については、ある特徴点に注目した時に、その特徴点のフレーム毎の時間的変化に着目して3次元構造を復元する。時間経過毎に特徴点の移動を追跡していくことになるが、これには[1]の10.4節で説明されているオプティカルフローなどを応用することになる。オプティカルフローは画像中の物体の動きをベクトル化して表現するが、いくつかの推定手法を用いてベクトル化を行うことになる。

オプティカルフローのイメージ OpenCVのTutorialから引用 http://docs.opencv.org/master/d7/d8b/tutorial_py_lucas_kanade.html#gsc.tab=0
また、静止画を利用する場合についても、いくつか言及されているが、参考として、特に3視点の場合には、3焦点テンソル(Trifocal Tensor)を利用する方法がある(三重線形拘束と3視点4平面交差による処理)。[1]にある通り、文献[2]に詳細が説明されているので、興味がある場合はそちらを読むか、3焦点テンソルや三重線形拘束あたりで検索をすると、諸々出てくるはず。
バンドル調整
多視点拡張というよりは、それに伴うカメラパラメータの最適化を行うことと捉えるべき。カメラ行列や復元した3次元点は、いくつかの推定を経て得られたものなので、誤差が生じる。視点を増やすと、その誤差の累積がさらに増えていくため、最終的に得られる復元結果の誤差が大きくなってしまう。そのため、それらを調整するために、計算の結果復元した3次元点と観測値の誤差が小さくなるようにカメラの内部・外部パラメータ、3次元点それぞれを再探索していく。レーベンバーグ・マカート法を用いた手法などがよく見られるが、詳細については、[1]で示される参考文献か、岡山大学の金谷健一先生やその研究室の方の研究を検索すると、いくつか説明が出てくるので、そちらを参考にするとよい(例えば文献[3])。
自己キャリブレーション
画像の特徴点からカメラのキャリブレーションを行う各手法のこと。よくあるチェスボードを利用したキャリブレーションなども、平面上に存在する物体の特徴点を利用した手法(Zhangの手法)などいくつもの手法が提案されている。何か実際のシステムに組み込んでカメラを利用したものを実装する際には、利用するライブラリなどに依存して採用されているキャリブレーションの手法も変わってくるかもしれないが、理論的に個々の手法に興味がある場合は、参考文献等をあたるとよい。
ステレオ画像
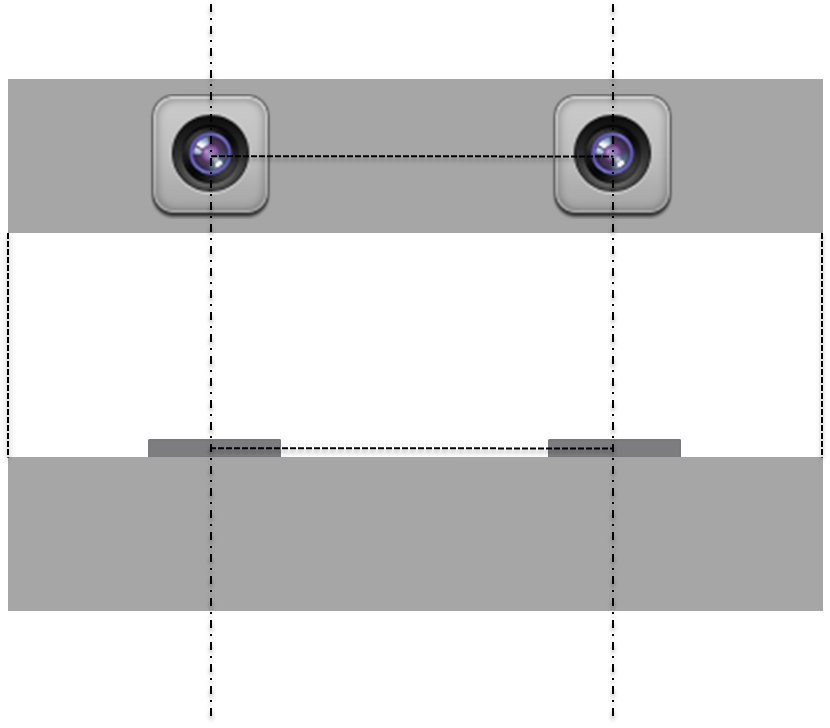
ステレオ画像は、多視点画像の中で、特に2つのカメラの捉える画像が同じ画像平面上にあって、高さが揃うように変形されていて(平行化)、エピポーラ線が画像と水平になるようにした状態で、2つのカメラの水平方向のズレから画像上の3次元点の位置と奥行き情報(ピクセル毎)を復元していく手法になる。ロボットに載せられるカメラや単体で入手できるステレオカメラなどは、カメラを平行化配置してある(ステレオリグ)。例えばこんな感じ。
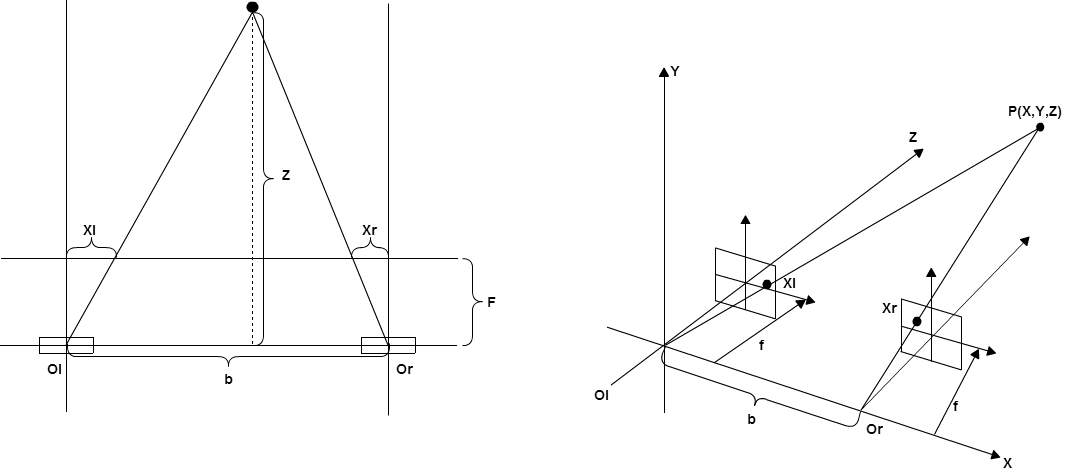
[1]のP.125では奥行き情報のみの表現をしているが、実際には、ある点$P(X,Y,Z)$について、それぞれ以下の式が成り立つ。
Z=\frac{fb}{x_l-x_r}, X=\frac{Z}{f}x_r, Y=\frac{Z}{f}y_r
fは画像の焦点距離でbはカメラ中心間の距離で、どちらも定数となり、$X,x_l,x_r$の軸は左カメラから右カメラの焦点への軸に揃っている状態となっている。
上面から見た時と、上の式で考えた左カメラを基準として3軸を取った場合はこのような関係になっている。
視差マップの作成
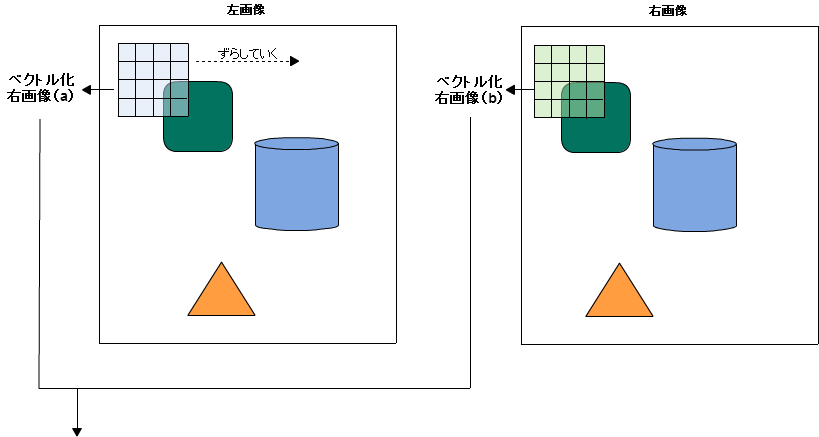
ステレオ画像による3次元復元の手順の基本は、画像1(左を基準にする場合は左画像)のある点について、画像2(右画像)を走査し、各点ごとに周辺画像の評価をしながら視差計算を行って、視差マップを作っていく。
ベクトル間の相関から各点の最適視差(奥行き)を得る
[1]では評価関数にNCC(正規化相互相関)を利用しているが、それ以外にも、以下のようなものもある。
- SSD(Sum of Squared Defferences):差の二乗和を取る単純な手法。ノイズや外光変化に弱い。
- SAD(Sum of Absolute Defferences):画素枚の差の絶対値の総和を取る手法。SSDよりノイズに強い。
[1]で行っているNCCを利用した方法では、ターゲットとする点の近傍を含む局所パッチをベクトル化し、ベクトル間の相関を取って最良の奥行きを選択している。左画像のパッチを右方向に移動させながら、右画像のパッチと相関を取るような手順となっている。
[1]ではその他に計算の効率化を行うためにガウシアンフィルタなどを適用しているが、適宜このあたりのフィルタも参考にして、適用するとよい。
【参考文献】
[1]Jan Erik Solem著 相川 愛三訳『実践コンピュータビジョン』オライリー
[2]R.I. Hartley, A. Zisserman:『Multiple View Geometry in Computer Vision』
[3]岩元 祐輝,菅谷 保之,金谷 健一(2011)「3 次元復元のためのバンドル調整の実装と評価」情報処理学会研究会報告
[4]和歌山大学講義資料 http://www.wakayama-u.ac.jp/~wuhy/CV08.pdf
[5]Marc Pollefeys: "Visual 3d modeling from images -tutorial notes" http://www.cs.unc.edu/~marc/tutorial.pdf