ミニマックス法とは
うぃきぺでぃあさまによると、「想定される最大の損害が最小になるように決断を行う戦略のこと」だそうですよ。
チョットナニイッテルカワカンナイ(´・ω・`)
あちこち検索すると・・・
自分の手番の時には、空いているマスの中で自分にとって一番有利(評価値が最大(MAX))な場所に打ち、相手の手番の時には、相手は相手にとって一番有利な場所、つまり自分にとっては一番不利(評価値が最小(MIN))になる場所へ打ってくるだろうと仮定する。
・・・ということラシイ。
互いに最善を尽くすってことですよね。
ゆってるコトはフツーなんですけれどね。
それを、どうやってプログラムにするというのか?
一番有利な場所ってどこ~。評価値って何~~~。
やってみる!
ま、どうせ考えたって分かんないんですよ。頭悪いんで><
というわけで、分かんないけどやってみます!
主に、ここを参考にしてやってみました。
海外では、Tic Tac Toeとか言うラシイ。
ここは、ゲーム木?が実際のゲーム画面を使って説明されていて、分かりやすかったです。
日本では先手が⭕、後手が❌というのが一般的だと思いますが、海外では先手が❌っぽくってちょっとコンランしたりもしましたが、実際には、先手とか後手とか⭕か❌かということは関係なくて、そこがCOMの手番なのか人間の手番なのかということだけ考えれば良いのでした。
ともかくこちらのご説明どうりにやっていきますです。
得点
評価値なんて聞き慣れないこと言われると目が回ってしまうけど、得点と言い換えただけでなんだか親しみやすいですよね^^
マルバツゲームは最大9手しかないので終局まで全部読み切って、自分が勝ったら得点をもらえて、負けたら失い、引き分けなら変わらず、というのがそのまま評価値に出来るんですね。
これはコンピューターが打つためのものなので、「自分」はコンピューターです。
勝ったのがCOMなら10点獲得、人間なら-10点。引き分けなら0点。
こんな感じ?
●(勝敗で)得点計算
勝敗で条件分岐。
COMならば、10で戻る。。。
人間ならば、-10で戻る。。。
引き分けならば、0で戻る。。。
ここまで
ここまで。
カンタンですね☆
ここで、COMと人間という変数ですが、中身は0か1が入っています。
0は先攻であり⭕、1は後攻であり❌を意味していて、ゲームの最初に先攻後攻決めをおこなって、それで決まったものをそれぞれに代入しています。
ゲーム中は、手番が0と1と交互に入れ替わりながら進むので、それで今の手番がコンピューターなのか人間なのか分かるって寸法です。
ミニマックス
うーん、こんな感じ・・・?
いちおう、参考サイトのご説明どうりにしてみたつもりなんですが・・・
●(仮手数で局面の)良手探索
着手リスト=空配列。得点リスト=空配列。仮手番=仮手数%2。
着手可能マス=局面の着手可能マス確認。
もし、手数=8ならば、次着手=着手可能マス。
# ゲームが終わる場合、COM側から見た得点を返す
結果=局面の勝敗判定。
もし、結果が継続でなければ、結果で得点計算して戻る。
# そうでない場合、着手可能なマス全てについて新たなゲーム状態のリストを取得する
着手可能マスを反復
着手候補=対象。仮盤面=局面を配列複製。
仮盤面[対象]=仮手番。
得点=仮手数+1で仮盤面の良手探索。 # 再帰
得点リストに得点を配列追加。 # その状態のミニマックスの結果を追加する
着手リストに着手候補を配列追加。
ここまで。
もし、得点リスト=空ならば、戻る。
# COMの番であれば、得点リストから最大点数を返す
もし、仮手番=COMならば、
番号=得点リストから(得点リストの配列最大値)を配列検索。
次着手=着手リスト[番号]
得点リスト[番号]で戻る。
# 人間の番であれば、得点リストから最小点数を返す
違えば、
番号=得点リストから(得点リストの配列最小値)を配列検索。
次着手=着手リスト[番号]
得点リスト[番号]で戻る。
ここまで。
ここまで。
あってる?
その局面で着手可能な全てのマスについて、そのマスに着手した場合の仮の盤面を作成して仮の手数を進め、また、その盤面で着手可能な全てのマスについて・・・と、そのルートが終局するまで自分を呼び出し続けるワケですよね。(再帰関数)
良手探索関数が返すのは得点なんですが、得点リストと同時に着手リストも作っておいて、同じ番号で最良の着手が分かるようになってます。
図解
参考サイトの説明でもなお、ワタシにとって分かりにくかった部分をワタシにとって分かりやすく描き直したものです。(先手は⭕ということにしています。実際に反復される順番どうりに並べました)
万人にとって分かりやすいかどうかは不明;
でも、他人が描いた絵をうーむと眺めているより、自分で描いてみたら分かってくる気がする。
最初のが実際の局面で、これについてどこに打ったら良いか考える。
考えられるa、b、cの着手先を反復して良手を探索していく。
(アルファベットムリとか言いながらabcかよとか言わないで~w
三文字以下のアルファベットは記号として機能します!
イロハや甲乙丙では、ナニカの法的文書みたいになって、それはそれで・・・www)
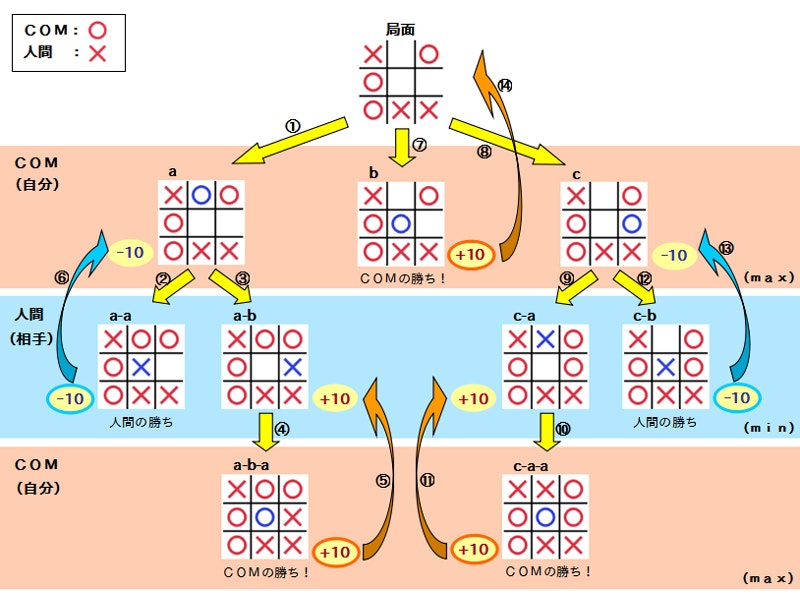
① aの場合の仮盤面を作って勝敗判定します。まだ終局ではないので手番交代して継続。
② a-aの場合の仮盤面作って勝敗判定。人間の勝ちなので、aの2段目の得点リストに**-10を追加。
③ 続いてa-bの場合の仮盤面作って勝敗判定。まだ終局ではないので手番交代して継続。
④ a-b-aの場合の仮盤面作って勝敗判定。COMの勝ち。+10**。
⑤ 着手できるのはここだけなので、それで戻ってaの2段目の得点リストに**+10を追加。
⑥ aの2段目の得点リストが揃った。人間の手番なので最小値を選択して戻り、1段目の得点リストに-10**を追加。
同様にして、b、cもチェックしていきます。
⑦ bの場合の仮盤面を作って勝敗判定。COMの勝ちなので、1段目の得点リストに**+10**を追加。
人間の考えだと、もうコレで勝てるからいいじゃんっていうところなんだけどw
⑧ cの場合の仮盤面を作って勝敗判定。
cはaの場合と似たような経過の末・・・
⑬ 1段目の得点リストに**-10**を追加。
そして・・・
⑭ 1段目の得点リストが揃った! COMの手番なので最大値(+10)を選択して、局面に戻る。 → bに着手☆
・・・みたいな?
なんか間違っていたら教えて下さい><
動作確認
前回までのコードに、上の得点計算と良手探索を追加して、レベル2を選択出来るようにしてみます。
●レベル2
手数で局面の良手探索。
次着手へ打つ。
ここまで。
とりあえずこんな感じで、今日のところはここまで。
レベルは、入力せずにOKでもレベル2になります。
ワタシが間違えてなければ現段階でも絶対に勝てない・・・ハズ・・・です。
つづきます
最終的な勝ち負けだけではなく、出来るだけ良いゲームをするため、さらにミニマックスを改良します。
っていうか、今日中にそこまで行けたと思うけど、説明できるような柄じゃないんで丸投げで済ますつもりだったミニマックスの図解を結局書いて力尽き結構長くなったのと、①冒頭の予告どうり書くことがぴんちなので、また明日~w
カレンダーまだいっぱい空いてます。みなさんご参加下さいお願いしますぅ。