CIE 関連の色空間について

国際照明委員会 (CIE, Commission internationale de l'éclairage) が定めた色空間や、関連する色空間について、そしてそれらの間の関係性について調べたことを説明する。
主に自分がよく分かっていなかったことを中心に記した。また計算して描ける図は自分で描いた。

※ まだ執筆途中であるため、今後も情報を書き足していく

視覚を司る2つの細胞

色空間の構築の歴史は、人間の知覚の仕方の研究の歴史でもある。
人間がいかにして色を捉えるのか、そして人間が捉えることのできる色をどこまで表現できるか、という観点で各種色空間が定義されている。
人間の色の捉え方を説明するには、人間の視覚を司る細胞 (視細胞) を理解する必要がある。

視細胞には錐体細胞と桿体細胞の2種類がある。

• 錐体細胞 (Cone Cell)
  • 色を感じ取る細胞
  • S, M, L の3種類が存在し、それぞれ感じ取りやすい色が異なる
  • 明るい場所でしか働かない (明所視)
    • 故に人間は暗い場所では色の違いを感じ取れない
• 桿体細胞 (Rod Cell)
  • 明るさを感じ取る細胞
  • 1種類のみ存在する
  • 暗い場所で主に働き、明るい場所では視覚に寄与しない (暗所視)
  • 錐体細胞の20倍は感度が高いとされている

以上を踏まえると、色の捉え方に一番影響を及ぼすのは錐体細胞であることがわかる。

LMS 色空間

錐体細胞の3種類 L, M, S に対応する3つの成分 $(L,M,S)$ を持った色空間として LMS 色空間というものが存在する。

各錐体細胞は、受け取る光の波長によって応答性が異なる。それぞれに対して波長 $\lambda$ に対する応答関数 (cone response functions) が定義されている。

$$
\overline{l}(\lambda)
\qquad
\overline{m}(\lambda)
\qquad
\overline{s}(\lambda)
$$

これを用いて、 LMS 色空間は次のように定義されている。

$$ \begin{alignedat}{3}
L {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{l}(\lambda)
\\
M {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{m}(\lambda)
\\
S {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{s}(\lambda)
\end{alignedat} $$

我々が目で捉える光は様々な波長の光を含んでいる。上記において $J(\lambda)$ は受け取った光に関して、波長 $\lambda$ ごとの分布 (スペクトル) を表している関数である。

各錐体細胞の感じる刺激の強さは、届いた光の波長分布と、その錐体細胞の波長に対する応答特性に依存し、それを全波長に対して足し合わせたものが、 LMS の各成分であることを上式は表している。

LMS 空間の各成分が決まると、色が1通りに決まる。
上式を使って各成分の値 $L$, $M$, $S$ から波長分布 $J(\lambda)$ を1通りに決めることは困難であることを踏まえると、上式は次のことを意味している: 1つの色に対してその色を実現する波長分布は無数に存在している。

どんな色であっても、 L, M, S の3つの錐体細胞うち1種類しか反応しないという色は存在しないので、 LMS 色空間ではおそらくどの成分も常に有限の量を持っていると考えられる。

CIE RGB 空間

錐体細胞が L, M, S でできていることや、それぞれの応答関数が分かったのは 1950 年以降だとされている。当然 LMS 色空間が登場したのもその年代以降である。
1920 年頃にはそれらの知見はないのだが、あらゆる色は3つの基本色の組み合わせで表現できることは既に知られていた。 (加法混色)

3つの基本色の選び方は色々考えられるが、 Wright は以下の組み合わせで実験を行なっていた。これらは当時光源として用意しやすかった組み合わせのようだ。

	波長	色の見た目	光源
R	700.0 nm	深赤	当時単色では再現できなかった
G	546.1 nm	緑	水銀灯
B	435.8 nm	青紫	水銀灯

• 当時 700nm 単色光を生成することは困難であったが、この近辺の波長は人間にとって見た目に違いがないために、多少ズレていても (多少混じっていても) 、結果に影響がないため採用されたという。

CIE によりこの原色定義が採用され、「あらゆる色を上記の R, G, B 光源の組み合わせにより表現しよう」として作られたのが CIE RGB 色空間である。
各成分 $(R,G,B)$ はそれぞれの光源をどれくらいの光量で混合すれば良いかを表している。

等色関数

CIE RGB 色空間でも LMS 色空間と同様の積分による表現が可能である。

$$ \begin{alignedat}{3}
R {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{r}(\lambda)
\\
G {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{g}(\lambda)
\\
B {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{b}(\lambda)
\end{alignedat} $$

$J(\lambda)$ は先ほどと同じく光の波長ごとの割合である。

一方で、 $\overline{r}(\lambda)$, $\overline{g}(\lambda)$, $\overline{b}(\lambda)$ は LMS とは意味が異なる。
これは等色関数 (color matching function) と呼ばれる関数であり、「ある波長 $\lambda$ の光に相当する色を構成するには R, G, B の3光源を $\overline{r}$, $\overline{g}$, $\overline{b}$ の割合で混ぜる必要がある」ということを意味している。
これは波長 $\lambda$ ごとに実験的に求められた値である。

応答関数	ある波長における各錐体細胞の応答の強さを表す
等色関数	ある波長の色を再現するのに必要な3成分の強さを表す

つまりこの積分は、それぞれの波長 $\lambda$ を再現するのに必要な割合 $\overline{r}$, $\overline{g}$, $\overline{b}$ が分かっているので、それを実際のスペクトル $J(\lambda)$ に応じて全波長に積み重ねていくことで、 CIE RGB の各成分が求められる、ということを表している。

CIE RGB の問題点

等色関数 $\overline{r}(\lambda)$, $\overline{g}(\lambda)$, $\overline{b}(\lambda)$ は図のように表される。

これを見ると明らかに、負の値をとる領域が存在する。等色関数が負になり得るということは、それを積分した CIE RGB も負の値をとる可能性がある。
$(R,G,B)$ は3光源の比重を示した量なので0以上の値をとることが自然であるため、負の値はおかしい。
つまり、 $R$, $G$, $B$ のいずれかが負の値を取らざるを得ない色は、そもそも選んだ3光源では表現することができない色である。言い換えれば、 CIE RGB では可視光領域のあらゆる色を表現できる訳ではない。

CIE XYZ 色空間

上記の通り CIE RGB では賄い切れない可視光領域全体をカバーするために CIE RGB を線形変換して定義されたものが CIE XYZ 色空間である。
CIE XYZ 空間は人間が捉えられる全ての色をカバーすることのできる色空間として、現代では最も基礎的な空間として位置付けられている。
CIE XYZ は CIE RGB から次の変換行列 $M_{ \mathrm{RGB} \rightarrow \mathrm{XYZ} }$ により変換される。
(行列の各成分は CIE による定義値である)

$$ \begin{gathered}
\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}
=
M_{ \mathrm{RGB} \rightarrow \mathrm{XYZ} }
\begin{bmatrix} R \\ G \\ B \end{bmatrix}
\\
M_{ \mathrm{RGB} \rightarrow \mathrm{XYZ} } =
\begin{bmatrix}
0.49000 & 0.31000 & 0.20000 \\
0.17697 & 0.81240 & 0.010630 \\
0.0000 & 0.010000 & 0.99000
\end{bmatrix}
\end{gathered} $$

上の行列成分を見ても明らかなように、 $Z$ 成分は青色に相当する成分である。また、 $Y$ 成分は輝度 (明るさ) に対応する指標である。
$X$, $Y$, $Z$ はどれも0以上の値であると想定して良い。但し上限は特にない。

逆変換は逆行列により可能である。

$$ \begin{gathered}
\begin{bmatrix} R \\ G \\ B \end{bmatrix}
=
M_{ \mathrm{XYZ} \rightarrow \mathrm{RGB} }
\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}
\\
M_{ \mathrm{XYZ} \rightarrow \mathrm{RGB} } =
\frac{1}{3400850}
\begin{bmatrix}
8041697 & -3049000 & -1591847 \\
-1752003 & 4851000 & 301853 \\
17697 & -49000 & 3432153
\end{bmatrix}
\end{gathered} $$

CIE RGB に対して等色関数が定義できたので、 CIE XYZ にも同様の等色関数 $\overline{x}(\lambda)$, $\overline{y}(\lambda)$, $\overline{z}(\lambda)$ が定義できる。
そして同じように積分の形で表される。

$$ \begin{alignedat}{3}
X {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{x}(\lambda)
\\
Y {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{y}(\lambda)
\\
Z {}={} & \int \mathrm{d}\lambda \; J(\lambda) &\; \overline{z}(\lambda)
\end{alignedat} $$

2つの色空間に対する積分を見比べると明らかであるが、等色関数自体も行列 $M_{ \mathrm{RGB} \rightarrow \mathrm{XYZ} }$ で変換される。

$$
\begin{bmatrix} \overline{x}(\lambda) \\ \overline{y}(\lambda) \\ \overline{z}(\lambda) \end{bmatrix}
=
M_{ \mathrm{RGB} \rightarrow \mathrm{XYZ} }
\begin{bmatrix} \overline{r}(\lambda) \\ \overline{g}(\lambda) \\ \overline{b}(\lambda) \end{bmatrix}
$$

新たな等色関数 $\overline{x}(\lambda)$, $\overline{y}(\lambda)$, $\overline{z}(\lambda)$ を図で示すと次のようになる。

小文字の $x$, $y$, $z$ という表記がある。これは $X$, $Y$, $Z$ を規格化したものである。

$$ \begin{gathered}
x = \frac{X}{X+Y+Z}
\qquad
y = \frac{Y}{X+Y+Z}
\qquad
z = \frac{Z}{X+Y+Z}
\\\\
\Longrightarrow \quad
x + y + z = 1
\end{gathered} $$

つまり $(x,y,z)$ は $X$, $Y$, $Z$ の割合に依存しており、 $X$, $Y$, $Z$ を一律に定数倍しても $(x,y,z)$ は変化しない。
3次元空間 $(X,Y,Z)$ のうち、大きさの情報を取り出し、向きの情報だけにしたものが $(x,y,z)$ である。 (但し $(x,y,z)$ は数学的なノルムで規格化したものではないけど)
$(x,y,z)$ の違いは色相や彩度を表しており、この定数倍の違いは明度 (明るさ) を表している。

色度図

$(x,y,z)$ の値から、対応する色相や彩度を描いた図として色度図 (Chromaticity Diagram) というものがある。
$x$, $y$ に対する直角二等辺三角形として描かれる。

この画像自体には sRGB を使用している。
後述するが sRGB は色域の一部の領域のみであり、sRGB の領域外の色は正確ではない。
sRGB の最も近い色を代用している。また輝度を調整している。

図中で色が塗られた馬蹄形の領域は色域 (ガモット, gamut) と呼ばれており、可視光全体を示す領域 (多くの人間が捉えることのできる色の全て) を示している。
曲線部分はスペクトル軌跡、下側の直線部分は純紫軌跡と呼ぶそうだ。

$x+y+z=1$ より、 $x$, $y$ の値が決まれば対応する $z$ の値が決定する。

色度図の描き方

スペクトル軌跡は、適宜曲線上に波長が刻まれていることからも分かるように、波長と対応している。
この曲線上の点は、ある単一の波長 $\lambda=l$ の光のみを捉えた場合に目で見える色を $x$, $y$ 空間上で示した点である。
そして曲線の両端は、人間の捉えられる最も長い波長と最も短い波長に対応する。

曲線上の点におけるスペクトルはデルタ関数 $J(\lambda) = \delta(\lambda-l)$ 状になっているため、以下に示すように $X$, $Y$, $Z$ は等色関数で表される。

$$\begin{gathered}
\begin{aligned}
X {}={} & \int \mathrm{d}\lambda\; \delta(\lambda-l) \; \overline{x}(\lambda) \\
{}={} & \overline{x}(l)
\end{aligned}
\\\\
\text{同様に} \quad
Y = \overline{y}(l)
\quad
Z = \overline{z}(l)
\end{gathered}$$

これを使って、この点の $x$ は簡単に求まる。

$$ \begin{aligned}
x {}={}& \frac{X}{X+Y+Z} \\
{}={}& \frac{\overline{x}(l)}{\overline{x}(l)+\overline{y}(l)+\overline{z}(l)} \\
={}& \frac{\overline{x}(l)}{s(l)} =: x_0(l)
\end{aligned} $$

最後の行で分母を $ s(\lambda) := \overline{x}(\lambda)+\overline{y}(\lambda)+\overline{z}(\lambda) $ でまとめた。
同様のことは $y$ についてもできる。

$$ y = \frac{\overline{y}(l)}{s(l)} =: y_0(l) $$

色度図における曲線部分は、人間が色を捉えることのできる波長領域に対して上に示した式で $x=x_0(\lambda)$, $y=y_0(\lambda)$ を描いていくことで出来上がる。
等色関数 $\overline{x}(\lambda)$, $\overline{y}(\lambda)$, $\overline{z}(\lambda)$ の数値データさえ用意すれば計算することで描けるだろう。これは CIE 公式サイト や Colour & Vision Research laboratory のサイト から得ることができる。
2° 観察者と 10° 観察者が選択できるが、 2° 観察者の方を選べば良い。

そして2つの波長の光 $\lambda=l_1,l_2$ を捉える場合、2つの波長の強度をそれぞれ $w_1$, $w_2$ とすれば以下のように $x$ は求められる。

$$ \begin{aligned}
X {}={}& w_1 \; \overline{x}(l_1) + w_2 \; \overline{x}(l_2)
\quad(y, z \text{も同様}) \\
\Longrightarrow\quad
x {}={}& \frac{w_1 \; \overline{x}(l_1) + w_2 \; \overline{x}(l_2)}{
\left\lbrace w_1 \; \overline{x}(l_1) + w_2 \; \overline{x}(l_2) \right\rbrace +
\left\lbrace w_1 \; \overline{y}(l_1) + w_2 \; \overline{y}(l_2) \right\rbrace +
\left\lbrace w_1 \; \overline{y}(l_1) + w_2 \; \overline{z}(l_2) \right\rbrace
} \\
{}={}& \frac{w_1 \; \overline{x}(l_1) + w_2 \; \overline{x}(l_2)}{w_1 \; s(l_1) + w_2 \; s(l_2)} \\
{}={}&
\frac{w_1 \; s(l_1)}{w_1 \; s(l_1) + w_2 \; s(l_2)} \frac{\overline{x}(l_1)}{s(l_1)} +
\frac{w_2 \; s(l_2)}{w_1 \; s(l_1) + w_2 \; s(l_2)} \frac{\overline{x}(l_2)}{s(l_2)} \\
{}={}& w_1' \cdot x_0(l_1) + w_2' \cdot x_0(l_2)
\end{aligned} $$

曲線上の点 $x_0(l_1)$ と $x_0(l_2)$ が内分比 $w_1' : w_2'$ で内分されていることが分かる。
$y$ にについても同様に
$$ y = w_1' \cdot y_0(l_1) + w_2' \cdot y_0(l_2) $$
と計算される。

3つ以上の波長 $\lambda=l_1,l_2,\dots$ がある場合についても同様に計算されて、内分であることが分かる。

$$ \begin{aligned}
X {}={}&
w_1 \; \overline{x}(l_1) + w_2 \; \overline{x}(l_2) + \cdots
\quad(y, z \text{も同様})
\\
\Longrightarrow\quad
\begin{bmatrix} x \\ y \end{bmatrix} {}={}&
w_1'' \begin{bmatrix} x_0(l_1) \\ y_0(l_1) \end{bmatrix} +
w_2'' \begin{bmatrix} x_0(l_2) \\ y_0(l_2) \end{bmatrix} + \cdots \\
\Longrightarrow\quad
w_n'' {}={}& \frac{w_n\;s(l_n)}{w_1\;s(l_1)+w_2\;s(l_2)+\cdots}
\end{aligned} $$

...ということを踏まえると、証明としてはかなり雑だが任意のスペクトル $J(\lambda)$ における $\displaystyle x = \frac{X}{X+Y+Z} $ も内分を意味しているようだ。
こうしてできる内分点はスペクトル軌跡の内側を埋め尽くす。
但し、どんな内分点もスペクトル軌跡の両端を結ぶ直線をはみ出すことはない。ゆえにこの線 (純紫軌跡) により閉じた領域が形成され、なす領域が人間の捉えられる色全体を表すことになる。

スペクトル軌跡上は単一波長のスペクトルであったが、それ以外の領域は複数の波長のスペクトルが混ざることで構成される領域である。

RGB 色空間

我々が日々使っている RGB 空間は、 CIE XYZ 空間に行列を掛けて、伝達関数 (transfer function) で変換したものである。

式で表すとこのような形である。

$$
\begin{aligned}
R {}={} & f(R_\mathrm{linear}) \\
G {}={} & f(G_\mathrm{linear}) \\
B {}={} & f(B_\mathrm{linear})
\end{aligned}
\qquad
\begin{bmatrix} R_\mathrm{linear} \\ G_\mathrm{linear} \\ B_\mathrm{linear} \end{bmatrix}
= M_{\substack{\mathrm{XYZ}\\\rightarrow\;\mathrm{RGB}}}
\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}
$$

逆にすれば

$$
\begin{aligned}
R_\mathrm{linear} {}={} & f^{-1}(R) \\
G_\mathrm{linear} {}={} & f^{-1}(G) \\
B_\mathrm{linear} {}={} & f^{-1}(B)
\end{aligned}
\qquad
\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}
= M_{\substack{\mathrm{RGB}\\\rightarrow\;\mathrm{XYZ}}}
\begin{bmatrix} R_\mathrm{linear} \\ G_\mathrm{linear} \\ B_\mathrm{linear} \end{bmatrix}
$$

2つの行列 $M_{\mathrm{XYZ}\rightarrow\mathrm{RGB}}$, $M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}}$ は、互いに逆行列である。

$$
M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}} =
{\left( M_{\mathrm{XYZ}\rightarrow\mathrm{RGB}} \right)}^{-1}
$$

RGB 空間は幾つかの種類があるが、これらの違いは伝達関数 $f(x)$ の違いと、行列 $M_{\mathrm{XYZ}\rightarrow\mathrm{RGB}}$ の違いである。
(CIE RGB も CIE XYZ との間は行列による変換だったから、広い意味では線形 RGB なのだろう)

色度図での表現

こうした RGB 空間は可視光領域の一部分を表現できるようになっている。
色度図上では RGB 空間は馬蹄形領域の一部分を占める三角形として描かれる。
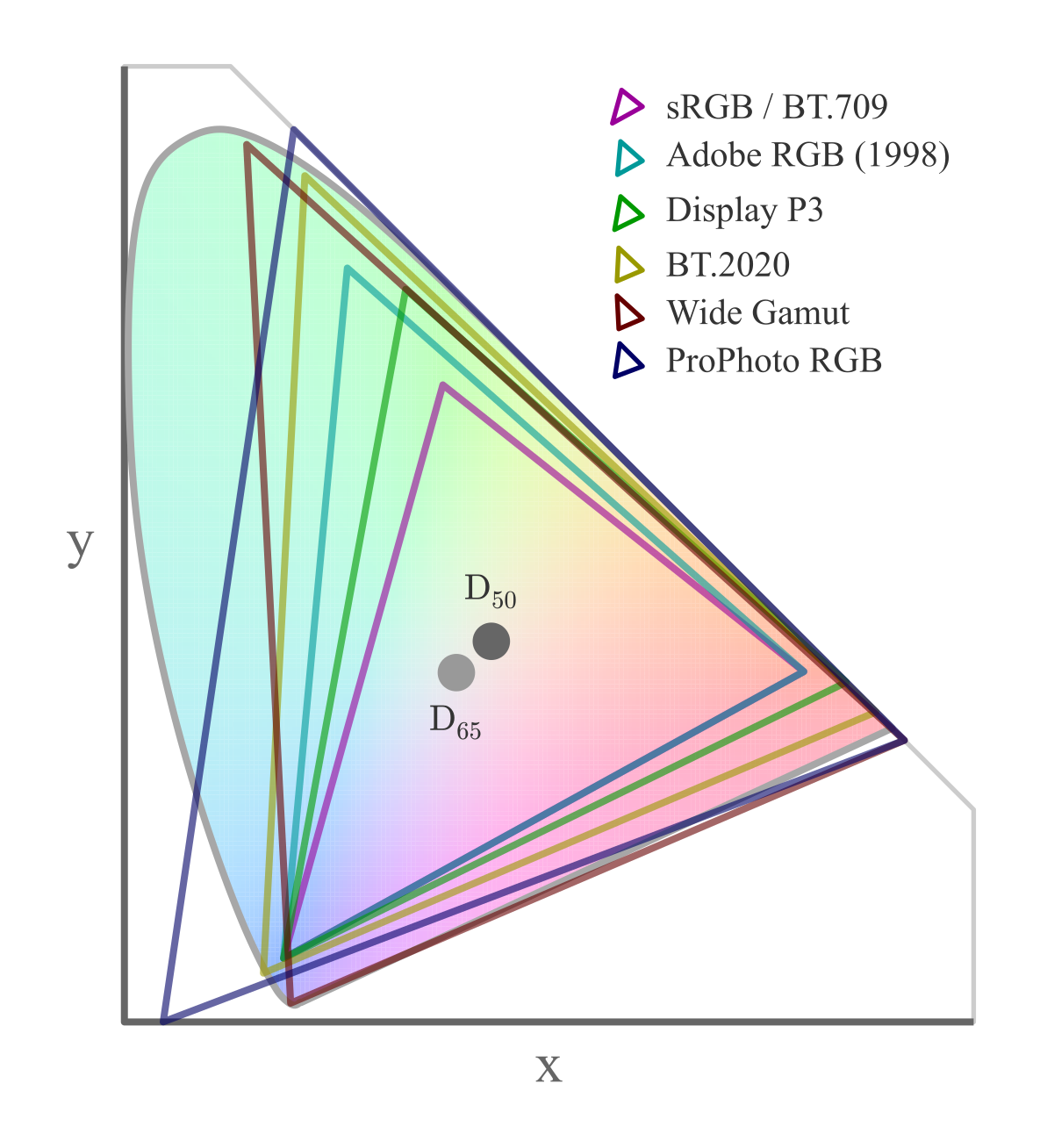
以下には RGB 色空間としてよく用いられる sRGB について、三角形を描いている。
通常ディスプレイは何かしらの RGB 空間を表示できるように作られているから、この図を見る限りディスプレイは可視光領域のごく一部分しか表示できないことが分かるだろう。

図を見る限り、 sRGB は我々の捉えられる色のうちのごく一部分しか表現することができないということがわかるだろう。
この図自体が sRGB の色空間で描かれているため、三角形内部の色は対応する色で比較的正確に描かれているものの、三角形の外側の領域は対応する色がないため、最も近い三角形内部の点の色を選んでいる。

三角形の各頂点はその RGB 空間における R, G, B に相当する色を表しており、プライマリーカラーと呼ばれる。
また、三角形の内側に示された点は、その RGB 空間における白に相当する色を表しており、白色点と呼ばれる。 (つまり白色は絶対的なものではなく、 RGB 空間によって異なる色を示している)

プライマリーカラーや白色点の RGB 空間での値は以下の通りである。
但し、 $R$, $G$, $B$ はどれも 0 ~ 1 の範囲にあるものとする。
また、 $xy$ 空間での座標を表す変数も合わせて定義する。

説明	$(R,G,B)$	$(x,y)$
プライマリーカラー (赤)	$(1,0,0)$	$(x_\mathrm{r},y_\mathrm{r})$
プライマリーカラー (緑)	$(0,1,0)$	$(x_\mathrm{g},y_\mathrm{g})$
プライマリーカラー (青)	$(0,0,1)$	$(x_\mathrm{b},y_\mathrm{b})$
白色点	$(1,1,1)$	$(x_\mathrm{w},y_\mathrm{w})$

通常 RGB 空間はプライマリーカラーと白色点の xy 座標 (+伝達関数) により規定される。

変換行列について

先程説明した、線形 RGB と CIE XYZ の間を結ぶ行列 $M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}}$ はプライマリーカラーと白色点の座標から計算することができる。

まず前にも説明したように、 $x$, $y$ は3次元空間 $(X,Y,Z)$ から大きさの情報を除いたものであり、定数倍の自由度があった。
つまり、プライマリーカラーや白色点にも XYZ 空間での表現には定数倍の自由度がある。

$$
\begin{bmatrix} X_i \\ Y_i \\ Z_i \end{bmatrix}
= L_i \begin{bmatrix} x_i \\ y_i \\ z_i \end{bmatrix}
= L_i \begin{bmatrix} x_i \\ y_i \\ 1 - x_i - y_i \end{bmatrix}
$$

$i=\mathrm{r}, \mathrm{g}, \mathrm{b}, \mathrm{w}$ とし、 $z_i := 1-x_i-y_i$ を用いた。

$ 0 \le R, G, B \le 1 $ とすれば、ある $(R,G,B)$ 値に対応する $(X,Y,Z)$ はベクトルの合成として表現できる。

$$ \begin{aligned}
\begin{bmatrix} X \\ Y \\ Z \end{bmatrix} {}={} &
R \begin{bmatrix} X_\mathrm{r} \\ Y_\mathrm{r} \\ Z_\mathrm{r} \end{bmatrix} +
G \begin{bmatrix} X_\mathrm{g} \\ Y_\mathrm{g} \\ Z_\mathrm{g} \end{bmatrix} +
B \begin{bmatrix} X_\mathrm{b} \\ Y_\mathrm{b} \\ Z_\mathrm{b} \end{bmatrix}
\\ {}={} &
\underbrace{ \begin{bmatrix}
X_\mathrm{r} & X_\mathrm{g} & X_\mathrm{b} \\
Y_\mathrm{r} & Y_\mathrm{g} & Y_\mathrm{b} \\
Z_\mathrm{r} & Z_\mathrm{g} & Z_\mathrm{b}
\end{bmatrix} }_{\displaystyle =: M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}}}
\begin{bmatrix} R \\ G \\ B \end{bmatrix}
\end{aligned} $$

$M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}}$ は上式に示されたように定義されている。あとはスケール係数 $L_\mathrm{r}$, $L_\mathrm{g}$, $L_\mathrm{b}$, $L_\mathrm{w}$ をうまく選ぶ必要がある。

CIE XYZ の Y は輝度を意味しているということから、白においては $Y=1$ であることが期待される。
そこで次のように決めてしまうことが一般的である。

$$ \begin{gathered}
L_\mathrm{w} = \frac{1}{y_\mathrm{w}}
\\\\ \Longrightarrow \quad
X_\mathrm{w} = \frac{x_\mathrm{w}}{y_\mathrm{w}}
\qquad
Y_\mathrm{w} = 1
\qquad
Z_\mathrm{w} = \frac{z_\mathrm{w}}{y_\mathrm{w}} = \frac{1-x_\mathrm{w}-y_\mathrm{w}}{y_\mathrm{w}}
\end{gathered} $$

白色では $R=G=B=1$ であることから、次の式が成立する。

$$ \begin{gathered}
\begin{bmatrix} x_\mathrm{w}/y_\mathrm{w} \\ 1 \\ z_\mathrm{w}/y_\mathrm{w} \end{bmatrix}
=
L_\mathrm{r} \begin{bmatrix} x_\mathrm{r} \\ y_\mathrm{r} \\ z_\mathrm{r} \end{bmatrix} +
L_\mathrm{g} \begin{bmatrix} x_\mathrm{g} \\ y_\mathrm{g} \\ z_\mathrm{g} \end{bmatrix} +
L_\mathrm{b} \begin{bmatrix} x_\mathrm{b} \\ y_\mathrm{b} \\ z_\mathrm{b} \end{bmatrix}
\\\\ \Longrightarrow \qquad
\begin{bmatrix} L_\mathrm{r} \\ L_\mathrm{g} \\ L_\mathrm{b} \end{bmatrix} =
{\begin{bmatrix}
x_\mathrm{r} & x_\mathrm{g} & x_\mathrm{b} \\
y_\mathrm{r} & y_\mathrm{g} & y_\mathrm{b} \\
z_\mathrm{r} & z_\mathrm{g} & z_\mathrm{b}
\end{bmatrix}}^{-1}
\begin{bmatrix} x_\mathrm{w}/y_\mathrm{w} \\ 1 \\ z_\mathrm{w}/y_\mathrm{w} \end{bmatrix}
\end{gathered} $$

ということで、この計算をすれば係数 $L_\mathrm{r}$, $L_\mathrm{g}$, $L_\mathrm{b}$ は求まり、 CIE XYZ と線形 RGB 間の変換行列 $M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}}$ が求まる。

$$
M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}} = \begin{bmatrix}
L_\mathrm{r} x_\mathrm{r} & L_\mathrm{g} x_\mathrm{g} & L_\mathrm{b} x_\mathrm{b} \\
L_\mathrm{r} y_\mathrm{r} & L_\mathrm{g} y_\mathrm{g} & L_\mathrm{b} y_\mathrm{b} \\
L_\mathrm{r} z_\mathrm{r} & L_\mathrm{g} z_\mathrm{g} & L_\mathrm{b} z_\mathrm{b}
\end{bmatrix}
$$

モノクロの表現

RGB 画像から CIE XYZ に変換した時の Y 成分だけ取り出したものがモノクロ画像である。

上記の $M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}}$ が次のように表されたとする。
$$
M_{\mathrm{RGB}\rightarrow\mathrm{XYZ}} = \begin{bmatrix}
m_{\mathrm{rx}} & m_{\mathrm{gx}} & m_{\mathrm{bx}} \\
m_{\mathrm{ry}} & m_{\mathrm{gy}} & m_{\mathrm{by}} \\
m_{\mathrm{rz}} & m_{\mathrm{gz}} & m_{\mathrm{bz}} \\
\end{bmatrix}
$$
すると $Y$ 成分は次のように求められるはずである。
$$
Y = m_{\mathrm{ry}} R + m_{\mathrm{gy}} G + m_{\mathrm{by}} B
$$
モノクロ画像の計算式はしばしば上記のように $R$, $G$, $B$ に重みをつけて足し合わせることで求められるように書かれているが、ここまでのことから分かるようにこの重みはプライマリーカラーや白色点の値から計算できる。

伝達関数について

伝達関数 (transfer function) とは撮影した映像やディスプレイに表示する映像と、記録されている映像データの間で補正を行う関数である。
つまり撮影した映像をデータにしたり、データを画面に表示する際にこうした関数で補正が行われる。

元々伝達関数が必要になったのはブラウン管ディスプレイでの表示に対応するためだったとされている。
ブラウン管では入力した電圧 $V$ に対して表示される映像の輝度 $L$ が $L \propto V^\gamma$ のようになる特性が知られている。通常は $\gamma \approx 2.2$ にしている。
そのため、表示する映像データを予め $y=x^{1/\gamma}$ で変換しておくことで、元のデータに比例する輝度が得られていた。これはガンマ補正 (gamma correction) と呼ばれ、伝達関数による変換の一種である。

最近はブラウン管ではないため、このような特性を考慮する必要は無くなったが、人間の視覚特性を表すウェーバー・フェヒナーの法則に基づいてあえて伝達関数で変換を行っている。
ウェーバー・フェヒナーの法則によれば、人間は明るい色ほど色の違いが分かりにくく、暗い色ほど色の違いが分かりやすいとされている。
色をビットを使って離散的に表現するにあたり、この法則に従って明るい色は粗く離散化し、暗い色は細かく離散化したい。
等間隔で記録されたデータを伝達関数で変換させた上でディスプレイに表示するようにすればこれが実現できる。

様々な RGB 色空間

ここまでで RGB 空間と CIE XYZ 空間の関係などについて説明してきたので、ここでは幾つかのよく使われる RGB 空間について説明し、プライマリーカラーや白色点、伝達関数について説明する。

プライマリーカラーと白色点

我々がよく用いる RGB 色空間では白色点は $\mathrm{D}_{65}$ や $\mathrm{D}_{50}$ と呼ばれる2種類に限られる。 (詳しくは後述)
それぞれの $(x_\mathrm{w},y_\mathrm{w})$ を示すと以下のような値である。

白色点	$(x_\mathrm{w},y_\mathrm{w})$
$\mathrm{D}_{65}$	$(0.31271,0.32902)$	主にディスプレイの表示に使われる
$\mathrm{D}_{50}$	$(0.34567,0.35850)$	主に印刷物によく使われる

以下に主要な RGB 空間と白色点とプライマリーカラーの座標を示す。

色空間	白色点	赤 $(x_\mathrm{r},y_\mathrm{r})$	緑 $(x_\mathrm{g},y_\mathrm{g})$	青 $(x_\mathrm{b},y_\mathrm{b})$
sRGB	$\mathrm{D}_{65}$	$(0.64,0.33)$	$(0.30,0.60)$	$(0.15,0.06)$
BT.709	$\mathrm{D}_{65}$	$(0.64,0.33)$	$(0.30,0.60)$	$(0.15,0.06)$
Adobe RGB	$\mathrm{D}_{65}$	$(0.64,0.33)$	$(0.21,0.71)$	$(0.15,0.06)$
BT.601	$\mathrm{D}_{65}$	$(0.67,0.33)$	$(0.21,0.71)$	$(0.14,0.08)$
Display P3	$\mathrm{D}_{65}$	$(0.68,0.32)$	$(0.265,0.69)$	$(0.15,0.06)$
BT.2020	$\mathrm{D}_{65}$	$(0.708,0.292)$	$(0.170,0.797)$	$(0.131,0.046)$
Wide Gamut	$\mathrm{D}_{50}$	$(0.7347,0.2653)$	$(0.1152,0.8264)$	$(0.1566,0.0177)$
ProPhoto	$\mathrm{D}_{50}$	$(0.734699,$ $0.265301)$	$(0.159597,$ $0.840403)$	$(0.036598,$ $0.000105)$
CIE RGB	$\mathrm{E}$	$\approx (0.73474,$ $0.26526)$	$\approx (0.27378,$ $0.71748)$	$\approx (0.16656,$ $0.00891)$

これらを色度図上で描くとこのようになる。

こうして見ると、いかに sRGB の色域が他に比べて小さいかがわかるだろう。 (とは言っても、この色域の違いは見分けがそんなにつくものだろうか)

Display P3

Display P3 は DCI-P3 から派生して作られた色空間である。
DCI-P3 は Digital Cinema Initiative が提唱したものであり、 sRGB などに比べて広色域に作られている一方で、白色点は 6300 K というものであった。
Display P3 では同じプライマリーカラーを持った広色域でありながら、白色点は他の多くの色空間と同じ $\mathrm{D}_{65}$ になっており、伝達関数も sRGB と同じものを使っている。

伝達関数

それぞれの色空間で利用される伝達関数は異なる。
以下にそれぞれの場合を示していくが、線形 RGB も非線形の RGB も $[0,1]$ の範囲のみを取るものとする。

sRGB, Display P3

sRGB や Display P3 では次のような途中で分岐のある関数が使用されている。線形値から非線形値を得る関数 $f(x)$ は次のように定義されている。

$$
f(x) = \left\{\; \begin{aligned}
& 12.92 \; x &\mathrm{if}\;& x < 0.0031308 \\
& ( 1 + 0.055 ) \; x^{1/2.4} - 0.055 &\mathrm{if}\;& x > 0.0031308
\end{aligned} \right.
$$
境界値 $x=0.0031308$ において2つの式で値が連続し、傾きまで一致するように作られている。

簡単のために、条件分岐なく 2.2 の冪で表されることもある。

$$
f(x) \approx x^{2.2}
$$

BT.601, BT.709, BT.2020

BT.601 や BT.709 や BT.2020 はテレビ放送や映像ファイルなどで使われているコーデックである。
BT.709 に関してはプライマリーカラーと白色点は sRGB と全く同じであるが、伝達関数だけ異なる。
線形値から非線形値を得る関数 $f(x)$ は次のように定義されている。

$$
f(x) = \left\{\; \begin{aligned}
& 4.5 \; x &\mathrm{if}\;& x < 0.018 \\
& ( 1 + 0.099 ) \; x^{0.45} - 0.099 &\mathrm{if}\;& x > 0.018
\end{aligned} \right.
$$

BT.709 と sRGB は伝達関数が異なるといっても、係数や冪指数の値が異なるだけで、関数の形はほぼ同じである。

Adobe RGB

条件分岐のない単純な冪として定義されている。

$$
f(x) = x^{256/563}
$$

ProPhoto RGB

$$
f(x) = \left\{\; \begin{aligned}
& 16 \; x &\mathrm{if}\;& x < 2^{-9} \\
& x^{1/1.8} &\mathrm{if}\;& x > 2^{-9}
\end{aligned} \right.
$$

関数形の比較

共通化

sRGB で使われるような伝達関数の逆関数を一般化して式で表すと次のようになる。

$$
f^{-1}(x) = \left\{\; \begin{aligned}
& \frac{x}{k} &\mathrm{if}\;& x < x_0 \\
& {\left(\frac{x+C}{1+C}\right)}^\gamma &\mathrm{if}\;& x > x_0
\end{aligned} \right.
$$

2つの線が切り替わる $x=x_0$ では $f^{-1}(x)$ とその傾き (微分係数) が一致するように調整すると

$$
x_0 = \frac{C}{\gamma-1} \qquad
k = {\left(\frac{C+1}{\gamma}\right)}^\gamma {\left(\frac{\gamma-1}{C}\right)}^{\gamma-1}
$$

ということで、独立なパラメータ ( = 伝達関数を特徴付けるパラメータ) は冪指数 $\gamma$ とオフセット $C$ であることがわかる。
この逆関数として、伝達関数 $f(x)$ は次のように表される。

$$
f(x) = \left\{\; \begin{aligned}
& kx &\mathrm{if}\;& x < x_0/k \\
& \left(C+1\right) x^{1/\gamma} - C &\mathrm{if}\;& x > x_0/k
\end{aligned} \right.
$$

sRGB の式と BT.709 の式はどちらもこの関数形を満たしている。
$\gamma$ と $C$ の値により伝達関数を示し直すとこのようになる。

	$\gamma$	$C$
sRGB, Display P3	$2.4$	$0.055$
BT.601, BT.709, BT.2020	$1/0.45$	$0.099$

$k$ や $x_0/k$ も上式から計算するとかなり近い値が得られることがわかるだろう。
ProPhoto RGB も $\gamma=1.8$, $C=0$ だと考えられるが、線の切り替えは $x_0/k$ では求められないし、傾き $k$ も上で示したようには得られない。

光源について

前にも説明したように、人間は明るい場所でしか色を判別できない。
しかも同じ色で表現したはずのものでも、環境の明るさによって見え方が変わってくる。故に色を説明する上では光源の違いも重要な特徴となる。
白色点とはこの光源の位置を示したものである。

CIE はこうした色を調べる上で必要な光源として標準の光 (Standard Illuminant) という光源の定義を用意してきた。
以下に主要な標準の光の定義を示す。

白色点	色温度	説明
$\mathrm{A}$	2856 K	最初に作られた光源の定義 電球色と呼ばれる、白熱電球を参考にして作られた光源。
$\mathrm{C}$	6774 K	昼間の太陽光の間接光に似せて作られた光源。 $\mathrm{A}$ の光源に対して液体フィルターを被せることで作られる。 今はその役割は後述の $\mathrm{D}_{65}$ に取って代わられた。 $\mathrm{C}$ は実際の光に比べて紫外線領域の光量が少なく、 $\mathrm{D}_{65}$ でそこが補われている。
$\mathrm{D}_{65}$	6504 K	昼光色と呼ばれる色温度領域である。 大体晴天時の正午ごろの光に近い。
$\mathrm{D}_{50}$	5003 K	昼白色と呼ばれる色温度領域である。 大体湿度の高い日の9~10時ごろの光に近い。 屋内における自然光相当の明るさでもある。
$\mathrm{E}$	~ 5500 K	全ての波長の光が等量含まれた仮想的な光を表す。

• 上記を見ても明らかなように、 $\mathrm{D}_{65}$ や $\mathrm{D}_{50}$ における添字は色温度を表している。色温度とは、温度を使って色を表現したものであり、詳しくは後ほど説明する。
• 照明はよく電球色、昼白色、昼光色という3種類で売っていることがあるが、あれらは色温度の違いを表している。他にも 3500 K 程度の温白色というものもあるらしい。 (出典: 「電球色」「昼白色」「昼光色」とは？LEDライトの種類と正しい選び方)
• $\mathrm{E}$ は全ての波長が等しく存在している場合を表す仮想的な概念である。 xy の座標は $(x,y) = (1/3,1/3)$ である。

色温度における温度の意味

あらゆる物体から電磁波が発せられている。発せられる電磁波は様々な波長のものが混じっているが、物体の温度によって電磁波の波長ごとの分布が変化することが知られている。
分かりやすい例として、通常の温度の物体だと赤外線領域の電磁波が多く発せられるため光っているように見えないが、高温の金属だと可視光域の電磁波が多く発せられるために光って見える。
高温の中でも温度が変化すれば可視光域の中で電磁波の分布は変化するので、人間に見える光の色は異なる。こうしたことから温度と色の対応付けができている。

(※ 色温度はその色を発している物体の温度を表しているのではない)

温度によるこうした電磁波の分布について定量的に記述したい。
通常の物体だと物体が発する電磁波 (輻射) の他に、物体表面での電磁波の反射も起こるため、物体の方からやってくる電磁波を説明するにはあまりにも揺らぎが大きすぎる。そこで、表面で一切反射の起こらない仮想的な物体 (黒体) の発する電磁波 (黒体輻射) について考えることとする。

こうした黒体輻射における温度、波長ごとの電磁波の分布 $I(\lambda,T)$ の仕方を記述する式として、プランクの法則がある。

$$ \begin{aligned}
I(\lambda,T)
{}={} & \frac{2hc^2}{\lambda^5} \frac{1}{\exp\left(hc/\lambda kT\right)-1} \\
{}={} & \frac{\alpha}{\lambda^5} \frac{1}{\exp\left(\beta/\lambda T\right)-1}
\end{aligned} $$

2行目は1行目における定数部分を $\alpha$, $\beta$ にまとめたものである。
それぞれの変数•定数の名称と次元をまとめると次のようになる。
次元の表し方 ... $\mathrm{E}$: エネルギー、 $\mathrm{L}$: 長さ、 $\mathrm{T}$: 時間、 $\mathrm{K}$: 温度

変数/定数	次元	名称
$\lambda$	$\mathrm{L}$	波長
$T$	$\mathrm{K}$	絶対温度
$I(\lambda,T)$	$\mathrm{E}/(\mathrm{L}^3\cdot\mathrm{T})$	分光放射輝度
$h$	$\mathrm{E}\cdot\mathrm{T}$	プランク定数
$k$	$\mathrm{E}/\mathrm{K}$	ボルツマン定数
$c$	$\mathrm{L}/\mathrm{T}$	光速
$\alpha$	$\mathrm{E}\cdot\mathrm{L}^2/\mathrm{T}$	第1放射定数
$\beta$	$\mathrm{E}\cdot\mathrm{L}\cdot\mathrm{K}$	第2放射定数

$I(\lambda,T)$ は仕事率 ($\mathrm{E}/\mathrm{T}$) を単位面積 ($\mathrm{L}^2$) あたり (面的に放射する) かつ単位波長 ($\mathrm{L}$) あたりで表した量になっている。

上記のプランクの法則の式を幾つかの温度 $T$ において $\lambda$ に対して $I(\lambda,T)$ を描いた概形は次のようになる。

ここからも明らかなように、温度が上がるとより分布が短波長寄りになっていく。つまり、赤外線よりは可視光が、可視光の中でも赤よりは青の方が増えていくことがわかる。

温度と色の対応

温度によって波長の分布が変わることがわかったので、その分布により我々の目に見える色を CIE XYZ で表現しよう。
これは前に示した等色関数 $\overline{x}(\lambda)$, $\overline{y}(\lambda)$, $\overline{z}(\lambda)$ とスペクトル $J(\lambda)$ を使って $X$, $Y$, $Z$ を表した積分式に、上記のプランクの法則で得られる $I(\lambda,T)$ を代入すれば得られる。

$$ \begin{alignedat}{3}
X(T) {}={} & \int \mathrm{d}\lambda \; I(\lambda,T) &\; \overline{x}(\lambda)
\\
Y(T) {}={} & \int \mathrm{d}\lambda \; I(\lambda,T) &\; \overline{y}(\lambda)
\\
Z(T) {}={} & \int \mathrm{d}\lambda \; I(\lambda,T) &\; \overline{z}(\lambda)
\end{alignedat} $$

そして $T$ に対する $x$, $y$ はいつも通り次の式から得られる。

$$
x(T) = \frac{X(T)}{X(T)+Y(T)+Z(T)}
\qquad
y(T) = \frac{Y(T)}{X(T)+Y(T)+Z(T)}
$$

この式により、色温度 $T$ の変化による xy 色度図上に描かれる軌跡は黒体軌跡 (Planckian locus, black body locus) という。

温度を軸に対応する色を描くと次のようになる。

これにより暖色系の色温度が低く、寒色系の色温度が高いというややこしいことが起こる。

標準の光の座標

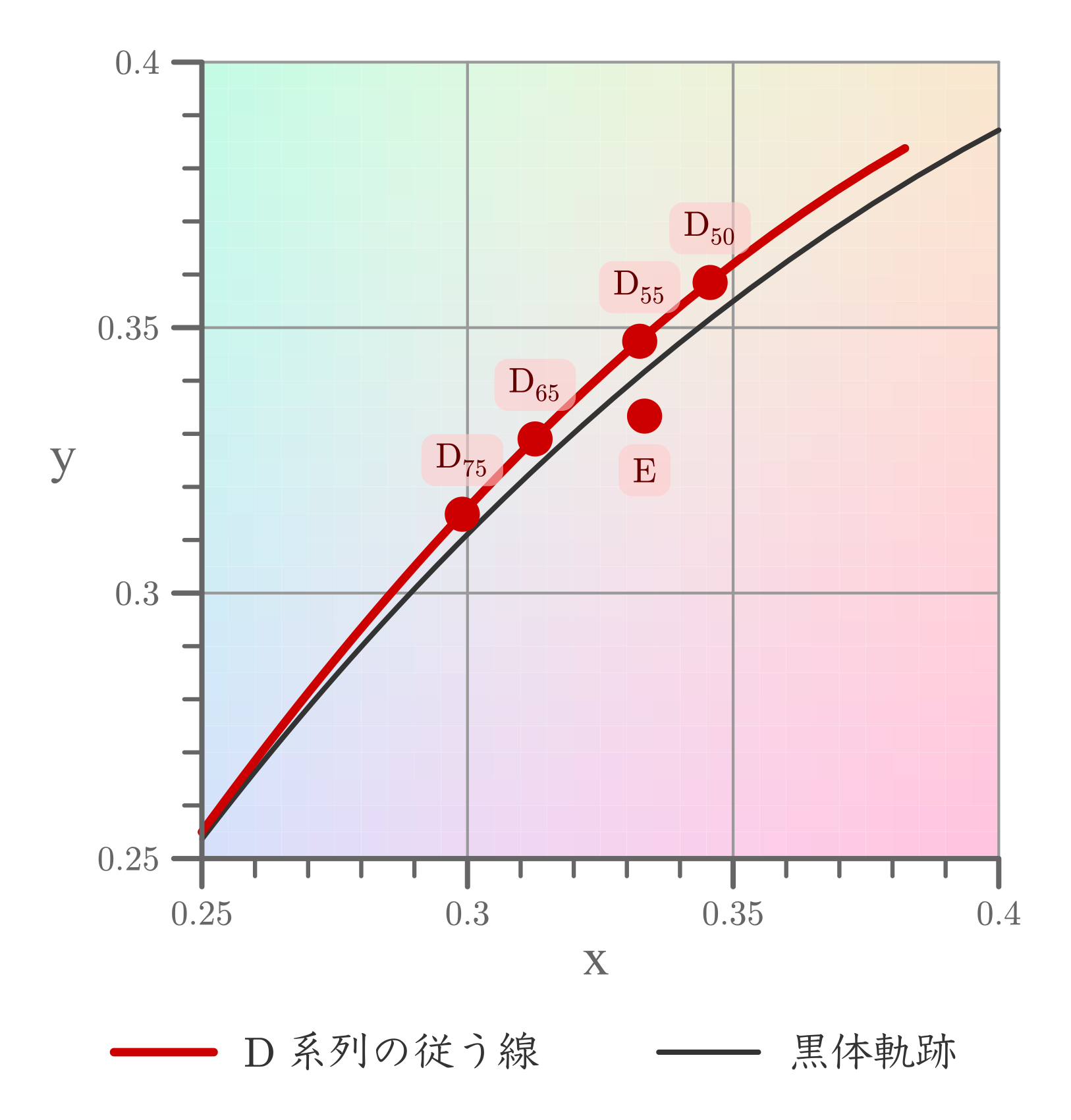
$\mathrm{A}$, $\mathrm{C}$, $\mathrm{D}_{65}$, $\mathrm{D}_{50}$ といった標準の光についても xy 色度図上での座標が決まっている。

	$(x,y)$
$\mathrm{A}$	$(0.45758,0.40745)$
$\mathrm{C}$	$(0.31006,0.31616)$
$\mathrm{D}_{50}$	$(0.34567,0.35850)$
$\mathrm{D}_{55}$	$(0.33242,0.34743)$
$\mathrm{D}_{65}$	$(0.31272,0.32903)$
$\mathrm{D}_{75}$	$(0.29902,0.31485)$
$\mathrm{E}$	$(1/3,1/3)$

これらはどれも黒体軌跡には近い位置にあるものの、黒体軌跡には載っていない。
そして $\mathrm{D}_{50}$, $\mathrm{D}_{65}$ といった D 系列の光源については、温度 $T$ に対して以下のような式で $(x,y)$ が求められることが経験的に知られている。

$$ \begin{aligned}
x {}={} & \left\lbrace \; \begin{alignedat}{8}
& 0.244063
& {}+{} & \frac{0.09911 \times {10}^3}{T}
& {}+{} & \frac{2.9678 \times {10}^6}{T^2}
& {}-{} & \frac{4.6070 \times {10}^9}{T^3}
& \qquad\mathrm{if}\quad &&
4000 \;\mathrm{K} & {}<{} & T & {}<{} & 7000 \;\mathrm{K}
\\
& 0.237040
& {}+{} & \frac{0.24748 \times {10}^3}{T}
& {}+{} & \frac{1.9018 \times {10}^6}{T^2}
& {}-{} & \frac{2.0064 \times {10}^9}{T^3}
& \qquad\mathrm{if}\quad &&
7000 \;\mathrm{K} & {}<{} & T & {}<{} & 25000 \;\mathrm{K}
\end{alignedat} \right. \\\\
y {}={} & -3.000 \; x^2 + 2.870 \; x - 0.275
\end{aligned} $$

これが図中で示した赤色の線である。
$\mathrm{D}_{50}$, $\mathrm{D}_{65}$ における下付き添字は 5000 K とか 6500 K という温度を元々示していたが、測定方法が変化したことにより、現代では 6500 K → 6504 K のように若干ずれている。以下の式で求められることが知られている。

$$
T_\mathrm{new} = \frac{1.4388}{1.4380} \times T_\mathrm{old}
$$

白色点ごとの CIE XYZ

CIE XYZ の値は白色点に依存して決められている。なので、異なる白色点の CIE XYZ 値はそのまま使い回すことはできない。
例えば $\mathrm{D}_{65}$ の RGB 空間から得た CIE XYZ の値をそのまま $\mathrm{D}_{50}$ の RGB 空間の値に使うことはできない。 CIE XYZ の中でも白色点の変換が必要である。この変換操作を色順応補正 (chromatic adaptation) とか白色点変換という。

異なる白色点の CIE XYZ を相互変換するには Bradford 変換を利用する。
Bradford 変換では CIE XYZ を LMS 色空間を挟むことで変換を行う手法である。 LMS も白色点ごとに用意されており、異なる白色点に対して LMS の各成分に対して変換可能である。

CIE XYZ と LMS の間は決まった行列によって変換される。
行列は使用される白色点によらず同じであり、具体的な行列の値はこの後説明する。

$$
\begin{bmatrix} L \\ M \\ S \end{bmatrix}
= M_{\substack{\mathrm{XYZ}\\\rightarrow\;\mathrm{LMS}}}
\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}
\qquad
\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}
= M_{\substack{\mathrm{LMS}\\\rightarrow\;\mathrm{XYZ}}}
\begin{bmatrix} L \\ M \\ S \end{bmatrix}
$$

当然ここで現れた2つの行列は互いに逆行列の関係である。

$$
M_{\mathrm{LMS}\rightarrow\mathrm{XYZ}} =
{\left( M_{\mathrm{XYZ}\rightarrow\mathrm{LMS}} \right)}^{-1}
$$

2つの LMS 色空間 $(L_1,M_1,S_1)$, $(L_2,M_2,S_2)$ の間の変換は、各成分ごとに決められた係数により変換できる。

$$ \begin{alignedat}{3}
L_2 {}={} & k_{\mathrm{L1 \rightarrow L2}} && {} \cdot {} & L_1 \\
M_2 {}={} & k_{\mathrm{M1 \rightarrow M2}} && {} \cdot {} & M_1 \\
S_2 {}={} & k_{\mathrm{S1 \rightarrow S2}} && {} \cdot {} & S_1
\end{alignedat} $$

それぞれの係数 $k_{\mathrm{L1 \rightarrow L2}}$, $k_{\mathrm{M1 \rightarrow M2}}$, $k_{\mathrm{S1 \rightarrow S2}}$ は両方の白色点 $\mathrm{W}_1$, $\mathrm{W}_2$ の値から計算できる。
白色点の xy 座標から LMS 座標を求め、これらの比を求めることで得られる。

$$ \begin{aligned}
(x_\mathrm{w1}, y_\mathrm{w1})
\quad\longrightarrow\quad
(X_\mathrm{w1}, Y_\mathrm{w1}, Z_\mathrm{w1})
\quad\xrightarrow{\; M_{\mathrm{XYZ}\rightarrow\mathrm{LMS}} \;}\quad
(L_\mathrm{w1}, M_\mathrm{w1}, S_\mathrm{w1}) \\
(x_\mathrm{w2}, y_\mathrm{w2})
\quad\longrightarrow\quad
(X_\mathrm{w2}, Y_\mathrm{w2}, Z_\mathrm{w2})
\quad\xrightarrow{\; M_{\mathrm{XYZ}\rightarrow\mathrm{LMS}} \;}\quad
(L_\mathrm{w2}, M_\mathrm{w2}, S_\mathrm{w2})
\end{aligned} $$
$$ \begin{aligned}
k_{\mathrm{L1 \rightarrow L2}} {}={} & \frac{L_\mathrm{w2}}{L_\mathrm{w1}} \\
k_{\mathrm{M1 \rightarrow M2}} {}={} & \frac{M_\mathrm{w2}}{M_\mathrm{w1}} \\
k_{\mathrm{S1 \rightarrow S2}} {}={} & \frac{S_\mathrm{w2}}{S_\mathrm{w1}}
\end{aligned} $$

CIE XYZ と LMS の間の変換行列の式

CIE XYZ と LMS の間の変換行列 $M_{\mathrm{XYZ}\rightarrow\mathrm{LMS}}$ は2種類存在する。

• Hunt-Pointer-Estevez 行列
  • 3つの錐体細胞に基づく LMS 空間の値と CIE XYZ の間の変換を行う行列
  • 実験的に求められた値
• Bradford 行列
  • 擬似的な LMS 空間と CIE XYZ の間の変換を行う行列
  • 得られる LMS は白色点の変換のためにのみ用いられる

ということで、 Bradford 変換に用いられる行列は Bradford 行列であり、この時に使用される LMS は実際の錐体細胞の知覚を反映していないものであることに注意が必要である。
2つの行列の実際の値 (近似値) は次の通り。

• Hunt-Pointer-Estevez 行列

$$
M_{\mathrm{XYZ}\rightarrow\mathrm{LMS}} =
\begin{bmatrix}
0.4002 & 0.7076 & -0.0808 \\
-0.2263 & 1.1653 & 0.0457 \\
0 & 0 & 0.9182
\end{bmatrix}
$$

• Bradford 行列

$$
M_{\mathrm{XYZ}\rightarrow\mathrm{LMS}} =
\begin{bmatrix}
0.8951 & 0.2664 & -0.1614 \\
-0.7502 & 1.7135 & 0.0367 \\
0.0389 & -0.0685 & 1.0296
\end{bmatrix}
$$

この2種類の他にも LMS の定義はあるらしいが、省略。

CIE Lab

しばしば Lab* などと表記される CIE Lab も人間の知覚に基づく色空間である。
明度を表す L 成分と、色相を表す a, b 成分からなり、 L は人間の知覚に近い。
また2つの RGB の色を合成するにあたっても、単純に各成分を線形に足し合わせるよりは、一旦 CIE Lab に変換した上で、その上で線形に足し合わせて、元に戻した方がより直感に基づく色合成ができやすい。

CIE Lab は CIE XYZ から次の式で求められる。但し、 $(X_\mathrm{W}, Y_\mathrm{W}, Z_\mathrm{W})$ は CIE XYZ で使用されている白色点の座標である。
CIE Lab は白色点座標で規格化して求めているが、 CIE XYZ と同様に白色点ごとに別物であることに注意する。

$$ \begin{alignedat}{4}
L & {} = {} & 116 & && f\left(\frac{Y}{Y_\mathrm{W}}\right) & {}-{} & 16 \\
a & {} = {} & 500 & \biggl[\; && f\left(\frac{X}{X_\mathrm{W}}\right) & {}-{} & f\left(\frac{Y}{Y_\mathrm{W}}\right) \;\biggr] \\
b & {} = {} & -200 & \biggl[\; && f\left(\frac{Z}{Z_\mathrm{W}}\right) & {}-{} & f\left(\frac{Y}{Y_\mathrm{W}}\right) \;\biggr]
\end{alignedat} $$

$f(x)$ は伝達関数のように非線形な関数である。具体的には次の式で表される。

$$
f(x) = \left\{\; \begin{aligned}
& x^{1/3} && \mathrm{if}\; x > {\left(\frac{6}{29}\right)}^3 \\
& \frac{1}{3}{\left(\frac{29}{6}\right)}^{2} \cdot x + \frac{4}{29} && \mathrm{if}\; x < {\left(\frac{6}{29}\right)}^3 \\
\end{aligned} \right.
$$

伝達関数と同じような関数形をしているが、 $𝑓(0) = 4/29 \ne 0$ になっていることに注
意する。

$L$ の値域は $[0,100]$ である。

逆変換については逆関数を導くことで得られる。

$$ \begin{alignedat}{3}
X & {}={} && X_\mathrm{W} & f^{-1} \biggl(\; \frac{L+16}{116} & {}+{} \frac{a}{500} \;\biggr) \\
Y & {}={} && Y_\mathrm{W} & f^{-1} \biggl(\; \frac{L+16}{116} & \;\biggr) \\
Z & {}={} && Z_\mathrm{W} & f^{-1} \biggl(\; \frac{L+16}{116} & {}-{} \frac{b}{200} \;\biggr)
\end{alignedat} $$

$$
f^{-1}(x) = \left\lbrace\; \begin{aligned}
& x^3 && \mathrm{if}\; x > \frac{6}{29} \\
& 3 {\left(\frac{6}{29}\right)}^2 \left(x-\frac{4}{29}\right) && \mathrm{if}\; x < \frac{6}{29}
\end{aligned} \right.
$$

CIE LCh

CIE LCh とは、 CIE Lab の色み成分である a, b について極座標化した色空間である。
これにより、 HSV などと同じく色相、彩度、明度という分け方が実現する。

RGB から Lab を求める方法

CIE Lab を RGB から求めるにあたっては、一旦 CIE XYZ を挟まなくてはならない。
さらに CIE Lab というと、通常は $\mathrm{D}_{50}$ のものを指すので、 $\mathrm{D}_{65}$ からは白色点変換が必要である。
...ということで意外と複雑である。当たり前のように Lab 空間が使われているけど、実際に計算するとなると結構面倒なのだ。

Oklab

CIE Lab に比べて線形性があり、かつ人間の視覚に合わせて最適化した色空間である。

Oklab は公式サイトで導出方法が説明されている。 $\mathrm{D}_{65}$ 白色点の CIE XYZ から求められる。
CIE XYZ に行列 $M_1$ を掛けて LMS 空間 $(l,m,s)$ に変換し、そして各成分を 1/3 乗した上で、さらに行列 $M_2$ を掛けて Oklab を得る。

$$
\begin{pmatrix} l \\ m \\ s \end{pmatrix}
= M_1 \begin{pmatrix} X \\ Y \\ Z \end{pmatrix}
\quad
\begin{pmatrix} l' \\ m' \\ s' \end{pmatrix}
= \begin{pmatrix} l^{1/3} \\ m^{1/3} \\ s^{1/3} \end{pmatrix}
\quad
\begin{pmatrix} L \\ a \\ b \end{pmatrix}
= M_2 \begin{pmatrix} l' \\ m' \\ s' \end{pmatrix}
$$

途中で用いられる行列 $M_1$, $M_2$ の値は以下のように正確に定義されている。なので、上記にある LMS 空間 $(l,m,s)$ は Bradford のものや、 Hunt-Pointer-Estevez のものとは無関係である。

$$ \begin{aligned}
M_1 {} = {} & \begin{bmatrix}
+0.8189330101 & +0.0329845436 & ​+0.0482003018 \\
​+0.3618667424 & +0.9293118715 & ​+0.2643662691 \\
​−0.1288597137 & +0.0361456387 & +0.6338517070
\end{bmatrix} \\
M_2 {} = {} & \begin{bmatrix}
+0.2104542553 & +1.9779984951 & +0.0259040371 \\
​+0.7936177850 & −2.4285922050 & +0.7827717662 \\
​−0.0040720468 & +0.4505937099 & −0.8086757660
\end{bmatrix}
\end{aligned} $$

逆変換は逆に解くだけである。

$$
\begin{pmatrix} l' \\ m' \\ s' \end{pmatrix}
= {\left(M_2\right)}^{-1} \begin{pmatrix} L \\ a \\ b \end{pmatrix}
\quad
\begin{pmatrix} l \\ m \\ s \end{pmatrix}
= \begin{pmatrix} {\left(l'\right)}^3 \\ {\left(m'\right)}^3 \\ {\left(s'\right)}^3 \end{pmatrix}
\quad
\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}
= {\left(M_1\right)}^{-1} \begin{pmatrix} l \\ m \\ s \end{pmatrix}
$$

Oklab においても CIE Lab と同じように a,b を極座標変換して得られる OKLCh という色空間がある。
色相の変化を見ると比較的「なだらか」に変化していることがわかるだろう。

CIE LCh と Oklch については HSL と色相を合わせるために 30° だけずらしている。
本来は 0° の位置によりマゼンタに近い色が現れる。