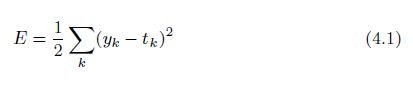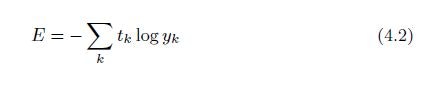「ゼロから作るDeep Learning」(斎藤 康毅 著 オライリー・ジャパン刊)を読んでいる時に、参照したサイト等をメモしていきます。 その6← → その8
そんなもんだよね、でわかったつもりでいればそれで済むことが、どうにも気になり、ひっかかって先に進めません。損失関数について、あれこれいじってみました。
4.2 損失関数
数式とか、よくわからない時は、実際に数字をあてはめてみるのが理解への近道です。
何回もやってみれば、理解できなくても納得くらいはできます。
ということで、まずは2乗和誤差から。
2乗和誤差
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [ 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
という数字を当てはめると
E = 0.5 * (
(0.1 - 0)**2 + (0.05 - 0)**2 + (0.6 - 1)**2 + (0.0 - 0)**2 + (0.05 - 0)**2
+ (0.1 - 0)**2 + (0.0 - 0)**2 + (0.1 - 0)**2 + (0.0 - 0)**2 + (0.0 - 0)**2
)
= 0.5 * (0.01 + 0.0025 + 0.16 + 0 + 0.0025 + 0.01 + 0 + 0.01 + 0 + 0)
= 0.0975
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
t = [ 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
のときは
E = 0.5 * (
(0.1 - 0)**2 + (0.05 - 0)**2 + (0.1 - 1)**2 + (0.0 - 0)**2 + (0.05 - 0)**2
+ (0.1 - 0)**2 + (0.0 - 0)**2 + (0.6 - 0)**2 + (0.0 - 0)**2 + (0.0 - 0)**2
)
= 0.5 * (0.01 + 0.0025 + 0.81 + 0 + 0.0025 + 0.01 + 0 + 0.36 + 0 + 0)
= 0.5975
# 2乗和誤差
import numpy as np
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
mean_squared_error(np.array(y),np.array(t))
0.09750000000000003
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
mean_squared_error(np.array(y),np.array(t))
0.5975
このへんあたりは、数式も理解の範囲内なので、数字をあてはめて計算して、プログラムを組んで結果を付き合わせると、なんとなく納得はできます。
正解と答えの差(距離)を集計しているんだろうな、たぶん・・・
距離を求めるときは、ピタゴラスの定理を使うとか、正負の符号をなくすためとかで2乗したよなあ、となんとなく納得したのですが、
?
2分の1?
なんで?
距離の合計という意味合いのものなら、2分の1にしなくてもいいわけだし、平均ということなら要素の数で割らないといけないわけだし・・・
なんてことを考える(と言うか、わからないと感じている)人は他にもいるようで、
こんなサイトの記事を読んで、少しだけ納得できました。
→ 線形回帰で二乗和を2で割る理由について
交差エントロピー誤差
このへんになると、logなんてものがあるので、数式そのものがいまひとつピンときません。
ただ、シグマの中は t × logy と、掛け算になっているので、
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
なら、正解の場合(1)以外のtは0なので、正解以外のt × logy はすべて0となり、
計算するのは、正解の場合だけでいいことになる。
-1 *(t × logy) = -1 *( 1 * log 0.6 ) = 0.51083
-1 *(t × logy) = -1 *( 1 * log 0.1 ) = 2.30259
# 交差エントロピー誤差
import numpy as np
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
cross_entropy_error(np.array(y), np.array(t))
0.510825457099338
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cross_entropy_error(np.array(y), np.array(t))
2.302584092994546
で、ここでの疑問は
なんで対数?
ということになるわけで、
このサイトを参考にしました。
→ 交差エントロピー誤差をわかりやすく説明してみる
で、なんとなくわかったのは、
2乗和誤差も交差エントロピー誤差も、微分されることを前提にしているらしい。
微分したときに計算しやすいように、2乗和誤差は2分の1を掛け、交差エントロピー誤差は対数を使う、ということらしい。
つまり
数学をやる人って、数式を変換するのは得意だけど、数字を計算するのは苦手(嫌い)?!
このへんのことがP155にも書かれてます。
「ソフトマックス関数」の損失関数として「交差エントロピー誤差」を用いると、
逆伝播が(y1 − t1, y2 − t2, y3 − t3) という“キレイ”な結果になりました。
実は、そのような“キレイ”な結果は偶然ではなく、そうなるように交差エント
ロピー誤差という関数が設計されたのです。また、回帰問題では出力層に「恒
等関数」を用い、損失関数として「2 乗和誤差」を用いますが(「3.5 出力層の
設計」参照)、これも同様の理由によります。つまり、「恒等関数」の損失関数
として「2 乗和誤差」を用いると、逆伝播が(y1 − t1, y2 − t2, y3 − t3) とい
う“キレイ”な結果になるのです。
おまけ
P90 のグラフを描くプログラム
import numpy as np
import matplotlib.pylab as plt
x = np.arange(0.01, 1.00, 0.01)
y = np.log(x)
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x, y)
plt.show()
このプログラムの3行目で x の値を 0.00 から始めると、
RuntimeWarning: divide by zero encountered in log
というエラーになってしまいます。
数字をあてはめて計算してみないと納得できない! という人は私だけではないようで、もっと複雑な式を手計算している人がいました。
→ニューラルネットワークの順伝播,逆伝播,確率的勾配降下法を手計算する