Python での回帰分析 --「子供にはすぐ解けて大人にはなかなか解けない問題」を例として

周回遅れも良いところだけれども，この問題：

data.dat

8809=6
3333=0
7111=0
5555=0
2172=0
8193=3
6666=4
8096=5
1111=0
7777=0
3213=0
9999=4
7662=2
7756=1
9312=1
6855=3
0000=4
9881=5
2222=0
5531=0

を pandas の線形回帰ライブラリを用いて解いてみた．

方針

それぞれの数字 $n$ には何かの特徴（まあ答えを言ってしまうと穴の数．ただしそれは今は判らないとしておく）があるものと
仮定します．それをパラメータ $\phi_n$ であらわします．例えば 0000=4 の場合，

\phi_0 + \phi_0 + \phi_0 + \phi_0 = 4 \phi_0 = 4

みたいな事になっているとします．最終的には $\phi_0 = 1$ になることが期待されますが，それを求めることが今回の
目的です．（というか，ここまでモデルを立てた時点で終わっているという話が……　まあ矛盾がないくらいの検証はしないとですね）

ということで，それぞれの列を

\sum_{n=0}^{9} k_n \phi_n = k_0 \phi_0 + k_1 \phi_1 + \cdots + k_9 \phi_9 = s

みたいな形に変形してやって，これをたくさん連立させて解けば良いと．ここまで判れば
敢えて行列にする意味もないと思うけど，試しに書いてみると，

\begin{pmatrix}
k_0^{(0)} & k_1^{(0)} & \cdots & k_9^{(0)} \\
k_0^{(1)} & k_1^{(1)} & \cdots & k_9^{(1)} \\
\vdots    & \vdots    & \ddots & \vdots    \\
k_0^{(n)} & k_1^{(n)} & \cdots & k_9^{(n)} 
\end{pmatrix}
\begin{pmatrix}
\phi_0 \\ \phi_1 \\ \vdots \\ \phi_9
\end{pmatrix}
=
\begin{pmatrix}
s^{(0)} \\ s^{(1)} \\ \vdots \\ s^{(n)}
\end{pmatrix}

ただし冪の $\cdot^{(n)}$ みたいなのは $n$ 番目の式の係数を示しています．
$k$ と $s$ たちは問題から決まるのでそのコードを書いていきます．

コード

pandas, numpy, statsmodels を読み込む

solver.py

import pandas as pd
import numpy as np
import statsmodels.api as sm

文字列から $k$ を生成する関数を定義する

問題文の左辺の文字列 question 右辺の文字列 answer から 関数 convert(question, answer)
$k$ たちと $s$ を生成して配列に格納します．
配列は左から 0 の個数（$k_0$），1 の個数 ($k_1$) ……，9 の個数 ($k_9$)，答えの数字 (s) です．

（例） convert(0042,1) = [2,0,1,0,1,0,0,0,0,0,1]

(cont'd)

def convert(question, answer):
    array = np.zeros(11)
    for char in list(question):
        array[int(char)] += 1
    array[10] = int(answer)
    return array

データを読み込み

(cont'd)

file = open("data.dat")
problems = []
for line in file:
    line = line.rstrip().split("=")
    problems.append(convert(line[0], line[1]))

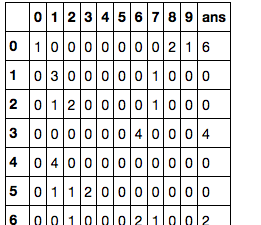
列名をつけてデータフレームを定義する

(cont'd)

name = ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "ans"]
dataframe = pd.DataFrame(np.array(problems), columns = name)

データフレームを切り出す

(cont'd)

y = dataframe["ans"]
X = dataframe[["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]]

線形回帰する

(cont'd)

model = sm.OLS(y,X)
results = model.fit()
results.summary()

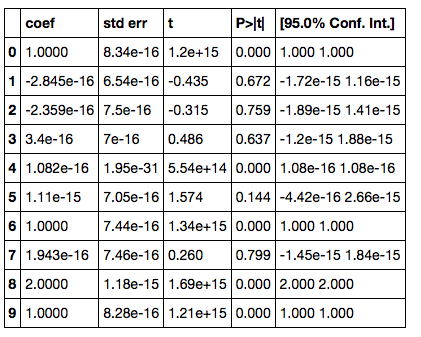
結果

いやあ．あれ？　そもそもデータには 4 が入ってないからもっと変なことが起きて欲しいんだけども，
ほぼ 0 で間違いないと言っているのはなんと言うことでしょう．
初期値をもうちょっと工夫すべきですね．　とほほ．

まとめ

Python を使って線形回帰分析をしてみました．初期値依存性とかをもうちょっと考えないといけません
．最後に全体のコードを再掲しておきます．

solver.py

# coding: utf-8
import pandas as pd
import numpy as np
import statsmodels.api as sm
def convert(question, answer):
    array = np.zeros(11)
    for char in list(question):
        array[int(char)] += 1
    array[10] = int(answer)
    return array

file = open("data.dat")
problems = []
for line in file:
    line = line.rstrip().split("=")
    problems.append(convert(line[0], line[1]))

name = ["0", "1", "2", "3", "4", "5", "6", "7", "8", "9", "ans"]
dataframe = pd.DataFrame(np.array(problems), columns = name)

y = dataframe["ans"]
X = dataframe[["0", "1", "2", "3", "4", "5", "6", "7", "8", "9"]]

model = sm.OLS(y,X)
results = model.fit()
results.summary()