強化学習の基礎まとめ

こんにちは、すきにーです。

強化学習の基礎的な手法についてまとめました。

はじめに

この記事では以下を説明しています

• 動的計画法
• モンテカルロ法
• TD法(SARSA、Q学習)

コードはゼロから作るDeepLearning4 強化学習編 に載っているものを参考にしています。

参考記事

深層強化学習アルゴリズムまとめ
ゼロからDeepまで学ぶ強化学習
これから強化学習を勉強する人のための「強化学習アルゴリズム・マップ」と、実装例まとめ
今さら聞けない強化学習（1）：状態価値関数とBellman方程式

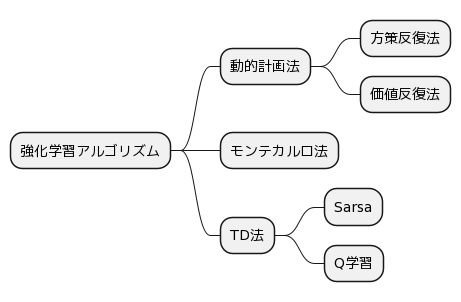
全体図

動的計画法

動的計画法は、エージェントが置かれた環境のモデルがすでに分かっているとき最適な方策を見つけるアプローチです。

方策反復法と価値反復法があります。
環境のモデルが分かっていることは少ないので、あまり使われません。

モンテカルロ法

動的計画法では環境のモデルが完全にわかっている状態で最適方策を見つけるアプローチでしたが、最初から環境のモデルが既知なことは少ないです。

環境のモデルが分からない中で実際に行動を起こして、その経験から最適な方策を決定する方法がモンテカルロ法です。
Q値の更新はエピソードが終わった後に行われます。

実装

以下はOpenAI GymのCartPoleをモンテカルロ法で実装するコードです。

import gym
import numpy as np

# 状態空間と行動空間の定義
state_space = [np.linspace(-4.8, 4.8, num=10),
               np.linspace(-5, 5, num=10),
               np.linspace(-0.418, 0.418, num=10),
               np.linspace(-5, 5, num=10)]
action_space = [0, 1]

# Q値の初期化
Q = np.zeros((10, 10, 10, 10, 2))

# ゲームの環境の設定
env = gym.make('CartPole-v0')

# エピソードの試行回数
num_episodes = 5000

# 5000回のエピソードで学習を行う
for i in range(num_episodes):
    # ゲームの初期化
    observation = env.reset()
    done = False
    episode = []

    # 1エピソードの実行
    while not done:
        # 現在の状態を取得し、離散化する
        state = [np.digitize(observation[i], state_space[i]) - 1 for i in range(4)]
        # 行動の選択
        action = np.argmax(Q[state[0], state[1], state[2], state[3]])
        # 状態と行動の保存
        episode.append((state, action))
        # 行動を実行し、次の状態と報酬を取得する
        observation, reward, done, info = env.step(action)
    
    # エピソードの終了時に、各状態と行動のQ値を更新する
    G = 0
    for t in range(len(episode)-1, -1, -1):
        state, action = episode[t]
        G = G + reward
        Q[state[0], state[1], state[2], state[3], action] += 0.1 * (G - Q[state[0], state[1], state[2], state[3], action])

# 学習後に、最適な政策を取得する
policy = np.argmax(Q, axis=4)

# 結果の表示
print(policy)

while文が終わった後にQ値が更新されてます。

モンテカルロ法の問題点

モンテカルロ法では、Q値はエピソードの終了後でないと更新できません。
そのため、現実の複雑なシステムには対応できないため、次のTD法が主流になりました。

TD法

TD法は、現在の推定値と次の状態の推定値を用いて、現在の推定値を更新する手法です。
モンテカルロ法と異なり、1ステップごとに即時報酬を受け取り、その都度に価値を更新することができます。

TD法の代表的な手法として、SARSAとQ学習があります。

SARSA

SARSAは方策オン型の手法で、 現在の状態(S)、選択した行動(A)、得られた報酬(R)、次の状態(S')、そして次の行動(A')を元にQ値を更新します。
SARSAという文字はここから来ています。

import gym
import numpy as np

# Qテーブルの初期化
Q = np.zeros((4, 2))

# ハイパーパラメータの設定
alpha = 0.1  # 学習率
gamma = 0.9  # 割引率
epsilon = 0.1  # ε-greedy法のε

# 環境の作成
env = gym.make('CartPole-v0')

# エピソード数
num_episodes = 1000

# 各エピソードの処理
for i in range(num_episodes):
    # 環境の初期化
    observation = env.reset()

    # 初期状態での行動の選択
    if np.random.uniform(0, 1) < epsilon:
        action = env.action_space.sample()
    else:
        action = np.argmax(Q[observation, :])

    # ステップ数のカウント
    t = 0

    # 1エピソードの処理
    while True:
        # 行動の実行
        next_observation, reward, done, info = env.step(action)

        # 次状態での行動の選択
        if np.random.uniform(0, 1) < epsilon:
            next_action = env.action_space.sample()
        else:
            next_action = np.argmax(Q[next_observation, :])

        # Q値の更新
        Q[observation, action] += alpha * (reward + gamma * Q[next_observation, next_action] - Q[observation, action])

        # 状態と行動の更新
        observation = next_observation
        action = next_action

        # エピソードの終了判定
        if done:
            break

        # ステップ数のカウント
        t += 1

    # 1エピソードの結果の出力
    print("Episode {}: {} steps".format(i+1, t+1))

# 環境のクローズ
env.close()

while文の中でQ値が更新されています。

Q学習

Q学習は方策オフ型の手法で、現在の状態で取った行動に対する最大のQ値を使用してQ関数を更新します

import gym
import numpy as np

# Qテーブルの初期化
Q = np.zeros((4, 2))

# ハイパーパラメータの設定
alpha = 0.1  # 学習率
gamma = 0.9  # 割引率
epsilon = 0.1  # ε-greedy法のε

# 環境の作成
env = gym.make('CartPole-v0')

# エピソード数
num_episodes = 1000

# 各エピソードの処理
for i in range(num_episodes):
    # 環境の初期化
    observation = env.reset()

    # ステップ数のカウント
    t = 0

    # 1エピソードの処理
    while True:
        # 初期状態での行動の選択
        if np.random.uniform(0, 1) < epsilon:
            action = env.action_space.sample()
        else:
            action = np.argmax(Q[observation, :])

        # 行動の実行
        next_observation, reward, done, info = env.step(action)

        # Q値の更新
        Q[observation, action] += alpha * (reward + gamma * np.max(Q[next_observation, :]) - Q[observation, action])

        # 状態の更新
        observation = next_observation

        # エピソードの終了判定
        if done:
            break

        # ステップ数のカウント
        t += 1

    # 1エピソードの結果の出力
    print("Episode {}: {} steps".format(i+1, t+1))

# 環境のクローズ
env.close()

SARSAとQ学習の違い

SARSA: 現在の状態(S)、選択した行動(A)、得られた報酬(R)、次の状態(S')、そして次の行動(A')を元にQ値を更新する。

# Q値の更新
Q[observation, action] += alpha * (reward + gamma * Q[next_observation, next_action] - Q[observation, action])

Q学習: 最大のQ値を持つ行動を元にQ値を更新する。

# Q値の更新
Q[observation, action] += alpha * (reward + gamma * np.max(Q[next_observation, :]) - Q[observation, action])