ChainerとCuPyによるチューリングパターン

[『作って動かすALife 実装を通した人工生命モデル理論入門』　岡 瑞起、池上 高志、ドミニク・チェン、青木 竜太、丸山 典宏　著] (https://www.oreilly.co.jp/books/9784873118475/)

[GitHubのサポートサイト] (https://github.com/alifelab/alife_book_src) (MITライセンス)

この書籍の2章ではチューリングパターンが取り上げられており、サポートサイトにはサンプルコードが用意されています。
[gray_scott.py] (https://github.com/alifelab/alife_book_src/blob/master/chap02/gray_scott.py)
この境界条件のシンプルなコードを参考にして、Numpy + SciPy 版とChainer + CuPy 版をつくり、実行速度の比較をしました。
サンプルコードではnp.roll()でラプラシアンの計算をしていますが、これを単純にcp.roll()に置き換えただけではむしろ遅くなってしまいます。機械学習ライブラリの畳み込みを利用して、ラプラシアンフィルタによる演算に置き換えれば、GPUによる高速化を簡単に実現できます。

NumPy + SciPy 版

import numpy as np
from scipy import ndimage
import time
import matplotlib.pyplot as plt

step = 10000      # 計算ステップ
grid = 128      # グリッドサイズ
square = round(grid//6, -1)     # 初期配置のサイズ
dx = 0.01       # グリットの空間差分 
dt = 1.0        # ステップの離散時間
Du = 2.0e-5       # 拡散係数
Dv = 1.0e-5
f, k = 0.035, 0.065     # feed率とkill率  
#f, k = 0.040, 0.060   # amorphous
#f, k = 0.012, 0.050   # wandering bubbles
#f, k = 0.025, 0.050   # waves
#f, k = 0.022, 0.051   # stripe

# 初期の濃度分布
u = np.ones((grid, grid), dtype=np.float32)
v = np.zeros((grid, grid), dtype=np.float32)
u[grid//2-square//2:grid//2+square//2, grid//2-square//2:grid//2+square//2] = 0.5
v[grid//2-square//2:grid//2+square//2, grid//2-square//2:grid//2+square//2] = 0.25

# 対称性を崩すためのノイズ
np.random.seed(seed=0)
u += np.random.rand(grid, grid)*0.1
v += np.random.rand(grid, grid)*0.1

# ラブラシアンフィルタ
w = np.array([[0,1,0], [1,-4,1], [0,1,0]], dtype=np.float32)

Du_dxdx = Du / (dx*dx) # Du / dx^2の事前計算
Dv_dxdx = Dv / (dx*dx) # Dv / dx^2の事前計算

time_start = time.clock()

for i in range(step):
    # NumPyでラプラシアンを計算する場合
    #Lu = (np.roll(u, 1, axis=0) + np.roll(u, -1, axis=0) + np.roll(u, 1, axis=1) + np.roll(u, -1, axis=1) - 4*u)
    #Lv = (np.roll(v, 1, axis=0) + np.roll(v, -1, axis=0) + np.roll(v, 1, axis=1) + np.roll(v, -1, axis=1) - 4*v)
    
    # SciPyでラプラシアンを計算する場合
    # ここでは境界条件を定数(cval)0のパディングにしています。
    # mode='warp'にするとnp.rollと同じ境界条件になります。
    Lu = ndimage.convolve(u, w, mode='constant', cval=0.0)
    Lv = ndimage.convolve(v, w, mode='constant', cval=0.0)
    
    # Gray-Scottモデルの反応拡散方程式
    dudt = Du_dxdx * Lu - (u * v * v) + f * (1.0 - u)
    dvdt = Dv_dxdx * Lv + (u * v * v) - (f + k) * v
    u = u + dt * dudt
    v = v + dt * dvdt

time_numpy = time.clock() - time_start
print(time_numpy, "s")
plt.imshow(u)
plt.show()

# このコードは下記URLを参考にして作りました。
# https://github.com/alifelab/alife_book_src/blob/master/chap02/gray_scott.py

Chainer & CuPy版

import numpy as np
import cupy as cp
import chainer
import chainer.functions as F
import time
import matplotlib.pyplot as plt

step = 10000       # 計算ステップ
grid = 128      # グリッドサイズ
square = round(grid//6, -1)     # 初期配置のサイズ
dx = 0.01       # グリットの空間差分
dt = 1.0        # ステップの離散時間
Du = 2.0e-5       # 拡散係数
Dv = 1.0e-5
f, k = 0.035, 0.065     # feed率とkill率  
# f, k = 0.040, 0.060   # amorphous
# f, k = 0.012, 0.050   # wandering bubbles
# f, k = 0.025, 0.050   # waves
# f, k = 0.022, 0.051   # stripe

# 初期の濃度分布
u = cp.ones((grid, grid), dtype=np.float32)
v = cp.zeros((grid, grid), dtype=np.float32)
u[grid//2-square//2:grid//2+square//2, grid//2-square//2:grid//2+square//2] = 0.5
v[grid//2-square//2:grid//2+square//2, grid//2-square//2:grid//2+square//2] = 0.25

# 対称性を崩すためのノイズ
cp.random.seed(seed=0)
u += cp.random.rand(grid, grid)*0.1
v += cp.random.rand(grid, grid)*0.1

#ラプラシアンフィルタ
w = cp.array([[0,1,0], [1,-4,1], [0,1,0]], dtype=np.float32)

#Chainerで計算するために、(N, CH, H, W)の形式に整える
u = u[cp.newaxis, cp.newaxis, :, :]
v = v[cp.newaxis, cp.newaxis, :, :]
w = w[cp.newaxis, cp.newaxis, :, :]

Du_dxdx = Du / (dx * dx) # Du / dx^2の事前計算
Dv_dxdx = Dv / (dx * dx) # Dv / dx^2の事前計算

#CuPyのElementwiseKernelによるGray-Scottモデルの反応拡散方程式
cupy_dudt_dvdt = cp.ElementwiseKernel(   
    'T Du_dxdx, T Dv_dxdx, T Lu, T Lv, T u, T v, T f, T k, T dt',
    'T z1, T z2',
    'z1 = ((Du_dxdx * Lu) - (u * v * v) + (f * (1.0 - u))) * dt + u , z2 = ((Dv_dxdx * Lv) + (u * v * v) - (( f + k ) * v)) * dt + v',
    'cupy_dudt_dvdt'
)

time_start = time.clock()

for i in range(step):
    # chainer.functions.padで境界条件を設定する場合
    # np.rollと同じ境界条件にするmode='warp'には対応していません。
    #up = F.pad(u, ((0,0),(0,0),(1,1),(1,1)), mode='reflect')
    #vp = F.pad(v, ((0,0),(0,0),(1,1),(1,1)), mode='reflect')
    #Lu = F.convolution_2d(up, w, stride=1, pad=0).data
    #Lv = F.convolution_2d(vp, w, stride=1, pad=0).data
    
    # chaienr.functions.conbolution_2dのpaddingで境界条件を設定する場合
    # この場合、定数0のpaddingになります。
    # F.のfunctionsクラスにndarrayを代入するとVariableクラスで返るため、
    # 末尾に.dataを付けてndarrayに戻します。
    Lu = F.convolution_2d(u, w, stride=1, pad=1).data
    Lv = F.convolution_2d(v, w, stride=1, pad=1).data
    
    # Gray-Scottモデルの反応拡散方程式
    u, v = cupy_dudt_dvdt(Du_dxdx, Dv_dxdx, Lu, Lv, u, v, f, k, dt)

time_cupy = time.clock() - time_start
print(time_cupy, "s")
plt.imshow(cp.asnumpy(u[0,0,:,:]))
plt.show()

# このコードは下記URLを参考にして作りました。
# https://github.com/alifelab/alife_book_src/blob/master/chap02/gray_scott.py

## 計算結果の相違 NumPy版とCuPy版で、 `np.random.seed(seed=0)` `cp.random.seed(seed=0)` とシード値を揃えてみましたが計算結果は異なりました。 NumPyとCuPyでは同じシード値でも出てくる乱数は異なるようです。 他にSciPyとChainerで計算精度が違う等の要因もあるかもしれません。  step = 10000, grid = 128 ***  step = 10000, grid = 256 ***  step = 10000, grid = 512 ***

計算時間の比較

小さい配列で長く回すと並列の効果は薄いですが、配列が大きくなるほど恩恵が大きくなりました。
step = 10000



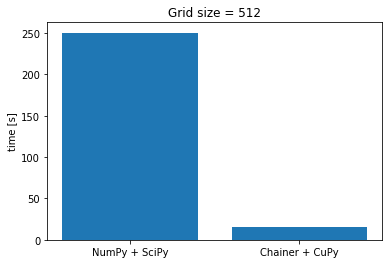
動作環境

• Windows 10
• CPU: Intel Core i7 6700HQ 2.60GHz
• GPU: NVIDIA GeForce GTX 960M
• Python 3.6.5
• NumPy 1.17.0 + MKL
• SciPy 1.3.0
• Chainer 6.2.0
• CuPy 6.2.0
• CUDA 8.0.60

まとめ

• ラプラシアンの計算を、書籍サンプルコードのnp.roll()からラプラシアンフィルタの畳み込みにしました。
• 畳み込み演算にChainerのchianer.functions.convolution_2d()を用いたことで、CuPyのUser-Defined Kernelsよりも簡潔に実装できました。
• chainer.functions.pad()、cupy.pad()は、numpy.pad()の全てのmodeに対応しておらず、かつ遅いため、様々な境界条件を速く走らせるには、CuPyのユーザー定義カーネルで実装する必要があるとわかりました。