タイタニック・チュートリアル 欠損値をどうするか 1

欠損値への対処

Kaggleのタイタニック・チュートリアルのデータを使って欠損値への対処方法を学んでいきます。

欠損値とは

欠損値の他に、欠測値や欠落値という呼び方もあるようです(もう「欠.?値」という正規表現でいいんじゃないか)。英語だとmissing value。要するにデータセット内の空白です。測定ミスなのか入力ミスなのか理由はいろいろ。

※この文書中は欠損値で統一します。

欠損値に困る

僕のような実務データに触れた事の無いデータ分析初心者が、Kaggleの導入としてタイタニック号の生存予測をやろうとすると、欠損値の対処に困るのではないかと思います。僕は今まさに困っています。

何故困るかというと、機械学習・データ分析・統計の初級者向けの本には欠損値をどうすべきか、なんて事はこれっぽっちも書いていないから。

他方でちょっと欠損値について調べてみると、欠損値は扱い方次第でモデルの予測性能に結構な影響を与えるっぽい事が伺い知れます。欠損値に対する戦略が必要そうです。

タイタニックのデータセットの欠損を確かめる

titanic.py

import pandas as pd

## トレーニングデータとテストデータのCSVファイルをpandasデータフレームとして読み込み
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')

## 概要確認
train.head(3)
test.head(3)

## トレーニング、テストデータのデータ数確認
len(train.index)
# 891
len(test.index)
# 418

## 値がnullの項目数を数える
train.isnull().sum()
# PassengerId      0
# Survived         0
# Pclass           0
# Name             0
# Sex              0
# Age            177
# SibSp            0
# Parch            0
# Ticket           0
# Fare             0
# Cabin          687
# Embarked         2

test.isnull().sum()
# PassengerId      0
# Pclass           0
# Name             0
# Sex              0
# Age             86
# SibSp            0
# Parch            0
# Ticket           0
# Fare             1
# Cabin          327
# Embarked         0

AgeとCabinは欠損が多い事が分かります。特にCabinは半分以上が欠損値です。

原因の違いによる3種類の欠損値

単に欠損値と言っても、欠損の原因によって3種類あります。原因によって対処方法も異なるので、どんな種類があるか抑える必用があります。

まず以下の用語について意味を抑えて下さい。

観測値: 実際に観測できたデータ(既知)
欠損値: 観測できなかったデータ(未知)
完全データセット: 欠損値の無いデータの集合
不完全データセット: 欠損値が存在するデータの集合

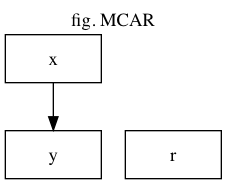
MCAR (Missing Completely At Random)

完全にランダムな原因で欠損が発生した場合です。例えばデータの入力漏れとかはこれに当たるでしょう。

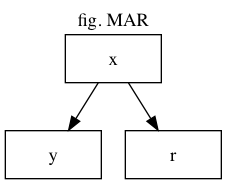
MAR (Missing At Random)

観測値に応じて欠損した値です。良くある例ですが、性別、年齢、体重、身長といったデータを測定した時、体重の値に幾つか欠損値があったとしましょう。この体重の欠損が、若い女性の場合に多いとするならば、この欠損は体重と年齢に応じて発生している、というわけです。

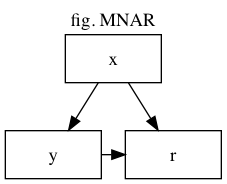
MNAR (Missing Not At Random)

欠損値自体に応じて欠損した値です。先程の体重の例で言うならば、体重が重い場合に欠損が多く発生する、といった時です。(不思議なんだけど欠損しているデータが、それ自身が原因で欠損したかどうか、なんてどうやって知るのでしょうね)

それぞれの欠損メカニズムを有向グラフで理解する

MCAR、MAR、MNARの3種類の欠損メカニズムを、有効グラフで表現していみましょう。

それぞれの変数の意味は

x : 独立変数、欠損無し
y : 目的変数、欠損有り
r : yに欠損がある時1、無い時に0になるような確率変数

グラフ中の矢印は、矢印の元が矢印の先に影響を与えている事を示します。例えば「x→y」ならば、xが変化するとyも変化するという事です。

対処法の概要

では対処方法を個別に見ておきましょう。それぞれの手法は適用できる欠損メカニズムに違いがあります。

リストワイズ削除

欠損値があった場合、単にそのデータを削除して残りのデータを使って推測する方法です。例えば以下のデータを考えましょう。ジェームズ・キャメロンの身長の値が欠損しています。

名前	年齢	性別	身長
レオナルド・ディカプリオ	22	男	181
ケイト・ウィンスレット	21	女	169
ジェームズ・キャメロン	42	男	欠損	欠損があるのでこの行ごと削除
セリーヌ・ディオン	29	女	171

この場合、ジェームズ・キャメロンのデータは一切使わず残り3人分のデータを使いなんらかの推定を行なうというのがリストワイズ処理です。

リストワイズ処理は欠損原因がMCARの時は上手く作用する事が知られています。使用する標本数が小さくなるので推定自体は悪化しますが、標本数に対して欠損数が充分少なければ問題にはなりません。

単一代入法

代入モデルと呼ばれる欠損値を予測する何らかのモデルを作り、まずそのモデルによって作られた値で欠損値を埋めます。そうして欠損値を無くした擬似的完全データセットを1つ作成し、そのデータセットを用いて推定を行なう手法です。主な代入モデルには以下のものがあります。

• 回帰代入法
• 比率代入法
• 平均値代入法
• コールドデック法
• ホットデック法
• 完全情報最尤推定法

誤差項を考慮するか否かにより、確定的代入法と確率的代入法に分類できます。

MARによる欠損であれば単一代入法で概ね上手く行きます。しかし単一代入法では一般にデータの分散を過小評価しがちになります。例えば回帰代入であれば、モデルから予測して補完された欠損値は全て回帰直線上にプロットされてしまいます。つまり欠損値の分散はゼロです。これに対処するのが次の手法です。

多重代入法

代入モデルから欠損値を埋める値を予測するのは単一代入法と同じです。多重代入法では欠損値を埋めた疑似的完全データセットを複数作ります。そしてそれぞれの擬似的完全データセットを用いて別個に推定を行ない、複数の推定結果を統合して最終的な推定結果とするのがこの方法です。

多重代入法を用いる事でデータの持つ不確定性や分散を適切に評価できると考えられます。主なものとして以下の手法があります。

• DA(Data Augumentation)アルゴリズム
• FCS(Fully Conditional Specification)アルゴリズム
• EMB(Expectation-Maximization with Boot-strapping)アルゴリズム

ここまでの説明を見るとMNARに対応した手法が無いことが分かると思います。一般的にMNARの欠損に対処するのは難しいのですが、分析モデルに充分に統制された補助変数を加える事で、MNARをMARに変える事ができれば、MARとして分析可能になります。

機械学習的手法

機械学習のk-近傍法やランダムフォレストを使って欠損値を埋めるという手法もあります。この場合、欠損値を目的変数として、それ以外の特徴量を独立変数としてモデルを構築する事になります。

タイタニック・データセットで言えば、Ageを目的変数にし、それ以外の特徴量を独立変数とするわけです。ただしテスト・データに値が含まれていないSurvivedのデータは使えません。Ageが欠損していないデータをトレーニング・データにして、欠損している方をテスト・データとすれば教師あり学習が可能です。

その2に続きます。

参考サイト

• 欠損値の対処法
• 欠損値があるデータの分析
• 完全情報最尤推定法による欠損値補完
• 機械学習のための欠損値処理まとめ
• EMアルゴリズム徹底解説
• 欠損データ分析 (missing data analysis)
  , pdf
• 剰余変数を統制するのは大事だよ、という話
• How to Handle Missing Data with Python
• iskandr/fancyimpute, github
• 様々な多重代入法アルゴリズムの比較, pdf
• テキストデータをグラフ画像に変換するツール「Graphviz」ことはじめ
• Graphvizとdot言語でグラフを描く方法のまとめ

参考書籍

• 欠測データ処理 Rによる単一代入法と多重代入法