confusion_matrix関数で出力できるのは混同行列です。
教師あり学習の分類は、正解率だけでは評価できない場合があります。
例えば「0, 1, 2, 3, 4, 5, 6, 7, 8, 9」の数字の画像から「9以外」を予測する場合、単純に「すべて9以外と予測する」だけで正解率は90%になります。
このようなケースでは、metricsモジュールのconfusion_matrix関数で混同行列を出力すると、データやモデルの偏りが分かります。
上の例をconfusion_matrix関数にかけると、次の件数が出力されます。
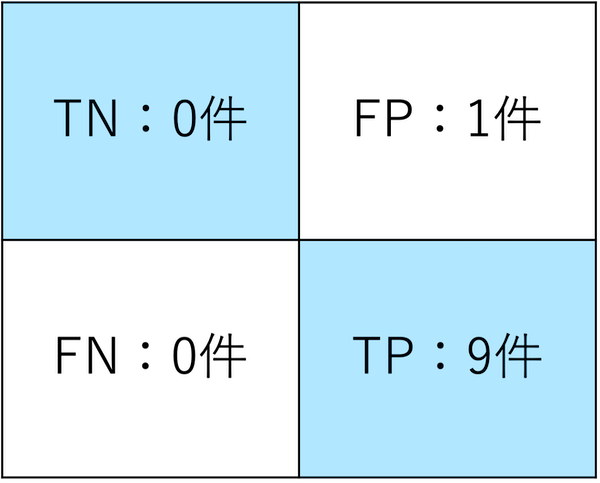
対角線にある青色のTNとTPが正確に分類された個数です。アルファベットは次の意味になります。
T → True → 正解
F → False → 不正解
P → Positive → 正例(9以外)
N → Negative → 負例(9)
TN → 9と予測して9以外
FN → 9と予測して9
FP → 9以外と予測して9
TP → 9以外と予測して9以外
正解率は90%ですが、負例の「9」と予測するTNとFNの件数が0です。また、合計10件に対して「9以外と予測して9以外」となったTPが9件もあるので、偏りがあるといえます。
このように混同行列はデータやモデルの偏りが分かります。ただし、極端な例であれば混同行列でも判断できますが、出力された件数だけでは判断できない場合があります。そこで、定量的に判断できる「適合率、再現率、 F値、正解率」を確認します。
「適合率、再現率、 F値、正解率」は、metricsモジュールのclassification_report関数で出力します。