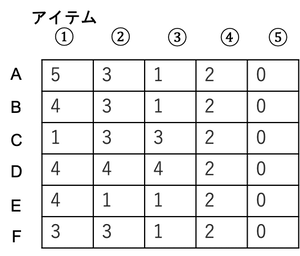仕事で推薦システムについて勉強したので、まとめます。
内容は以下の通りです。
- Factorization machine 周辺技術の変遷
- Factorization machineについて
- Factorization machine を用いて映画評価の予測をしてみる (未完)
Factorization machine 周辺技術の変遷
協調フィルタリング
ここでは、協調フィルタリングの中でもユーザーベースの手法について述べます。
ユーザーの類似度をコサイン類似度やピアソンの相関係数などを用いて算出し、類似度の高いユーザーと同じような商品を推薦する手法です。
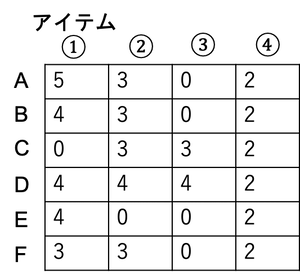
以下の評価値行列を考えます。評価値行列とは、各ユーザーの各アイテムに対する評価値からなる行列です。(未購入アイテムの評価値の埋め方は色々存在するようですが、今回は簡単のため0で埋めています。)
この行列の類似度をピアソンの相関係数を用いて計算します。そうするとユーザーBともっとも類似度が高いのはユーザーAであると判断できます(計算するまでもないですが)。
そして、この計算結果をどう使うのかというと
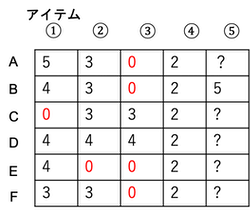
例えば、この評価値行列の中に入っていないアイテム5を考えます。このアイテム5に対するユーザーBの評価値が5である場合、ユーザーAに対してもこの商品をレコメンドしてやれば(類似度が高いことから)高評価になるはずので、購入してくれるだろうとなるわけです。
良さそうですね。しかしここで注目して欲しいのが、評価値行列の「0」の部分です。
0は未購入(未評価)を意味していますが、それを0として数値の情報に置き換えてしまうと、0~5の6段階評価をしているという意味になりかねません。(というよりなってます。)
要するに
- 1~5は正当なアイテムの評価で0はアイテム未購入
という意味が
- 0~5でアイテム評価
という意味に変わってしまいます。
これでは元データを正確に反映させた計算ができているとは言い難いですね。最終的には「類似度が高いユーザー」かつ「評価値が高いアイテム」をレコメンドするので、全ユーザーがまだ未評価のアイテム(要素が全て0のカラム)をレコメンドすることもできません。
そこでこの問題を解決するために生まれたのが、次に説明するMatrix Factorizationです。
Matrix Factorization
日本語だと行列因子分解です。Factorizationの有名な手法の一つに特異値分解(SVD)があります。この手法は、ユーザーの特徴量をユーザーデータ、重み、カテゴリーの3つの行列に分解するイメージです。
SVDは解析的に行列分解していますが、Matrix Factorization(少なくともこの論文)では、勾配降下法を用いて近似的に行列分解をしています。
損失関数
簡単にロスの導出について説明します。
まず、以下のように行列が分解できると仮定します。
これが一般化線形モデルで言う所の仮定関数に相当します。この行列の計算結果が学習データである評価値行列に近くなるように学習していきます。
学習データである評価値行列をR, 分解後のPの行ベクトルを$p$、Qの列ベクトルを$q$とします。
評価値行列Rの各要素$r$と$p\cdot q$ の計算結果が等しくなれば良いので、
$r- p \cdot q = 0$ になって欲しいわけです。最適化するときは、
$r- p \cdot q$ の2乗を全要素に対してsumしてやれば、損失関数の出来上がりです。要するに最小2乗誤差ですね。
以下に論文で示されている損失関数を示します。
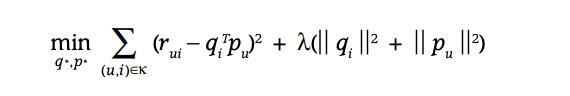
式中の$q_i$と$p_u$はユーザー情報が格納されている行列Pの行ベクトル、アイテム情報が格納されている行列Qの列ベクトルに相当し、$q_ip_u$は各ユーザーの各アイテムに対する評価を計算していることになります。
後ろの第2項はよく見るL2正則化ですね。
線形回帰やロジスティック回帰におけるL2正則化項は、
$\frac{\lambda}{2} \sum_i^n |{w_i}|^2$
と表されるので重みベクトルのノルムの2乗を足していたことを考えると、これも過学習防止のための正則化項として考えて良さそうです。
最適化する$p_u$と$q_i$の更新式は、
損失関数を$p_u$と$q_i$についてそれぞれ偏微分したものが勾配となるので以下のようになります。
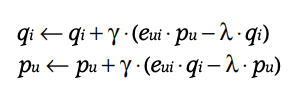
この手法のきも
で、なぜこの手法がアイテム評価予測において協調フィルタリングより優れているのかについて説明します。
今度は全員未評価のアイテム5を含んだ評価値行列を考えます。
MFを用いる場合においても未評価アイテムについて予測値との誤差を計算するため、どちらにしろ何かの値で埋める必要があります。ここでは、例として未評価アイテムを「0」とします。
先ほどの更新式を用いて近似的に行列分解してやると$p_u$と$q_i$が求まります。そしてこの$p_u$と$q_i$を用いて、Rの各要素を計算してやれば、各ユーザーの各アイテムの予測評価値が算出されます。
# 行がユーザー、列がアイテム
array([[4.99674813, 2.78373313, 1.09673171, 2.22729147, 1.08047493],
[4.14907991, 2.63034434, 1.30414767, 1.97952826, 0.90497689],
[1.18804491, 3.01313265, 3.16224341, 1.48881473, 0.31440093],
[3.67874171, 4.2920269 , 3.57479319, 2.55469387, 0.85032001],
[3.83623452, 1.83493529, 0.46901327, 1.58667925, 0.82213824],
[3.30013542, 2.47617897, 1.51120262, 1.73116941, 0.72920128]])
やはり未評価のアイテム5の評価を「0」としてるので、予測評価も比較的「0」に近い値になります(元の評価値行列Rに近づくようにSGDで最適化するため)。
ここで、**「0で埋めて、それに近づくようにSGDで最適化するなら、単純に0埋めしてるだけの協調フィルタリングと同じでは?」**という疑問が生じると思います。
しかしこの手法の用途は、協調フィルタリングでは不可能だった**「未評価(未購入)アイテムをレコメンドすること」**であり、未評価アイテムに対するユーザー間の相対的な評価がわかれば良いわけです。
つまり、未評価アイテム5をどのユーザーに対してレコメンドするかという視点で考えた場合、重要なのはユーザー間の相対的な評価であり、0付近であるという絶対的な大きさには意味がありません。
まとめると、「最初は0で埋めるけど、最適化すると実は0は全部0として同じではなく、ちゃんと大小あるんだよ」ということを表現するために、Matrix Factorization(以下MF)が生まれたわけです。
Factorization Machine
これまでの評価値行列の例では「誰がどのアイテムを購入したのか」という情報のみでしたが、
- 過去に何回サービスを利用しているか(例:amazonなら何回ポチっているか)
- いつ購入したのか
- 値段はいくらか
などの情報も考慮して評価を予測したいところです。MFではそういった評価値以外の情報を考慮することができませんが、Factorization Machine(以下FM)ではそれらを任意に特徴量として加えることができるというメリットがあります。
上記の点以外にも、MFとFMではデータの作成方法が大きく違います。
MFでは、ユーザー情報は全て同一行に収められていましたが、FMの場合ユーザーごと、アイテムごとでone-hotエンコーディングした状態でデータを用意します。
実サービスでは、ユーザー数やアイテム数(ユーザーが購入した商品など)はとても多いので、one-hotエンコーディングするとスパース行列になります。つまり同じユーザーでも見ている映画が異なれば違うレコードとして複製されるようなものなので、直感的には丁寧な扱い方な気がします。
FMの予測式
評価値以外の情報を予測に反映させるために、特徴量同士の交互作用項を取り入れているのがこの手法のミソです。リッジ回帰の予測式によく似ていますね。
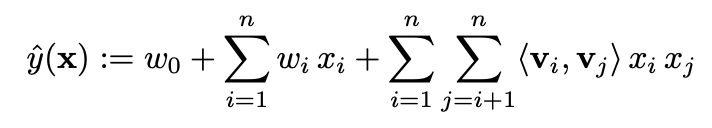
上式の右辺第三項が特徴量の交互作用項を意味しています。
ここで、この項が何を意味しているのかを考えてみます。k=2(kはハイパーパラメーター)における重みベクトル$V_i$、$V_j$の成す角度を$\theta_{ij}$とおくと、この内積の計算は
$V_i \cdot V_j = V_i \cdot V_i \cos\theta_{ij} = |V_i|^2 \cos\theta_{ij}$
となります。これはリッジ回帰におけるL2正則化項を2つの特徴量のなす角度(2つの特徴量の異なり度合い)で重みづけした項と考えることができます。仮に正則化項の中に2つの特徴量の違いを反映させることが目的ならば、単純に$\cos \theta_{ij}$だけでも良い気がしますし、$x_ix_j$がなくても、交互作用の役割は果たせる気がします。
この辺りの予測式をいじって検証したらそれはそれで面白そうです。
SVMとの比較
以下に多項式SVMにおける予測式を示します。
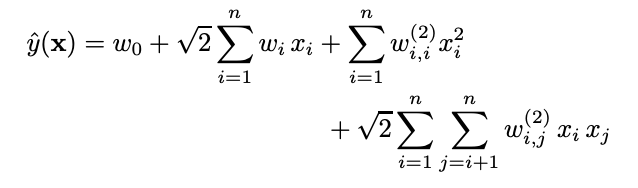
論文の通り、あるユーザーu、あるアイテムiの特徴量にフラグが立っているとすると、上の式は、

となります。右辺第3項と第4項は$w_u$$w_i$と同義ですので(論文参照)、
$\hat y(x) = w_0 +(\sqrt2 + 1)(w_u + w_i)+\sqrt2 w_{u,i}^{(2)}$
となります。右辺の最終項である$w_{u,i}^{(2)}$ はユーザーuかつアイテムiにフラグが立っているデータが入力された場合のみ計算がされます。そうすると、そのようなデータは学習中1回しか登場しないので、更新が行われなく正確に最適化されないと主張しています。それが論文中で述べられている「SVMのスパースデータに対する脆弱性」だと思われます。
ではFMの場合はどうでしょうか。
同様にあるユーザーu、あるアイテムiの特徴量にフラグが立っている場合の評価値をFMの予測式を用いて計算すると、以下のようになります。
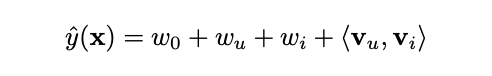
$V_u$と$V_i$は他の特徴量との相互作用を考える時もこれらの重み($V_u$と$V_i$はベクトルであることに注意)は共有されるので、更新されやすくなります。
以下の式を見てください。あるユーザ-jのあるアイテムiの評価値の予測式です。
$\hat y(x) = w_0 + w_j + w_i + \langle{V_j} , {V_i} \rangle$
右辺第四項(交互作用項)に注目すると先ほど登場した、${V_i}$が出現しています。すなわち、**特徴量の交互作用項の重み$V_{x}$(xは任意の特徴量)は各特徴量ごとに固定であり、その重みを共有することでスパースなデータに対しても更新させる回数を多くしています。
ここで注意しなければいけないのは、同じ特徴量xに関する重みでも交互作用項に対する重み$V_x$と特徴量xに対する$w_x$は別ものだということです。
FMはこの重み共有というアイデアにより、計算時間を短縮し、SVMでは弱かったスパースなデータに対しても適用可能になっています。計算時間に関しては、$O(kn)$で済むそうです。導出の詳細は論文に載っています。
また本論文では、SVMとの比較だけでなく他の行列因子分解を用いた手法との比較も述べられていました。
Factorization machine を用いて映画評価の予測をしてみる
重要そうなハイパーパラメーターについても勉強したかったので、fastFM[https://github.com/ibayer/fastFM] を用いてモデルを動かしてみました。
https://www.kaggle.com/netflix-inc/netflix-prize-data ←こちらのデータの一部を用いて予測をしてみます。
結果をまとめ次第投稿します。
参考文献