21日のアドベントカレンダーを2日遅れでお届けしております。
忘年会シーズンに入る前に調べておけばよかったと反省するばかり。二日酔いが辛い…。
気を取り直して、今回はFactorization Machines(以下、FM)について書いていきます。
1ヶ月ほど前にRecSys2014読み会で知ってから結構気になっていたで、調べてみた結果をまとめています。
FMはRendleさんが2010年にICDMに出したのが初出の様なので、割りと前から存在していたのですが、完全にノーマークでした。研究はRendleさんがほぼメインで行っている様ですが、KDD2014のNetflixが出しているまとめにも載っているので、業界的には結構有名なんだろうと思います。ノーマークだったけどorz
はじめに
協調フィルタ系のレコメンドにトレンドについては、
Collaborative Filtering(CF)
→ SVD / Matrix Factorization(MF)
→ SVD++
→ time-SVD / Pairwise Interaction Tensor Factorization(PITF) / Factorizing Personalized Markov Chains(FPMC)
という流れかなと個人的には思っていますが、time-SVDあたりからはUser-ItemのRating以外の要素を取り込む様な拡張になっています。
こういった派生系はだいたい特定のケースに特化したモデルがちらほら生まれてきて、特化したケースを一般化した汎化モデルが出てくるパターンだと思います。
FMはこの汎化モデルにあたる位置付けです。
Factorization Machinesとは?
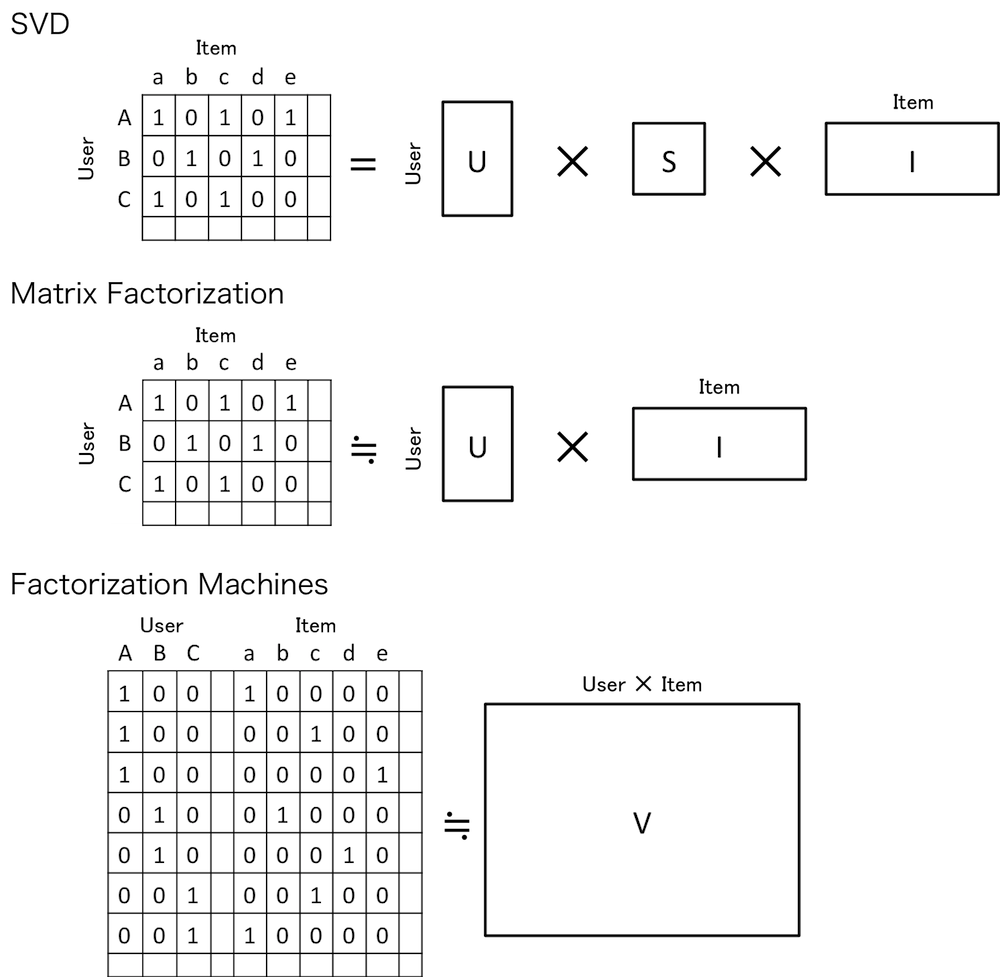
とりあえず、SVD/MF/FMの違いをイメージで書いてみました。
FMはSVDやMFとはRatingの持ち方が異なっています。
SVDやMFは1行に1ユーザの評価データを複数格納しており、これをユーザとアイテムの特徴ベクトルをそれぞれ取り出しています。
これに対して、FMは1評価を1行で表し、取り出すのはユーザとアイテムの交互作用(pair-wise)の特徴ベクトルで、SVDやMFとは注目している対象が異なります。
FMの予測式は以下の様になります。
\hat{y}(\mathbf{x}):= w_0 + \sum_{i=i}^nw_ix_i + \sum_{i=1}^n\sum_{j=i+1}^n<\mathbf{v}_i ,\mathbf{v}_j>x_ix_j
$\mathbf{x}$は上の図のFMの図の1行に該当するので、ユーザとアイテムの両方に1が立つ感じですね。
Netflixの資料には$f(\mathbf{x})=b+w_u+w_i+\mathbf{v}^T_u\mathbf{v}_i$と書いてあるので、こちらの方がMFを知ってる人には分かりやすいかも。
$\mathbf{w}\mathbf{x}=w_u+w_i$と思ってもらえれば上の式との対応は伝わるかな。
なので、FMではユーザバイアス$w_u$、アイテムバイアス$w_i$に加えて、ユーザとアイテムの交互作用$\mathbf{v}^T_u\mathbf{v}_i$を使って予測をっているということになります。
どの辺りが汎化モデルなのか?
この相互作用を時間とかContextとかを自由に入れられます。
引用元:http://www.slideshare.net/xamat/kdd-2014-tutorial-the-recommender-problem-revisited
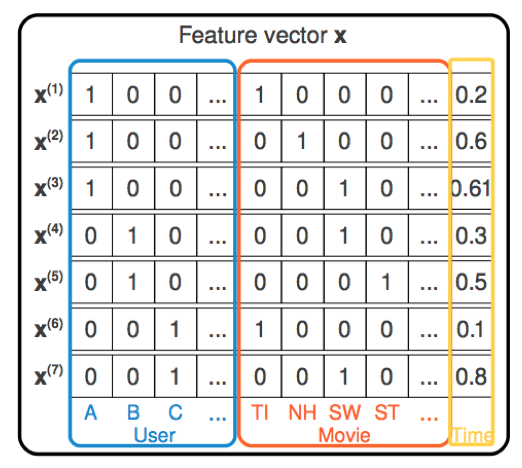
上記の例では、UserとItem以外にTimeという閲覧タイミングを入れています。
こうすることで、User✕Item✕Timeの交互作用をモデルで扱うことができます。
Rendleさんの元論文では以下の様な例を挙げており、UserとItem以外を自由に入れられる、且つ幾つでも入れることができるそうです。
なので、時間だけでなく、場所や気分といったContextを入れることも可能です。
引用元:http://www.ismll.uni-hildesheim.de/pub/pdfs/Rendle2010FM.pdf
推定方法
以下の手法で推定が可能です。
- SGD
- Adaptive SGD
- ALS
- MCMC
推定時はL2正則化を掛けて行います。
性能
Matrix Factorizationよりはやっぱりいいらしい。
KDD Cup2012のCTR予測ではRendleさん1人で挑んで2位だったとのこと。
どうやったら使えるのか?
Rendleさんお手製のlibFMというライブラリがあるので、それを使うのがおそらくベストの様です。
FMはMatrixの持ち方も変わっており、普通にRatingの行列を作ると凄い量になってしまいますが、libFMの中ではRating行列の共通部分を集約して持つようにしたりしていて、メモリ量の削減にもかなり力を入れてあります。
現状使うのであれば、libFMを使うか、libFMベースで手を入れるのが良さそうです。
実行サンプル
1回試して力尽きました。
そのうち他手法との比較結果を挙げようと思います。