畳み込みニューラルネットの規模と正答率の実験

以下の記事は自身がやってるブログを日本語化したもの

ブログ

概略

畳み込み式ニューラルネットワークはレイヤーの数やレイヤーあたりのノード数でどのように識別精度が変動するのかがわかりにくい。個人的には全くわからない。深く大きくすれば上がるなー程度の認識しかない。
そこで、cifar-10を用いて、ネットワークの変化に応じた精度変化を少しだけ見てみる。使用環境がMacbook proなので大規模ネットワークや様々なタイプのネットワークの変化を追っていくのは厳しいため、かなり限定的に見ていく。

使用データ

今回使用するのは、フリーのカラー画像データセットであるcifar-10。
名前の通り、10個のカテゴリを持っている。
作成していくモデルの目的はこの画像のカテゴリを予測することになる。

準備

ライブラリのインポートと画像データの準備。

import numpy as np
import keras
from keras.datasets import cifar10
from keras.models import Sequential
from keras.layers import Dense, Dropout, Conv2D, MaxPooling2D, Flatten, Activation
from keras.utils import to_categorical
from keras import backend as K

(x_train, y_train), (x_test, y_test) = cifar10.load_data()

これまで"cifar10.load_data()"を行ったことがなければダウンロードに少々時間がかかる。

モデル

畳み込み式ニューラルネットワークは作成者の判断で調整する箇所が非常に多い。

• 畳み込み層のレイヤーの数
• レイヤーあたりのノード数
• プーリング層の数と場所
• 行列を1次元化した後のレイヤー数
• ドロップアウトの仕込み箇所とその割合
• 正則化

そもそも、レイヤー数やノード数はいくらでも増やせるので、"あらゆるパターン"を試すのは不可能なので、今回はその大部分をテキトーに固定して実験する。

# make some type of model
def make_model_1(x_train, y_train, conv_num, dense_num):
    input_shape = x_train.shape[1:]


    # make teacher hot-encoded
    y_train = to_categorical(y_train, 10)

    # set model
    model = Sequential()
    model.add(Conv2D(conv_num, (3,3), activation='relu', input_shape=input_shape))
    model.add(MaxPooling2D(pool_size=(2,2)))
    model.add(Flatten())
    model.add(Dense(dense_num, activation='relu'))
    model.add(Dropout(0.4))
    model.add(Dense(10, activation='softmax'))
    model.compile(loss=keras.losses.categorical_crossentropy,
              optimizer=keras.optimizers.Adadelta(),
              metrics=['accuracy'])
    # training
    history =model.fit(x_train, y_train, batch_size=256, epochs=50, shuffle=True,  validation_split=0.1)
    return history

上記のモデルではまず、畳み込み層の持つノード数、一次元化後の層のノード数とそれぞれ、conv_num, dense_numとしてパラメーター化している。

実行

conv_num = [i for i in range(2, 12)]
dense_num = [pow(2, i+1) for i in range(8)]
outcome = []
for conv in conv_num:
    for dense in dense_num:
        history = make_model_1(x_train, y_train, conv, dense)
        outcome.append((conv, dense, history.history['val_acc']))

ループ処理の中でそれぞれのパラメーターでモデルを作成し、そのモデルのvalidation accuracyを確認できるようにしている。(後で思ったのはそもそも、オブジェクトごとリストに加えておけばよかった)

結果確認

import pandas as pd
import matplotlib.pyplot as plt

outcome_df = pd.DataFrame(outcome)
outcome_df.columns = ['conv_num', 'dense_num', 'accuracy']
plt.scatter(outcome_df['conv_num'], outcome_df['dense_num'], c=outcome_df['accuracy'], cmap='Blues') 
plt.colorbar()

結果は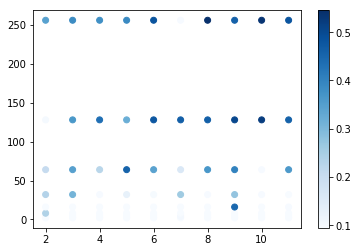
以上の図の通り。色の濃さが正答率を表している。とりあえず、二つのパラメーターの値が上がっていくと正答率が上がっていく傾向はあるっぽい。

さらに調査

現状だとたしかではないが、パラメーターの値の上昇に応じて正答率は上がっているようだ。conv_numとdense_numをそれぞれ10と256に固定して、畳み込み層と一次化後の層を増やしてみる。
また、さっきはvalidation accuracyしか見なかったので（出力形式の選択に後悔。。）、今回はtrain accuracyも観測してみる。

# add one more convolutional layer
def make_model_2(x_train, y_train, conv_num, dense_num):
    input_shape = x_train.shape[1:]


    # make teacher hot-encoded
    y_train = to_categorical(y_train, 10)

    # set model
    model = Sequential()
    model.add(Conv2D(conv_num, (3,3), activation='relu', input_shape=input_shape))
    model.add(Conv2D(conv_num, (3,3), activation='relu'))
    model.add(MaxPooling2D(pool_size=(2,2)))
    model.add(Flatten())
    model.add(Dense(dense_num, activation='relu'))
    model.add(Dropout(0.4))
    model.add(Dense(10, activation='softmax'))
    model.compile(loss=keras.losses.categorical_crossentropy,
              optimizer=keras.optimizers.Adadelta(),
              metrics=['accuracy'])
    # training
    history =model.fit(x_train, y_train, batch_size=256, epochs=50, shuffle=True,  validation_split=0.1)
    return history

history = make_model_2(x_train, y_train, 10, 256)

結果は以下の通り。

Epoch 50/50
45000/45000 [==============================] - 49s - loss: 0.3162 - acc: 0.8898 - val_loss: 1.9862 - val_acc: 0.5562

50エポック学習させて、train accuracyがだいたい0.9、validation accuracyがだいたい0.55。がっつり過学習してる。

この状態で実験を進めるのもよろしくないので過学習を解消する。

取る手段は以下の通り

• ドロップアウトをもっと多くの層に仕込む
• l1, l2, l1_l2などの正則化を利用する

ドロップアウトは学習時に一部のノードを不活性化させる手法、正則化は損失関数に対して項を新たに加えてパラメーターの値が大きくなるのを防ぐ手法となる。
とはいえ、なかなか面倒なのが、これらの手法をあらゆる層に仕込んだり、その値を強めすぎてしまうと、今度はtrain accuracyすらなかなか上がらなくなってしまう。
ここでは載せないが、実際、train accuracyがおよそ0.1から全く上がらないという状況になんども遭遇した。
常に過学習に気を配りながらモデルの精度を上げていけるようにネットワークを組んでいくのも大変なので、過学習を容認しながらaccuracyを上げていき(lossを減らしていき)、その後に過学習を解消した。

深めのモデル

def make_model_3(x_train, y_train, conv_num, dense_num):
    input_shape = x_train.shape[1:]

    # make teacher hot-encoded
    y_train = to_categorical(y_train, 10)

    # set model
    model = Sequential()
    model.add(Conv2D(conv_num, (3,3), activation='relu', input_shape=input_shape))
    model.add(Conv2D(conv_num, (3,3), activation='relu'))
    model.add(Dropout(0.2))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Conv2D(conv_num * 2, (3,3), activation='relu'))
    model.add(Conv2D(conv_num * 2, (3,3), activation='relu'))
    model.add(Dropout(0.2))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Flatten())
    model.add(Dense(dense_num, activation='relu'))
    model.add(Dropout(0.2))
    model.add(Dense(int(dense_num * 0.6), activation='relu'))
    model.add(Dense(10, activation='softmax'))
    model.compile(loss=keras.losses.categorical_crossentropy,
              optimizer=keras.optimizers.Adadelta(),
              metrics=['accuracy'])
    # training
    history =model.fit(x_train, y_train, batch_size=256, epochs=15, shuffle=True,  validation_split=0.1)
    return history
history = make_model_3(x_train, y_train, 32, 256)

結果は以下の通り。

Epoch 15/50
45000/45000 [==============================] - 194s - loss: 0.6627 - acc: 0.7702 - val_loss: 0.8667 - val_acc: 0.7092

このモデルはたくさんの多くの層とノードを持っているため、Macbook proの環境だと学習にかなりの時間が掛かるのでepoch 15の時点の結果を抜粋。
validation accuracyが0.7, train accuracyが0.77。
正答率は良い感じだがやはり過学習。（validation accuracyの向上が止まった後もtrain accuracyが上がり続けてた）
この過学習を解消するためのトライ。

def make_model_4(x_train, y_train, conv_num, dense_num):
    input_shape = x_train.shape[1:]

    # make teacher hot-encoded
    y_train = to_categorical(y_train, 10)

    # set model
    model = Sequential()
    model.add(Conv2D(conv_num, (3,3), activation='relu', input_shape=input_shape))
    model.add(Conv2D(conv_num, (3,3), activation='relu'))
    model.add(Dropout(0.2))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Conv2D(conv_num * 2, (3,3), activation='relu'))
    model.add(Conv2D(conv_num * 2, (3,3), activation='relu'))
    model.add(Dropout(0.2))
    model.add(MaxPooling2D(pool_size=(2,2)))

    model.add(Flatten())
    model.add(Dense(dense_num, activation='relu', W_regularizer = l1_l2(.01)))
    model.add(Dropout(0.2))
    model.add(Dense(int(dense_num * 0.6), activation='relu', W_regularizer = l1_l2(.01)))
    model.add(Dense(10, activation='softmax'))
    model.compile(loss=keras.losses.categorical_crossentropy,
              optimizer=keras.optimizers.Adadelta(),
              metrics=['accuracy'])
    # training
    history =model.fit(x_train, y_train, batch_size=256, epochs=15, shuffle=True,  validation_split=0.1)
    return history
history = make_model_4(x_train, y_train, 32, 256)

一次化後の層にl1_l2正則化を設定。過学習の解消しつつ、学習が妨げられないと良いのだが。

結果は以下の通り。

Epoch 15/15
45000/45000 [==============================] - 207s - loss: 3.9736 - acc: 0.5038 - val_loss: 4.0522 - val_acc: 0.4896

epoch 15の段階では過学習は、見られず、正答率はおよそ0.5。
過学習が見られた時のepochが15だったので同じ段階で比較。
正答率の変化のプロットをして確認。

import matplotlib.pyplot as plt
plt.plot(history.history['acc'])
plt.plot(history.history['val_acc'])
plt.ylabel('accuracy')
plt.xlabel('epoch')
plt.legend(['train_accuracy', 'test_accuracy'], loc='best')
plt.show()

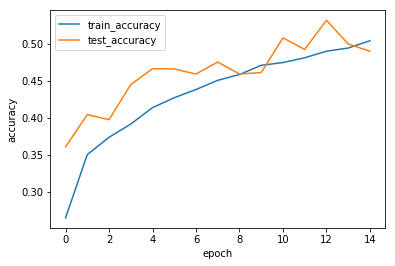
モデルの精度が好ましくないときに考えなけれがいけないは、それがそのネットワークの限界なのか、それとも訓練が足りないだけなのか、ということだが、このようなプロットはその判断を助ける。
この図では、0.4から0.5あたりで正答率の上がりはなだらかになってはいるが、本当にそのあたりで正答率の上限なのかは判断がつかない。
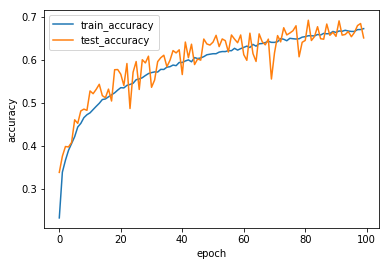
そこで、先ほどのモデルを100 epoch回してみると

Epoch 100/100
45000/45000 [==============================] - 200s - loss: 6.8363 - acc: 0.6719 - val_loss: 6.9292 - val_acc: 0.6504

0.65あたりまでは到達。やはり学習に時間とステップがかかる。この段階では行きすぎた過学習は見られない。