はじめに
ついこの間(2025年4月24~28日)、NeurIPSやICMLに並ぶ AIトップカンファレンスの1つであるICLR 2025がシンガポールで開催されました。ICLRとは2013年にできた新しめの最難関国際会議で、特に表現学習(Representation Learning)分野の研究発表が盛んに行われています。(来年はブラジルのようですね!🇧🇷)
そこで今回『I-Con: A Unifying Framework for Representation Learning (SN Alshammari et.al.)』というICLR 2025で発表されたハイインパクトな論文について、一部ケーススタディ(対照学習、クラスタリング)を混ぜながら紹介したいと思います🐈。
1. I-CONについて
機械学習の研究では近年、表現学習の手法が急増しており、それぞれに独自のアーキテクチャ、損失関数、および学習戦略が用いられています。この断片化により、研究者にとっては異なる手法間の関係を理解し、特定タスクに最適なアプローチを判断することが難しくなっています。
そこでI-CON(Information Contrastive Learning)では、単一の定式化の下で23を超える個別の表現学習手法を統一することに成功し(スゴすぎ)、この複雑な状況に明快さをもたらす包括的な情報理論的フレームワークを提案しています。
つまり埋め込み表現的なものを学習する手法は次元削減、クラスタリング、対照学習など(また教師あり、自己教師あり含め)様々ありますが、これらは全てI-CONというフレームワークの特殊ケースであると主張されているのです。
また何より全ケースに対して数理的な証明・解説が付随してるので、理論的に強固な論文であることがうかがえます。(かなり教育的でありがたいですね。)
2. I-CON フレームワークによる表現学習の統一的な視点
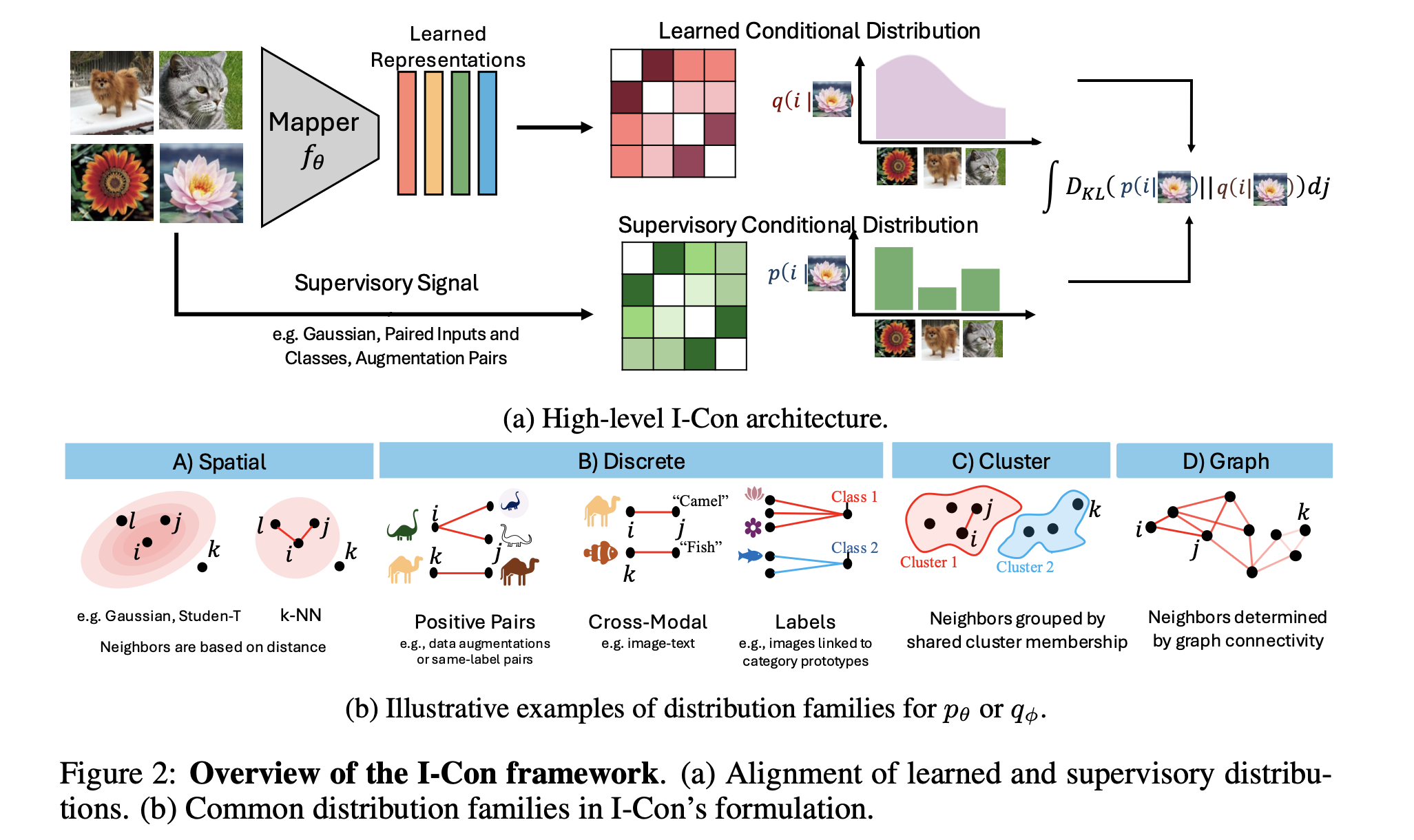
早速ですがI-CON のもたらす理論的なフレームワークについて説明していきます。
I-CON では、表現学習を2つの条件付き確率分布間のKL divergenceの最小化として定式化します。
2つの条件付き確率分布とは次のとおりです。
- $p_\theta(j|i)$: データポイント間の関係をエンコードする教師分布(ターゲット分布やリファレンスモデルとも呼ばれる)
- $q_\phi(j|i)$: 表現空間でモデル化された学習分布
ここで$i$ は「アンカー」データポイント、つまり、焦点を当てている特定のデータポイントを、$j$ はデータセット内の他のデータポイント、または$i$の「近傍」と見なされるデータポイントを指します。
※ また教師モデル$p_\theta(j|i)$に関しては、$\theta$でパラメタライズされていますが、固定されることがほとんどです。
これらを用いてI-CONの目的関数$\mathcal{L}_{\text{I-CON}}$は次のように定義されます。
Definition : I-CONによる表現学習の定式化
\mathcal{L}_{\text{I-CON}} \triangleq \mathbb{E}_i \left[ D_{\mathrm{KL}}\left( p_\theta(j \mid i) \,\|\, q_\phi(j \mid i) \right) \right]
\tag{1}
ここで教師分布$p(j|i)$は、データポイント間の望ましい関係(空間的な近接性、クラスメンバーシップ、拡張ペアなどに基づく)をエンコードし、学習分布$q_\phi(j|i)$は、モデルがこれらの関係をどのようにキャプチャするかを表します。
このスマートな定式化によって、I-CONは多様な手法を分析し理解するための数学的な汎用性を提供することになります。
この損失関数の最小化により、
「データポイントの関係性に関して、正しい確率分布 $p$ と、埋め込み表現が誘導する確率分布 $q_\phi$ を一致させる」
ことを目指します。
次の章では対照学習(Contrastive Learning と クラスタリング(K-means) を例として、I-CONフレームワークがどのようにこれらの既存手法を包摂するかを見ていきます。
3. ケーススタディ① 対照学習
対照学習(Contrastive Learning)は強力な表現学習手法の一つでCV, NLP, Graphといった様々なデータモダリティでかなりホットに研究されています。(自分はこの中だと一番ニッチなグラフ対照学習が専門です笑)
以下では一旦画像のデータについて考えていくことにします。
コアとなる考え方は単純で、簡単に言ってしまえば類似した例の表現を埋め込み空間内で近づけ、非類似な例の表現を遠ざけるというものです。
一般的に対照学習ではデータ$x$に対してAugmentation(データ拡張)といったノイズを付与する操作で別ビュー$\tilde{x}$を作成し、これらを用いて正例(Positive Pair)と負例(Negative Pair)ラベル付けされていない膨大なデータからでも有用な特徴表現を学習することができます。
I-CONフレームワークでは、教師分布 $p(j\mid i)$ と 学習分布 $ q_\phi(j\mid i)$ に関して以下のように定義することで対照学習と等価な学習を実現するとされています。
| 教師分布 $p(j\mid i)$ | 学習分布 $q_\phi(j\mid i)$ | |
|---|---|---|
| 意味 | $x_j=x_i^+$の時のみ1をとるDirac's deltaで設計 | 類似度に基づくsoftmax関数で設計 |
| 式 | $p(j \mid i) \triangleq \delta_{ji+}$ | $ q_\phi(j\mid i) \triangleq \dfrac{\exp\bigl(f_\phi(x_i) \cdot f_\phi(x_j)/\tau\bigr)}{\sum_{m\neq i}\exp\bigl(f_\phi(x_i)\cdot f_\phi(x_m)/\tau\bigr)} $ |
| 備考 | 同一画像の別ビューのみが正例となる | インデックス$i$のデータに対してデータ$j$が正例となる確率を示す |
※ この時埋め込みは $ ||f_\phi(x)|| = 1 $ で正規化し、シミラリティは埋め込み間の内積で定義されるとします。(大体Projection Headによって超球面上に射影されることが多いです。)
3.1 InfoNCE 損失
一般にSimCLR など対照学習手法では以下のような InfoNCE と言う正例ペアのシミラリティに対してsoftmaxをとった以下のような形式の損失関数が用いられます。
\mathcal{L}_{\mathrm{InfoNCE}}
\triangleq -\sum_i \log
\frac{\exp\bigl(f_\phi(x_i)\!\cdot\!f_\phi(x_i^+)/\tau\bigr)}
{\sum_{m}\exp\bigl(f_\phi(x_i)\!\cdot\!f_\phi(x_m)/\tau\bigr)}
\tag{2}
ここで $i^+$ はサンプル $i$ の正例インデックスです。
このInfoNCE 損失を、$p$と$q$のクロスエントロピー形式に展開することを考えます。
\begin{aligned}
\mathcal{L}_{\mathrm{InfoNCE}}
&= -\sum_i
\log\frac{\exp(f_\phi(x_i)\!\cdot\!f_\phi(x_i^+)/\tau)}
{\sum_m \exp(f_\phi(x_i)\!\cdot\!f_\phi(x_m)/\tau)} \\[4pt]
&= -\sum_i
\log q_\phi(i^+\mid i) \\[4pt]
&= -\sum_{i,j} p(j\mid i)\,\log q_\phi(j\mid i) \\[4pt]
&= H(p,\;q_\phi).
\end{aligned}
\tag{3}
ここで 途中で導入した $p(j\mid i)$ は Dirac's deltaで
p(j\mid i)=
\begin{cases}
1 & (j = i^+)\\
0 & \text{otherwise}
\end{cases}
となります。
3.2 KL divergenceの 最小化
さて、KL divergenceで定義づけられたI-CON損失 $\mathcal{L}_{\text{I-CON}}$ についてみていきましょう。
KL を自己エントロピー $H(p)$とクロスエントロピー $H(p,q_\phi)$ に分解します。
\begin{aligned}
D_{\mathrm{KL}}(p\Vert q_\phi)
&= \sum_{i,j} p(j\mid i)\,\log\frac{p(j\mid i)}{q_\phi(j\mid i)} \\[4pt]
&= -\underbrace{\sum_{i,j} p(j\mid i)\,\log q_\phi(j\mid i)}_{H(p,q_\phi)}
\;+\; H(p) \\[4pt]
&= H(p,q_\phi) - H(p).
\end{aligned}
\tag{4}
今回$p$ は固定なので、$H(p)$ は定数になりますね。
したがって(3) 式と(4) 式から
\mathcal{L}_{\mathrm{InfoNCE}}
\;\propto\;
\mathcal{L}_{\text{I-CON}}
となり、
\min_\phi \mathcal{L}_{\mathrm{InfoNCE}}
\;\Longleftrightarrow\;
\min_\phi D_{\mathrm{KL}}(p\Vert q_\phi).
が言えます。
つまりSimCLR 等の 対照学習によるInfoNCE損失の最小化 は I-CONフレームワークの特殊ケースである とみなせます。
4. ケーススタディ② クラスタリング(K-means)
続いてクラスタリングでお馴染みのK-meansの場合についてです。
「K-means はクラスター中心との距離を最小化するだけの古典的クラスタリングだ...」 そう思っていると 他手法とのつながりが見えませんよね🧐
実は “確率化 → 対照形式化 → KL 化” と 3 つのステップを経ると同様のI-CON形式に落ち着きます。
4.1 古典的 K-means
K-meansでは一般的に以下のステップに従いクラスタリングを行います。
-
データ点 $x_i\in\mathbb R^d$ $(
i=1,\dots,N)$に対して、まずは適当にクラスターを$m$個割り当てる。 -
各クラスターに対してクラスター中心と呼ばれる重心 $\mu_c$ $( c=1,\dots,m )$ を計算する。
-
各点に対して重心からの距離を計算し、距離が一番近いクラスタに割り当て直す。
-
収束したら(変化がなくなったら)終了。
さて、上記のアルゴリズムについては、以下の損失関数を定義して、それの最小化を行う過程で導出されます。
\displaystyle
\mathcal L_{\text{k-Means}}
\triangleq \sum_{i=1}^{N}\sum_{c=1}^{m}
\mathbf 1[c(i)=c]\;\|x_i-\mu_c\|^{2},
\qquad
c(i)=\arg\min_c \|x_i-\mu_c\|^{2}.
この式で、$\mathbf 1[c(i)=c]$ の部分で、一番近い中心へハードに割り当てられ、距離²の総和を最小化するようになります。
4.2 確率的 K-means ― 凸緩和と “ゼロギャップ”
固定的なK-meansでは最も距離の近い中心へハードに割り当てられていましたがこれを連続的な確率ベクトル にソフトに緩和することができます。
この時ソフトな K-means の損失関数は以下のように定義されます。
\displaystyle
\mathcal L_{\text{Prob-kM}}
\triangleq \sum_{i=1}^{N}\sum_{c=1}^{m}
\phi_{ic}\,\|x_i-\mu_c\|^{2},
\quad
\phi_{ic}\ge0,\;\sum_c\phi_{ic}=1.
これは元の問題の 凸緩和(中心 $\mu_c$ を固定したとき)であり、最適化すると結局 $\phi_{ic}\in{0,1}$ に収束します。 ⇒ “ギャップ 0”。
Proof idea: 各 $x_i$ に対して距離が最小のクラスタへ質量を押し込むのが常に有利。
ここまでで K-means を “連続最適化” で扱う土台が完成。
4.3 対照形式への再構成
K-meansの確率化ができたので、次に対照形式に定式化することを考えます。
まず、サンプリング点$x_j$が$x_i$と同じクラスターから抽出されるクラスタ共起確率$q_\phi(j \mid i)$ を条件付き確率として求めます。
「同じクラスタから 1 点だけ無作為に取り出す」という 2 段階過程
- クラスタ $c$ を $P(C=c\mid i)=\phi_{ic}$ で選ぶ
- そのクラスタの中から $x_j$ を一様(ソフトなら重み付き)に選ぶ
q_\phi(j\mid i)
= \sum_{c=1}^{m}
\frac{\phi_{ic}\,\phi_{jc}}{\sum_{k} \phi_{kc}}.
これが 「$i$ と $j$ が同じクラスタから出る確率」 になります。
また、データ点$x_i$とクラスタ中心 $\mu_c$で表現される $\mathcal L_{\text{Prob-kM}}$ は データ点同士の$x_i, x_j$ペアの距離で
\mathcal L
=\sum_{i}\mathcal L_i
=-\sum_{i,j} ||x_i - x_j||^2\;q_\phi(j\mid i).
と書き換えられます。(細かい証明は省略)
4.4 I-CON フレームワークに変換
これで準備は整ったので、次はI-CONフレームワークで$p, q$ に関して以下のように定式化を行います。
| 教師分布 $p(j\mid i)$ | 学習分布 $q_\phi(j\mid i)$ | |
|---|---|---|
| 意味 | データ点ペアの$x_i,x_j$の距離に対してsoftmaxをとった関数(ガウスカーネル) | サンプリング点$x_j$が$x_i$と同じクラスターから抽出されるクラスタ共起確率 |
| 式 | $p_\theta(j\mid i) \triangleq \frac{\exp \bigl(-|x_i-x_j|^{2}/2\sigma^{2})}{\sum_{k}\exp\bigl(-|x_i-x_k|^{2}/2\sigma^{2})}$ | $ q_\phi(j\mid i)\triangleq \sum_{c=1}^{m}\frac{\phi_{ic},\phi_{jc}}{\sum_{k} \phi_{kc}} $ |
ここで$p_\theta(j \mid i)$について、簡単のため $2\sigma^2=1$、分母の正規化項を$Z_i$ として対数をとって変形すると、以下のようになります。
\log p_\theta(j \mid i)
= -\lVert x_i - x_j \rVert^2 \;-\;\log Z_i.
また今回の$q,p$間のKLを以下のように$\mathcal L_{\text{c-SNE}}$と定義しておきます。
\mathcal L_{\text{c-SNE}} \triangleq \sum_i
D_{\mathrm{KL}}\bigl(q_\phi(\cdot\mid i)\,\|\,p_\theta(\cdot\mid i)\bigr)
ここで上で定義した$\mathcal{L}_i$について、以下のように変形することで、KLとエントロピーを用いて表現することができます。
\begin{aligned}
\mathcal{L}_i
&= -\sum_j \lVert x_i - x_j \rVert^2 \, q_\phi(j \mid i)\\
&= \sum_j \bigl(\log p_\theta(j \mid i) + \log Z_i\bigr)\,q_\phi(j \mid i)\\
&= \sum_j q_\phi(j \mid i)\,\log p_\theta
(j \mid i) + \log Z_i\\
&= H\bigl(q_\phi(\cdot\mid i),\,p_\theta(\cdot\mid i)\bigr) + \log Z_i\\
&= D_{\mathrm{KL}}\bigl(q_\phi(\cdot\mid i)\,\|\,p_\theta(\cdot\mid i)\bigr)
+ H\bigl(q_\phi(\cdot\mid i)\bigr)
+ \log Z_i
\end{aligned}
よって、
\begin{aligned}
\mathcal{L}_{\mathrm{Prob\text{-}KMeans}}
&= - \sum_i \sum_j \lVert x_i - x_j \rVert^2 \, q_\phi(j \mid i)
= \sum_i \mathcal{L}_i\\
&= \sum_i \Bigl[
D_{\mathrm{KL}}\bigl(q_\phi(\cdot\mid i)\,\|\,p_\theta(\cdot\mid i)\bigr)
+ H\bigl(q_\phi(\cdot\mid i)\bigr)
+ \log Z_i
\Bigr]\\
&= \mathcal{L}_{\mathrm{c-SNE}}
+ \sum_i H\bigl(q_\phi(\cdot\mid i)\bigr)
+ \mathrm{const}
\end{aligned}
が得られます。
したがって、
\min_\phi \mathcal{L}_{\mathrm{InfoNCE}}
\;\Longleftrightarrow\;
\min_\phi \mathcal{L}_{\mathrm{c-SNE}}
が言えます。
つまり K-meansクラスタリングの損失関数最小化 は I-CONフレームワークの特殊ケースである とみなせます。
ちなみに 温度パラメータ(分散)$\sigma$をそのまま用いると
\boxed{
\displaystyle
\mathcal L_{\text{c-SNE}}
= \frac{1}{2\sigma^{2}}\,
\mathcal L_{\text{Prob-kM}}
- \sum_{i=1}^{N} H\!\bigl(q_\phi(\cdot\mid i)\bigr),
}
\qquad
H(q)=-\!\sum_j q(j)\log q(j).
のように$\mathcal L_{\text{c-SNE}}$は $\mathcal L_{\text{Prob-kM}}$を用いて表現できます。
- 前項 : 距離²の重み付き和(= Prob-k-Means の損失)
-
後項 : 負のエントロピー制約
- エントロピーを 小さく したい ⇒ 割り当てが 0/1(ハード) に近づく
- $\sigma \downarrow $ で距離項が強まり、相対的に制約も強まる
(温度パラメータ $\sigma$ は Soft ↔ Hard のダイヤルになってることがわかりますね!)
5. まとめ
『I-Con: A Unifying Framework for Representation Learning (SN Alshammari et.al.)』というICLR2025の論文を紹介してみました。
普段馴染みのある表現学習手法が、全て1つの目的関数で定式化され、それらの特殊ケースであるというのは驚きでしたね。
今回、対照学習とK-meansクラスタリングの2つの事例に関して I-CON最適化との等価性を示しましたが、確率モデルで考える場合クロスエントロピーがKLの形に接続するKeyになっていましたね〜(教師分布の方の$p \log p$が定数になるので当たり前な感想かもしれません笑)。
実は自分のグラフ対照学習の研究でも、I-CONの定式化に則って新たな"教師あり"グラフ対照学習:SupGCL (Supervised Graph Contrastive Learning)を開発し、既存手法の理論的拡張に成功しました。(I-CONには大変お世話になりました🙇)
また論文も読みやすく、数式も丁寧なので大変勉強になりました。ぜひ興味を持った方はフルペーパーで読んでいただけたらと思います。
6. 参考文献
『I-Con: A Unifying Framework for Representation Learning (SN Alshammari et.al.)』
↓ Openreview版
↓ Arxiv版