こちらはTensorFlow Advent Calendar 2016の2日目です。
書いている人は、今年の4月に機械学習のこともよくわからない状態からディープラーニングを中心に勉強し始めて、最近少しは使えるようになってきたかなという感じです。
勢いでアドベントカレンダーにエントリーしたものの、あまり難しいことはマサカリが飛んでくる力が及ばないと思うので、これからディープラーニングやTensorFlow始めようかなという人向けの記事にします。読んでみて、「自分もディープラーニング始めてみようかな」「TensorFlow触ってみようかな」と思ってもらえれば嬉しいです。
想定している読者
プログラミング経験はあるけど、機械学習・ディープラーニングは全くわからないという人に向けて書いています。
使用している言語はPythonですが、リスト内包表記とNumPy以外は他の言語経験があればそれほど問題なく理解できると思います。
リスト内包表記というのは
a = []
for i in array:
a.append(i)
というのを
a = [i for i in array]
と書く方法です。
NumPyはX[:, 0, 1]のような形式で、多次元配列を扱いやすくしたものだと思えばとりあえず大丈夫です。おそらく学習過程を可視化した部分にしか出てこないと思うので、最初はあまり気にしないでください。
記事の目的
ディープラーニングってバズってて興味あるけど、難しそうとか数学の事前知識ないと始められなさそうとか二の足を踏んでいる人に、意外と簡単に始められそうと思ってもらうのが目的です。
とりあえず、以下で線形回帰(機械学習で最初のほうに習う手法)を3回拡張してディープラーニングのHello World的な多層パーセプトロンを作ってみます。
ついでに、素のTensorFlowを書いて構造を理解するのは初心者には辛いので、簡潔に書けて仕組みがわかりやすいライブラリであるtf.learnとtf.slim(TensorFlow標準搭載)を使っていきます。
サンプルコードを実行すると機械が学習している様子がアニメーションで視覚化されます。とりあえずコードに何が書かれているのか、どういう仕組みなのかはわからなくてもいいのでコピペで実行してみてください。(ちなみにTensorFlow Playgroundならもう少し簡易なものがコピペすら不要でブラウザから実行できます。)
それで興味を持ったら、ぜひアルゴリズムやコードの中身を調べてみてください。
MyMonitorクラスは可視化のために作成しただけなので、そこは無視しちゃって構いません。
tf.learn・tf.slim関連(TensorFlowを使ったことある人向け)
今回の記事は完全初学者向けの内容ですが、tf.learn・tf.slimについてだけは少し紹介しておきます。TensorFlowを使ったことのない人は、このパートは飛ばしてください。
tf.learn(tf.contrib.learn)は、学習や予測を簡単にしてくれるライブラリです。scikit-learnのようにモデルを作成し、fitするだけで学習できます。簡単な学習を行うだけなら、GraphやSessionを明示的に意識する必要もなくなります。
基本的にはEstimatorクラスにモデルを与えてインスタンス化し、fitするという流れです。KerasやTFLearnと似ています。TFLearnなんて名前も似ているし、中身もtf.learn+tf.slimのようなものですが、別物です。
Estimatorクラスに与えるモデルは戻り値として、predictで実行結果として返す変数・損失を表すTensor・TrainOpを表すTensorの3つを返さないといけません。TrainOpはslim.optimize_lossを利用するか、optimizer.minimizeを実行した後のTensorを渡せばよかったかと思います。
fitの際にmonitorsという引数にlearn.monitors.BaseMonitorやlearn.monitors.EveryNを継承したクラスのインスタンスを配列で渡すと、学習途中でコールバック関数のように使えます。learn.monitors.get_default_monitorsで、一般的にtensorboardで可視化したいことが多いものを返してくれるらしいので、とりあえずはこれを渡しておいてもいいと思います。
今回monitorsは、学習の途中経過を視覚化するのに利用しただけです。
学習途中でpredictを実行したところ、モデルの変数はfitの最中には更新されないみたいだったので、step_endでその時点の値を取り出して自力で計算しています。learn.inferを使うとできそうな雰囲気もあるのですが、使い方がいまいちわからなかったので今回は使えませんでした。
学習途中でpredictしたいというニーズも少ないでしょうが、Batch Normalizationを入れたりして複雑になってくると間違いやすくなるので、別のGraphに作った同一のモデルに対して変数の値を更新してpredictするといいかもしれません。
step_endのoutputsで利用したい変数はstep_beginでTensorの名前を指定しないといけません。コードを全部書き終わってから気づきましたが、learn.Estimator.get_variable_names()で変数名一覧取得できたみたいです。ただ、スコープで絞り込むといった操作には対応していないようです。
ちなみに、tf.learnのpredictはas_iterable=Trueが今後デフォルトになるようです。この場合、predictは値ではなくGenerator(かな?)を返すようで、値を取得したいときは[v for v in estimator.predict(x)]とやれば大丈夫です。ただ、これだとpredictの実行が遅い気がするのですが、どうしてこうなったんでしょう?
tf.slim(tf.contrib.slim)は、主に畳み込みニューラルネットワークを書きやすくするためのライブラリです。非常に便利なのですが、開発途中でまともなドキュメントもないので使いこなそうとするとGithubのリポジトリをさまようことになります。
tf.slimを利用するのは主に各層の定義時かと思いますが、その場合はtf.contrib.layersを見るといいです。
Batch Normalizationを使う場合は、normalizer_fn=slim.batch_normとすればいいでしょう。activation_fnの規定値はReLUです。ここはSoftmax通すときにうっかり意図せずReLUが適用されてしまうことがあるので、規定値はLinearにしてほしいところです。
tf.learn・tf.slimともに生TensorFlowと混ぜて使っても問題ありません。
実行環境
MacBook
Python 3.5.2
TensorFlow 0.11.0rc2 (CPU only)
NumPy 1.11.2
scikit-learn 0.18
matplotlib 1.5.3
Jupyter Notebookも公開してあります。
スタート:線形回帰
機械学習のタスク(コンピュータに予測してもらいたい問題)の代表的なものに分類と回帰があります。
分類も回帰も与えられたデータから何かを予測するのですが、予測する内容が異なります。分類というのはカテゴリ、回帰というのは数値の予測が目的です。エンジニアだと、予測対象が文字列型なら分類、数値型なら回帰というイメージでもいいかもしれません。
具体的な例を挙げると、
- 回帰
- 天気・気温・季節・最近の売り上げから、次の日の売り上げ(仕入れ)を予測
- 分類
- 含まれる単語の種類・頻度から、記事のカテゴリ予測や迷惑メール仕分け
ここで取り扱う線形回帰は名前から予想できる通り回帰問題のためのアルゴリズムで、その中でも最も基本的なものです。
具体的には、 $x_1,\ x_2,\ ...\ x_n$ という入力の場合は $y$ であるというデータがあるときに
$w_1x_1\ +\ w_2x_2\ +\ ...\ w_nx_n\ +\ b\ {\approx}\ y$
となるような $w_1,\ w_2,\ ...\ w_n,\ b$ を求め、未知の $x_1',\ x'_2,\ ...\ x'_n$ に対して $y'$ を予想します。
翌日の売り上げを予測する例では
| 気温($x_1$) | 時期($x_2$) | $...$ | 前日売上($x_n$) | 翌日売上($y$) |
|---|---|---|---|---|
| 15度 | 9月 | ... | 100万円 | 120万円 |
| 30度 | 8月 | ... | 90万円 | 85万円 |
| ... | ... | ... | ... | ... |
| 20度 | 6月 | ... | 95万円 | ??? |
のようになります。
コードで書くと、
"""
xとwは同じ長さの配列
bは実数
"""
def linear(x, w, b):
return sum([x[i] * w[i] for i in range(len(x))]) + b
y = linear(x, w, b)
という感じです。
どうやって $w$ や $b$ を求めるのかは長くなるので気にしなくていいです。とりあえずサンプルコードで学習が進む様子を可視化してみたので、それがおもしろいと思って気になったら調べてみてください。
$w_1x_1\ +\ w_2x_2\ +\ ...\ w_nx_n\ +\ b$ と毎回書くのはだるい冗長ですが、行列(線形代数)を利用すると、 $X\ {\times}\ W\ +\ b$ のように簡潔に表せます。これ自体は単なる書き方の規則だと思えばいいでしょう。
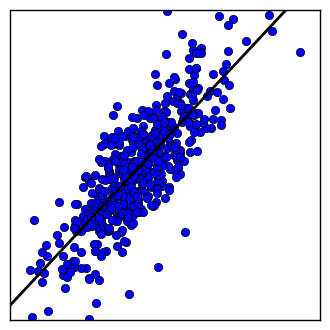
サンプルコードでは、入力される特徴 $x$ は1つだけで、そこから $y$ を予測します。横軸が $x$ 、縦軸が $y$ で、沢山ある点は入力データの分布です。直線は学習の結果得られた入力 $x$ に対する $y$ の予測です。学習が進んでいくと、直線が点の真ん中あたりを通って行くようになるはずです。
コード
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
learn = tf.contrib.learn
slim = tf.contrib.slim
from sklearn.datasets import make_regression
plt.ion()
X, y = make_regression(n_samples=500, n_features=1, noise=25.0, random_state=12345)
X, y = X.astype(np.float32), y.astype(np.float32)
def my_model(X, y):
y = tf.reshape(y, [-1, 1])
prediction = slim.fully_connected(X, 1, activation_fn=None, scope='fc')
loss = slim.losses.mean_squared_error(prediction, y)
train_op = slim.optimize_loss(loss, slim.get_global_step(), learning_rate=0.01, optimizer='SGD')
return tf.reshape(prediction, [-1]), loss, train_op
class MyMonitor(learn.monitors.BaseMonitor):
def begin(self, max_steps):
self.figure = plt.figure(figsize=(4, 4))
self.x_min, self.x_max = X.min() - .5, X.max() + .5
self.y_min, self.y_max = y.min() - .5, y.max() + .5
def step_begin(self, step):
return ['fc/weights', 'fc/biases']
def step_end(self, step, outputs):
self.figure.clf()
plt.xlim(self.x_min, self.x_max)
plt.ylim(self.y_min, self.y_max)
plt.xticks(())
plt.yticks(())
plt.plot(X, y, "o")
w = outputs['fc/weights'][0][0]
b = outputs['fc/biases'][0]
px = np.array([self.x_min, self.x_max])
py = px * w + b
plt.plot(px, py, color='k', linestyle='-', linewidth=2)
self.figure.canvas.draw()
def end(self):
pass
regressor = learn.Estimator(model_fn=my_model, model_dir='/tmp/my_model/linear_regression')
regressor.fit(x=X, y=y, steps=500, batch_size=128, monitors=[MyMonitor()])
興味が湧いて調べてみたい場合のキーワード
- slim.fully_connectedがやっているのは、上のほうで書いたlinearという関数と同じです。
- 確率的勾配降下法(SGD = Stochastic Gradient Descent)を二乗平均誤差(Mean Squared Error)を使って学習しています。
ステップ1:単純パーセプトロン
線形回帰は $w_1x_1\ +\ w_2x_2\ +\ ...\ w_nx_n\ +\ b\ {\approx}\ y$ という風に表せましたが、この $y$ に活性化関数を適用するとニューラルネットワークの最小単位である単純パーセプトロンになります。
活性化関数というのは例えば $f(x)\ =\ \begin{cases} 1 & (\ x\ >\ 0\ ) \newline 0 & (\ x\ \le\ 0\ ) \end{cases}$ のような関数 $f(x)$ を指します。活性化関数には非線形な(直線じゃない)ものを通常使いますが、問題が回帰の場合は最後の出力層の活性化関数を線形 $\left(\ f(x)\ =\ x\right)$ にすることもあるようです。
コードで書くと、
def linear(x, w, b):
return sum([x[i] * w[i] for i in range(len(x))]) + b
def activation(x):
return 1 if x > 0 else 0
y = activation(linear(x, w, b))
という感じです。
単純パーセプトロンは、活性化関数次第で分類にも回帰にも使えます。例えば、 $f(x)\ =\ \mathrm{e}^x$ とすると、正の値をとる回帰問題に適用できるかもしれません。(線形回帰も少し手を加えると分類に使えますが)
今回はシグモイド関数$\left(\ f(x)\ =\ \frac{1}{1\ +\ \mathrm{e}^{-x}}\ \right)$を使って、分類問題に挑戦してみます。これは(2クラス)ロジスティック回帰と呼ばれるものです。回帰という名前がついていますが、分類のアルゴリズムです。
シグモイド関数は、入力 $x$ に対して $0\ <\ y\ <\ 1$ となる値を返し、この $y$ は実質的にその分類への確信度(確率)と捉えられます。
線形回帰のときと同じように、入力 $x_1,\ x_2,\ ...\ x_n$ の場合は $y$ というデータから学習し、 $x'_1,\ x'_2,\ ...\ x'_n$ の場合は $y'$ という予測を行います。ただし、ロジスティック回帰では $y$ は $0$ または $1$ という値しかとりません。
迷惑メールを分類する例では
| お金($x_1$) | 副業($x_2$) | ... | 高収入($x_n$) | 迷惑メールかどうか($y$) |
|---|---|---|---|---|
| 0.3 | 0.2 | ... | 0.4 | 1 (迷惑メール) |
| 0.5 | 0.0 | ... | 0.001 | 0 (迷惑メールじゃない) |
| ... | ... | ... | ... | ... |
| 0.4 | 0.1 | ... | 0.0 | ??? |
のような感じです。
入力 $x$ の値は、メールの全単語中にその単語が現れる頻度です。また、学習時に与えられる $y$ は 0 (迷惑メールじゃない) か 1 (迷惑メール) かで与えられますが、予測 $y'$ は 0.7 (70%の確率で迷惑メール) のような数値で得られます。
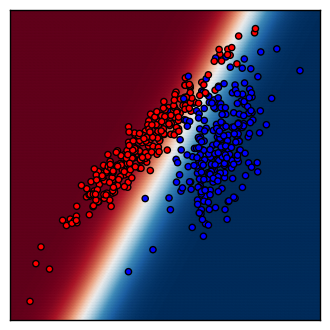
サンプルコードでは、2つの特徴 $x$ に基づいて、 $x_1$ を横軸・ $x_2$ を縦軸にとってデータの分布図を描いています。各点の色は正解 $\left(\ y\ =\ 0\ or\ 1\ \right)$ の分類を表しています。背景の色は、そのエリアをどちらに分類しようとしているかを表し、色が濃いほど確信を持って分類しています。
コード
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
learn = tf.contrib.learn
slim = tf.contrib.slim
from sklearn.datasets import make_regression
plt.ion()
X, y = make_classification(n_samples=500, n_features=2, n_redundant=0, n_informative=2, n_clusters_per_class=1, random_state=345678)
X, y = X.astype(np.float32), y.astype(np.uint8)
def my_model(X, y):
y = tf.reshape(y, [-1, 1])
logit = slim.fully_connected(X, 1, activation_fn=None, scope='fc')
prob = tf.sigmoid(logit)
prob = tf.reshape(prob, [-1])
loss = slim.losses.sigmoid_cross_entropy(logit, y)
train_op = slim.optimize_loss(loss, slim.get_global_step(), learning_rate=0.1, optimizer='SGD')
return {'class': tf.cast(tf.round(prob), tf.uint8), 'prob': prob}, loss, train_op
class MyMonitor(learn.monitors.BaseMonitor):
def begin(self, max_steps):
self.figure = plt.figure(figsize=(4, 4))
self.cm = plt.cm.RdBu
self.cm_scatter = ListedColormap(['#FF0000', '#0000FF'])
self.x_min, self.x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
self.y_min, self.y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
self.xx, self.yy = np.meshgrid(np.arange(self.x_min, self.x_max, .02), np.arange(self.y_min, self.y_max, .02))
self.xx, self.yy = self.xx.astype(np.float32), self.yy.astype(np.float32)
self.grid = np.c_[self.xx.ravel(), self.yy.ravel()]
def step_begin(self, step):
return ['fc/weights', 'fc/biases']
def step_end(self, step, outputs):
self.figure.clf()
plt.xlim(self.x_min, self.x_max)
plt.ylim(self.y_min, self.y_max)
plt.xticks(())
plt.yticks(())
w = outputs['fc/weights']
b = outputs['fc/biases']
logit = self.grid.dot(w) + b
logit = logit.reshape(self.xx.shape)
z = self.sigmoid(logit)
plt.scatter(self.xx.ravel(), self.yy.ravel(), c=z, cmap=self.cm, marker='.', alpha=0.8, linewidths=0.01)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=self.cm_scatter)
self.figure.canvas.draw()
def end(self):
pass
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
classifier = learn.Estimator(model_fn=my_model, model_dir='/tmp/my_model/perceptron')
classifier.fit(x=X, y=y, steps=500, batch_size=128, monitors=[MyMonitor()])
興味が湧いて調べてみたい場合のキーワード
- 確率的勾配降下法(SGD)をシグモイド関数(Sigmoid)と交差エントロピー誤差(Cross Entropy Loss)を使って学習しています。
ステップ2:(多クラス)ロジスティック回帰
ここまでは、最終的な出力 $y$ は1つだけでしたが、シグモイド関数の親戚であるソフトマックス関数 $\left(\ f(x)\ =\ \frac{\mathrm{e}^{x_i}}{\sum_{j=1}^{n}\mathrm{e}^{x_j}},\ i\ =\ 1,\ 2,\ ...\ n\ \right)$ を利用すると、多クラス分類が利用可能です。( $n$ は分類したいクラスの数)
ソフトマックス関数は $n$ 個の値 $y_1,\ y_2,\ ...\ y_n$を出力しますが、各出力はやはり $0\ <\ y_i\ <\ 1$ の確率であり、全ての出力を合計すると1 $\left(\sum_{i=1}^{n}y_i\ = 1\right)$ になります。
また例をあげると、
| オラ($x_1$) | 腹減った($x_2$) | ... | やれやれ($x_n$) | 孫悟空($y_1$) | 空条承太郎($y_2$) | その他($y_3$) |
|---|---|---|---|---|---|---|
| 0.2 | 0.5 | ... | 0.1 | 0.9 | 0.09 | 0.01 |
| 0.9 | 0.005 | ... | 0.09 | 0.05 | 0.9 | 0.05 |
| ... | ... | ... | ... | ... | ... | ... |
| 0.01 | 0.9 | ... | 0.02 | ??? | ??? | ??? |
という感じです。
各変数の意味は迷惑メール分類のときと同じです。
複数の値を出力する場合、出力したい値の数に応じてパーセプトロンを並列に並べます。この1つ1つのパーセプトロンをノードと呼びます。それぞれのノードは異なる $w,\ b$ を持ちます。
例えば、入力を $x_1,\ x_2,\ ...\ x_n$ とし、2つの値を出力するために $a_1,\ a_2$ という2つのノードを用意します。活性化関数を $f(x)$ とすると $a_1,\ a_2$ それぞれの出力は
$a_1\ =\ f(\ w_{11}x_1\ +\ w_{12}x_2\ +\ ...\ w_{1n}x_n\ +\ b_1\ )$
$a_2\ =\ f(\ w_{21}x_1\ +\ w_{22}x_2\ +\ ...\ w_{2n}x_n\ +\ b_2\ )$
です。
コードで書くと、
"""
特徴xの種類をm、分類したいクラスの数をnとすると
x[m], w[n][m], b
"""
from math import exp
def linear(x, w, b):
return sum([x[i] * w[i] for i in range(len(x))]) + b
def softmax(x):
e = [exp(x[i]) for i in range(len(x))]
s = sum(e)
return [e[i] / s for i in range(len(x))]
y = softmax([linear(x, w[i], b) for i in range(len(x))])
という感じです。
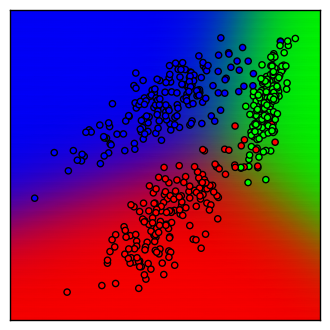
サンプルコードを実行すると3クラスのデータが分布図に描かれるはずです。単純パーセプトロンのときと同じように、RGBの原色に近いエリアほど確信を持って分類しています。
コード
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
learn = tf.contrib.learn
slim = tf.contrib.slim
from sklearn.datasets import make_classification
from matplotlib.colors import ListedColormap
plt.ion()
n_class = 3
X, y = make_classification(n_samples=500, n_features=2, n_informative=2, n_redundant=0, n_classes=n_class, n_clusters_per_class=1, random_state=234567)
X, y = X.astype(np.float32), y.astype(np.uint8)
def my_model(X, y):
y = slim.one_hot_encoding(y, n_class)
logit = slim.fully_connected(X, n_class, activation_fn=None, scope='fc')
prob = slim.softmax(logit)
loss = slim.losses.softmax_cross_entropy(logit, y)
train_op = slim.optimize_loss(loss, slim.get_global_step(), learning_rate=0.1, optimizer='SGD')
return {'class': tf.argmax(prob, 1), 'prob': prob}, loss, train_op
class MyMonitor(learn.monitors.BaseMonitor):
def begin(self, max_steps):
self.figure = plt.figure(figsize=(4, 4))
self.cm_scatter = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
self.x_min, self.x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
self.y_min, self.y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
self.xx, self.yy = np.meshgrid(np.arange(self.x_min, self.x_max, .02), np.arange(self.y_min, self.y_max, .02))
self.xx, self.yy = self.xx.astype(np.float32), self.yy.astype(np.float32)
self.grid = np.c_[self.xx.ravel(), self.yy.ravel()]
def end(self):
pass
def step_begin(self, step):
return ['fc/weights', 'fc/biases']
def step_end(self, step, outputs):
self.figure.clf()
plt.xlim(self.x_min, self.x_max)
plt.ylim(self.y_min, self.y_max)
plt.xticks(())
plt.yticks(())
w = outputs['fc/weights']
b = outputs['fc/biases']
logit = self.grid.dot(w) + b
logit = logit.reshape([-1, n_class])
prob = self.softmax(logit)
plt.scatter(self.xx.ravel(), self.yy.ravel(), c=prob, marker='.', alpha=0.8, linewidths=0.01)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=self.cm_scatter)
self.figure.canvas.draw()
def softmax(self, x):
e = np.exp(x)
sum = e.sum(axis=1)
sum = np.repeat(sum.reshape([-1, 1]), 3, axis=1)
return e / sum
classifier = learn.Estimator(model_fn=my_model, model_dir='/tmp/my_model/logistic_regression')
classifier.fit(x=X, y=y, steps=100, batch_size=128, monitors=[MyMonitor()])
興味が湧いて調べてみたい場合のキーワード
- 確率的勾配降下法(SGD)をソフトマックス関数(Softmax)と交差エントロピー誤差(Cross Entropy Loss)で学習しています。
- slim.fully_connectedの2番目の引数が初めて変わったことからわかるように、この値は出力の個数を表します。
ステップ3:多層パーセプトロン
入力と出力の間に中間層(隠れ層)を追加すると、ディープラーニングの完成です。
中間層が加わることで、非線形(直線では分類できない)・複雑な問題に対応できます。
コードで書くと、
"""
入力xの種類をm、分類したいクラス数をn、中間層のノード数をoとすると
x[m], w1[o][m], b1, w2[n][o], b2
"""
from math import exp
def linear(x, w, b):
return sum([x[i] * w[i] for i in range(len(x))]) + b
def layer_fn(x, w, b, activation_fn):
return activation_fn([linear(x, w[i], b) for i in range(len(x))])
def relu(x):
return [x[i] if x[i] > 0 else 0 for i in range(len(x))]
def softmax(x):
e = [exp(x[i]) for i in range(len(x))]
s = sum(e)
return [e[i] / s for i in range(len(x))]
h = layer_fn(x, w1, b1, relu)
h = layer_fn(h, w2, b2, softmax)
という感じです。
入出力はロジスティック回帰のときと変わらないので、特に例はあげません。
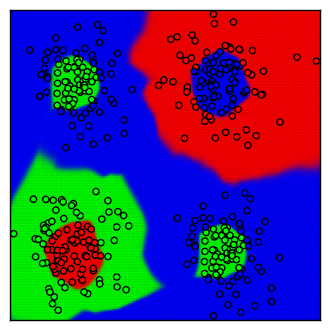
サンプルコードの中間層はノード数30のものを5層入れています。
中間層というのはロジスティック回帰のようなニューラルネットワークの入力と出力の間に挟み込むニューラルネットワークです。あるいは、1つのニューラルネットワークの出力を次のニューラルネットワークの入力にして……(以下繰り返し)という構成になっているものの最初と最後以外とも言えます。
入力→中間層→中間層→...→出力のように通常はいくつも中間層を重ねます。このように層をいくつも重ねてネットワークの構成を深くしていくので、ディープニューラルネットワーク・ディープラーニングと呼ばれます。
中間層の活性化関数にはReLUを使用しています。ReLUは $f(x)\ =\ \begin{cases} x & (\ x\ >\ 0\ ) \newline 0 & (\ x\ \le\ 0\ )\end{cases}$ というものです。
コード
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
learn = tf.contrib.learn
slim = tf.contrib.slim
from sklearn.datasets import make_gaussian_quantiles
from matplotlib.colors import ListedColormap
plt.ion()
n_class = 3
n_cluster = 2
n_step = 20000
tf.set_random_seed(0)
for row, mean_x in enumerate(np.linspace(-2.0, 2.0, n_cluster)):
for col, mean_y in enumerate(np.linspace(-2.0, 2.0, n_cluster)):
step = row + col
new_X, new_y = make_gaussian_quantiles(mean=(mean_x, mean_y), cov=0.4, n_samples=100, n_features=2, n_classes=2, random_state=step)
new_y += step
new_y = np.mod(new_y, n_class)
if step == 0:
X, y = new_X, new_y
else:
X, y = np.concatenate((X, new_X)), np.concatenate((y, new_y))
X = X.astype(np.float32)
def my_model(x, y):
y = slim.one_hot_encoding(y, n_class)
with tf.name_scope(None, 'MyOp', [x]) as scope:
net = slim.stack(x, slim.fully_connected, [30 for _ in range(5)], activation_fn=tf.nn.relu, scope=scope)
logit = slim.fully_connected(net, n_class, activation_fn=None, scope=scope)
prob = slim.softmax(logit, scope='prob')
loss = slim.losses.softmax_cross_entropy(logit, y, scope='loss')
learning_rate = tf.train.exponential_decay(0.1, slim.get_global_step(), 4, 0.9994, staircase=True)
train_op = slim.optimize_loss(loss, slim.get_global_step(), learning_rate=learning_rate, optimizer='SGD')
return {'class': tf.cast(tf.argmax(prob, 1), tf.uint8), 'prob': prob}, loss, train_op
class MyMonitor(learn.monitors.EveryN):
def begin(self, max_steps):
super(MyMonitor, self).begin(max_steps)
self.variables = [t.name for t in slim.get_variables(scope='MyOp')]
self.figure = plt.figure(figsize=(4, 4))
self.cm_scatter = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
self.x_min, self.x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
self.y_min, self.y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
self.linewidth = min(self.x_max - self.x_min, self.y_max - self.y_min) / 200
self.xx, self.yy = np.meshgrid(np.arange(self.x_min, self.x_max, self.linewidth), np.arange(self.y_min, self.y_max, self.linewidth))
self.xx, self.yy = self.xx.astype(np.float32), self.yy.astype(np.float32)
self.grid = np.c_[self.xx.ravel(), self.yy.ravel()]
def end(self):
super(MyMonitor, self).end()
def every_n_step_begin(self, step):
return self.variables + ['loss/value:0']
def every_n_step_end(self, step, outputs):
print('Step {0:0>5} - loss: {1:.5f}'.format(step, outputs['loss/value:0']))
self.figure.clf()
plt.xlim(self.x_min, self.x_max)
plt.ylim(self.y_min, self.y_max)
plt.xticks(())
plt.yticks(())
logit = self.grid
n_layer = len(self.variables) // 2
for i in range(n_layer):
w, b = self.variables[i * 2], self.variables[i * 2 + 1]
logit = logit.dot(outputs[w]) + outputs[b]
if i < n_layer - 1:
logit = self.relu(logit)
else:
prob = self.softmax(logit)
prob = prob.reshape([-1, 3])
plt.scatter(self.xx.ravel(), self.yy.ravel(), c=prob, marker='.', alpha=0.8, linewidths=self.linewidth)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=self.cm_scatter)
self.figure.canvas.draw()
def relu(self, x):
x[x < 0] = 0
return x
def softmax(self, x):
e = np.nan_to_num(np.exp(x))
sum = e.sum(axis=1)
sum = np.repeat(sum.reshape([-1, 1]), 3, axis=1)
return e / sum
classifier = learn.Estimator(model_fn=my_model, model_dir='/tmp/my_model/multi_layer_perceptron')
classifier.fit(x=X, y=y, steps=n_step, batch_size=128, monitors=[MyMonitor(every_n_steps=n_step // 100, first_n_steps=0)] + learn.monitors.get_default_monitors(save_summary_steps=n_step // 100))
興味が湧いて調べてみたい場合のキーワード
- 確率的勾配降下法(SGD)をソフトマックス関数(Softmax)と交差エントロピー誤差(Cross Entropy Loss)で学習しているところはロジスティック回帰と変わりません。
- 学習率減衰(Learning Rate Decay)を利用しています。減衰率は各ステップごとに0.9994ですが、同一エポック内(今回は4ステップ)では学習率が変わらないよう(staircase=True)にしています。
- slim.stackは繰り返し用の機能で第2引数の関数に対して、第3引数の配列の値を順次適用していきます。第4引数以下は第2引数の関数実行時に毎回渡されます。似たようなものにslim.repeatがあります。
- slim.one_hot_encodingは[1, 0, 2]といった配列を、[[0, 1, 0], [1, 0, 0], [0, 0, 1]]のような形式の行列に変換します。
まとめ
初学者向けに、とりあえずコードを動かして何か動作する様子を見て興味を持ってもらうことを目的に記事を書きましたが、どうでしょうか?
コードが長いなと思うかもしれませんが、MyMonitorクラスはデモで描画するためのものなので、実質的に必要な部分はかなり短いんじゃないかなと思います。
サンプルコードを実行してみてディープラーニングに興味を持つ人が増えてくれると嬉しいです。そして、ディープラーニングやるならTensorFlowも使ってみてくださいね。