量子コンピュータでRSA暗号を解くのに必要な物は？

はじめに

量子コンピュータで、Shorのアルゴリズムを用いると、RSAの離散対数問題を位数推定という方法で求解できるのでは？というテーマはこちらで扱いました。

一方で、Shorのアルゴリズムは、
「理想的な量子コンピュータなら～～」のLong-termと呼ばれる部類のアルゴリズムですので、、
量子コンピュータでRSAを解くというのは、まだ人類未踏の領域でございます。

で、難しい。以上！と言ってもいいのですが、、
人類が何を手に入れたら量子コンピュータでRSAを解くことができるのか、
をまとめてみようというのが本稿のモチベーションです。

本稿は、下記の1.1 Our contributions and a summary of our resultsを参考に議論を進めます。

著者は産業界の１エンジニアであり、研究者でも専門家でも無いので、
間違っていたらごめんなさい。。ぜひ、コメントいただければと。。

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

大切にしたいこと

本論文¹著者のCraig Gidney氏は、下記にてActual Goalを次のように語っています。

NOT the goal: Reduce the time until RSA is broken

「量子コンピュータで早くRSAを破りたい！」とか「それを煽る！」とかではなく。

Actual goal: Understand how long until RSA is broken
Replacing internet cryptosystems is a lot of work!
How quickly dose that work need to get done?
If the estimate is going to change, we want to know that while we can react.

現実問題として、インターネット上の暗号システムの置き換えには10年単位の時間を要する。
RSAが破られるまでの見積もりも日々変化するし、だから、人類はそれを正しく理解したい。

目的は「壊す・煽る」ではなく、「正しく理解」することである。
論文著者のこの精神に強く共感し、本稿でもこの精神を大切にしたいと思います。

RSA 2048bitを解くのに必要なモノ

引用論文¹のタイトル通り、20 million noisy qubits ですね。

で、結論を先に示すと、

• エラーレートが、$\color{red}{0.1％}$の量子系で、$\color{red}{23 \times 10^{6}}$(23M量子ビット）が必要です。

これがどれだけの規模かというと、

• Google²やIBM³が約10年後の2030年までに目指す量子ビットが、1M量子ビットです。

よって、

• RSA2048を解くには、その2030年目標の23倍の物理量子ビットが必要です。加えて、、
• 現時点での一般的なエラーレートは約1%⁴ですが、10倍の精度の約0.1% が必要です。

つまり、

現状の10倍の精度（エラーレート）の量子系にて、GoogleやIBMの2030年目標の23倍の量子ビットが用意できれば、RSA2048を解くことができる「かもしれない」というお話でした。

正直、現状では、「無理では…」というのが私の感想で、

• 量子コンピュータが出てきたから、すぐに、HTTPSが危険になるかも。　とか
• 暗号資産の安全性が脅かされるから、すぐに、現金化せねば～

的なことは無く、離散対数問題を安全性の根拠するRSAもしばらく安全では？といった感覚です。
一方で、

• なぜそんなに、膨大な数の物理量子ビットが必要になるのか？

そのロジックを理解しておくことは重要な気がします。
そのロジックが崩れるような技術革新が起きれば、「しばらくは安全」が崩れてしまうので、

ということで、なぜそんな膨大な物理量子ビットが必要になるのか？の議論を進めていきましょう。

「膨大な」を正しく理解する

「膨大な」がどの様に膨大なのかを議論していきましょう。
その為に、本論文¹のTable.1のここらへんから数字を拾わせて頂き、議論を進めましょう。

で、少し整理するとこんな感じです。

	(ours)2019に記載の計算式	RSA 1024	RSA 2048	RSA 3072
Abstract Qubits5	$3n+0.002nlog(n)$	3,092	6,189	9,287
Measurement Depth6	$500n^2+n^2log(n)$	534,773,760	2,143,289,344	4,827,921,423

数字を拾ってみると、

• RSA2048を解くのに必要な論理量子ビット数は、意外に少なく、$6K$論理量子ビット
• 一方で、量子回路の深さが果てしなく深く⁷、、、$2.1 \times 10^{10}$

つまり、「膨大」 の正体は、論理量子ビット数ではなく、量子回路の深さと理解することができます。

量子回路が深いとどうなるか？

単一のゲートのエラー発生率が低くても、それを繰り返すと系としてのエラー発生率は徐々に増大します。
イメージ的には、信頼性0.9の処理があり、

• ゲート1つを通過しただけでは、$90％$は正常に処理ができますが
• ゲート4つを通過後は、$0.9^4 = 66％$となります。そして、
• ゲート8つを通過すると、$0.9^8 = 43％$となり、半分以上間違える。

という様に、深い回路を作りたい場合には、単一のゲートのエラーレートを大きく下げる必要があります。
一方で、本論文¹の議論では、前提とする、単一物理ゲートのエラーレートは、0.1％ を想定しています。

どうやって、エラーレート$0.1％$の物理系で、$2.1 \times 10^{10}$段のゲート測定を行うのでしょうか？

ノイジーな量子ビットから、きれいな１ビットをつくる

誤り訂正符号上でのTゲート適用を考える

エラーレート$0.1％$は高精度に見えますが、$2.1 \times 10^{10}$段の測定深度を要する処理の前においては、ノイズが大きく、このままでは回路を構成することが出来ません。
そこで、この$0.1％$の物理量子ビットを束ねて、きれいな（高精度な）１ビットを作ります。

どうやって作るか？ですが、

といった様に、物理量子ビットを複数用いて、誤りに強い量子ビットを作ります。
量子ビットに対する演算は、下記でも見たように、$H,T,CNOT$により完全系をなすので、論理量子ビット上でも、$H,T,CNOT$を使いたいのですが、実を言うと、論理量子ビット上では論理$T$ゲートを使うことが出来ません。

理由としては、論理$T$ゲートがクリフォード演算子では無いから。なのですが、今はアウトラインだけを追いかけたいので詳細は省略します。
で、どうするかというと、誤り訂正符号によりエラーから保護された論理状態に対して、ゲートテレポーテーションを用いることで、間接的に$T$ゲートを作用させ$T$操作を実現します。

純度の高いTをどう準備するか？

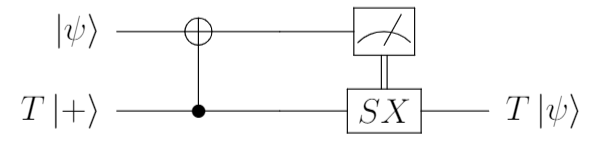
ゲートテレポーテーションでは、$T$ゲートを準備する代わりに、$T$が作用した状態を準備します。

\newcommand{\ket}[1]{\left| #1 \right\rangle}

• $\ket{\psi}$(上段)は誤り訂正符号にてエラー保護済みですが、$T\ket{+}$(下段)は、物理状態として準備します
• この$T\ket{+}$は、こういった簡単な回路で準備も可能ですが、この$T$にノイズがあったらどうでしょうか？
• せっかく、誤り訂正符号で守り抜いたきれいな状態も、汚い$T$によってノイズが混じってしまいます。

蒸留により高純度なTをつくる（魔法状態蒸留）

誤り訂正符号で守り抜いてきた論理状態に対して、適用しても害がないレベルに磨き上げられた$T$状態がほしいのですが、それを手に入れる手法が、魔法状態蒸留です。詳細は割愛しますが、ゲート適用と間接測定を繰り返し、高純度な$T$を作り上げることができるのですが、回路としてはこんなになります。。

• Magic State Distillation

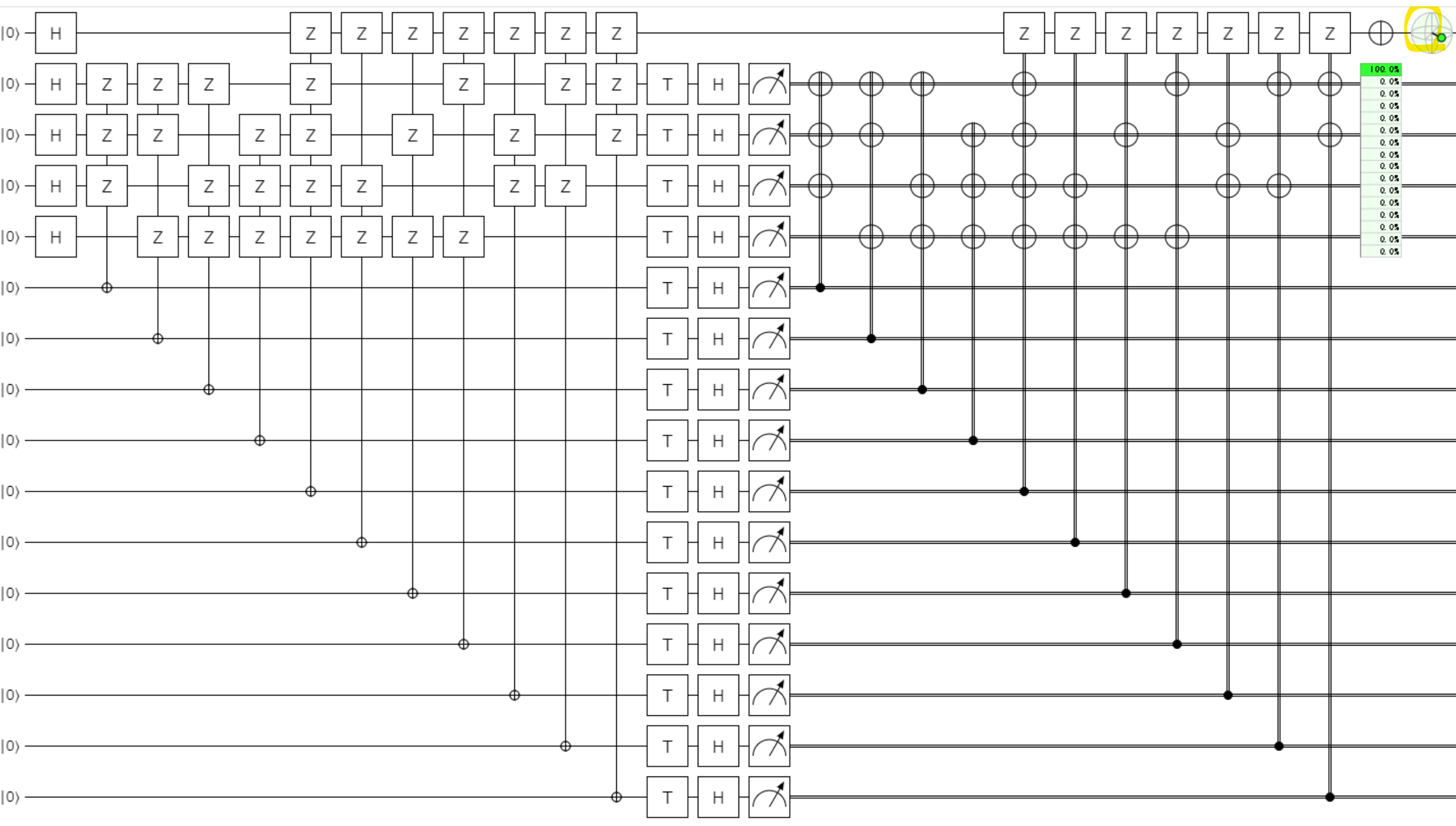
きれいなビットで計算する方法をまとめると

演算は誤り訂正符号のエラー保護下で進めるのだが、クリフォード演算でない$T$が論理状態には適用できないので、事前にこの高純度の$T$状態を大量に準備しておいて、$T$ゲートを掛けたいタイミングでは、ゲートテレポーテーションを使って$T$の効果を量子状態に反映する。手間がかかります。。
実際に、本論文¹においても、

When factoring an n = 2048 bit RSA integer we are using a board of 226 · 63 logical qubits.
Approximately 25% of these qubits are being used for distillation, which we already accounted
for, and so we do not count them in this calculation.

といった記述があり、全量子ビットの約25%が、この魔法状態の蒸留の為に利用されているようです。
（詳細は著者も理解が追いつかないのですが、雰囲気として、すごいオーバヘッドを感じました。。）

量子誤り訂正の厳しさ

冒頭に見たようにRSA2048を解くためには、$2.1 \times 10^{10}$の測定深度が必要ですが、先程の信頼性・故障率の議論と同様に、これを実現するには、１論理量子ビットのエラーレートを、$10^{-14}$程度まで抑え込む必要があるようです。
では、物理何ビットを用いれば、この$10^{-14}$の１論理量子ビットを得ることができるのでしょうか？
表面符号⁸における物理誤り率を論理誤り率に換算する式については下記⁹、

にて、近似値が示されており、

P_{Logical} = 0.1(100 \times P_{physical})^{(d+1)/2}

となるようです。
この数式は何を言っているか？というと、

• 所望の論理誤り率は、 $P_{Logical} =10^{-14}$
• 利用する物理系の誤り率は、$P_{physical} = 0.1％ = 10^{-4}$

ですので、下記となり

10^{-14} \gt 0.1(100 \times 10^{-4})^{(d+1)/2}

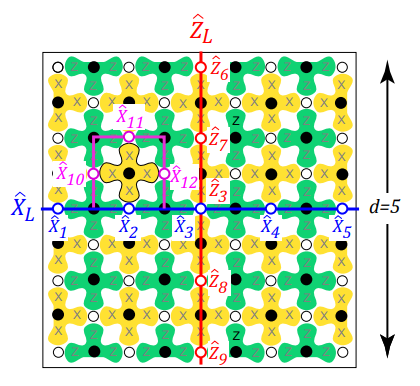
これを満たすようにdを奇数で決めると、$d=27$となり、この$d$は何を表すかというと、下記の様に表面符号⁸上の符号距離を意味しており、dに対して、この表面符号⁸を構成する物理ビットは、

2(d+1)^2 

で計算できます。つまり、$d=27$のときに必要な物理ビット数は、$2(27+1)^2=1568$となります。
つまり、1568物理量子ビットを用いて、１論理量子ビットを構成する必要があるのです。
（以下は、$d=5$のときの図で、白・黒の◯が量子ビットを表しています）

エラーレート=1%で考える

今までの議論では、単一物理量子ビットのエラーレートを0.1%で考えてきましたが、現有する物理系の一般的なエラーレート1%でこの式を考えてみると、悲しき事実がわかります。

P_{Logical} = 0.1(100 \times P_{physical})^{(d+1)/2}

$P_{physical}=1％=10^{-2}$を代入すると、

P_{Logical} = 0.1(100 \times 0.01)^{(d+1)/2} = 0.1(1)^{(d+1)/2}

$1^{(d+1)/2}$は何を意味しているでしょうか？そうです、1は何回掛けても1ですので、エラーレート1%時は、dの符号距離をいくら大きくし、物理量子ビットを増やしても、論理誤り率は改善しないのです。

つまり、RSAを解くには、Long-termアルゴリズムを使うには、

人類は、膨大な量子ビットを、物理エラーレートを1%未満で実現する量子系を手に入れるしかないのです。Long-term厳しいです。。

今までの議論をまとめる

• RSAを量子コンピュータで解くためには、深い回路が必要
• 深さを得ようとすると、単一エラーレートを低く抑え込む必要があり
• 表面符号等を用いた上で、演算Tは魔法状態蒸留した論理Tをゲートテレポーテーションする

この背景で、膨大な物理量子ビットが必要になる。
「膨大」の意味を細かめに見ていきましたが、やはり、RSAが量子コンピュータで解かれる日はまだ来そうにありません。

安心していいのか？（ここからは思考実験）

以下の議論は、一個人の思考実験ですので、正確性を大きく欠くと思います。
「思考実験なのだな」とお付き合いいただければ幸いです。

「すぐに」RSAが量子コンピュータで解かれる事はないと思います。
ただ、事実として、こういった話があります。

何がすごいかというと、RSAのビット数$n$に対して、

2016年の手法は、$n^3$オーダだった回路の深さが、2019年の手法では、$\color{red}{n^2}$オーダに改善

これは、研究者ではない１エンジニアの感想に過ぎませんが、技術革新の匂いを感じます。

歴代の改善を並べてみる

各手法が前提とする条件もバラバラなので、この議論にどれだけの意味があるかは不明です。

ですが、歴代の手法がどれだけの改善を成し遂げてきたのか？には興味があります。
幸いにもこの論文¹のB2. Entriesにて歴代の手法を紹介する論文がリスト化されていたので、各手法¹⁰¹¹¹²がどれだけの物理量子ビットを要求するか？をプロットしてみました。
こう見てみると、

• 2010年には、65億物理ビットが必要とされていたRSAの解読も
• 2019年には、23百万物理ビットまで減少しており、技術は革新を続けています。

マシンメーカ各社のロードマップと見比べる

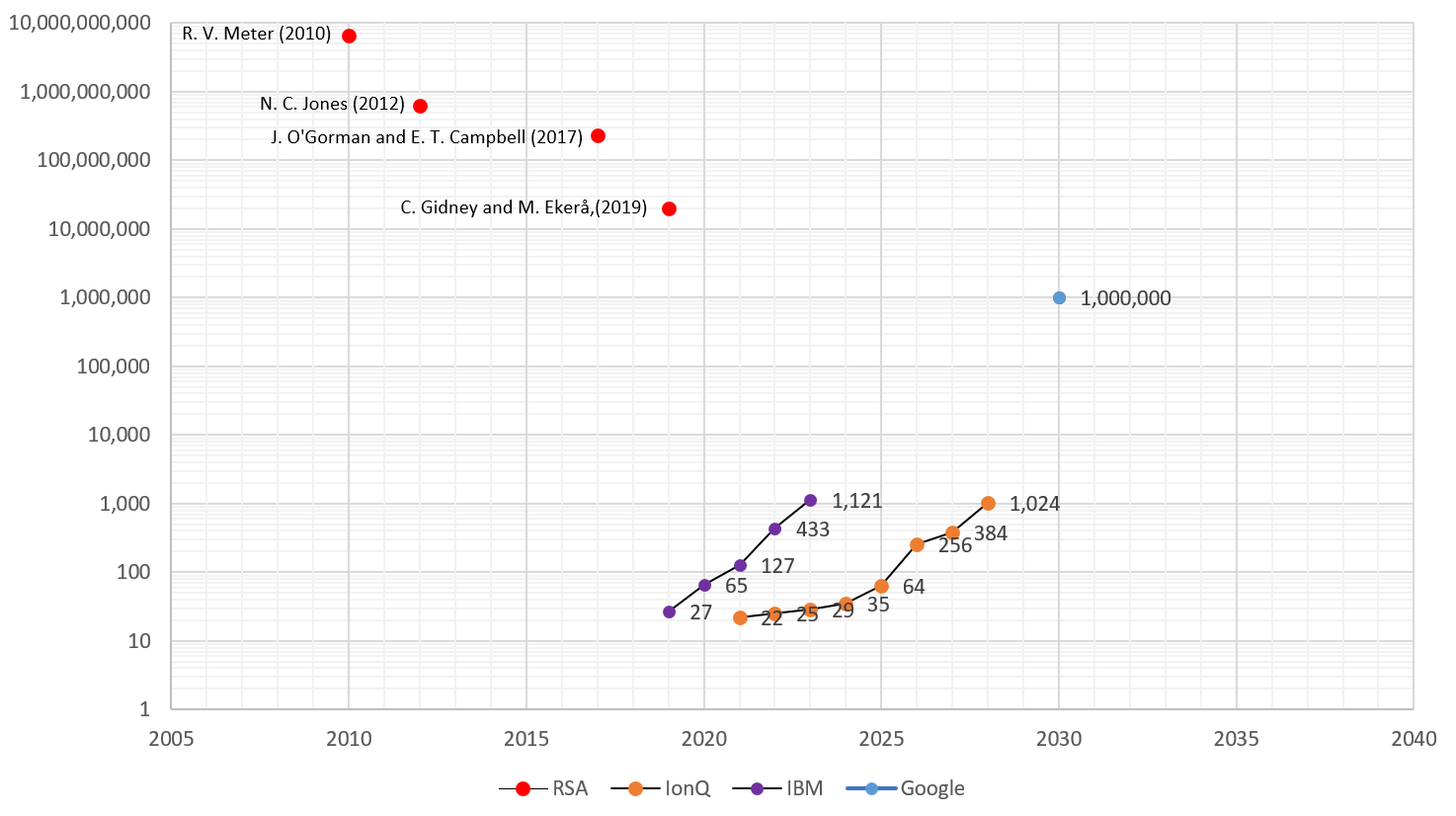
量子ビット拡大のロードマップを発表しているマシンメーカ（Google、IBM¹³、IonQ¹⁴）の情報をマッピングしてみるとこんな構図となります。

こうやって見てみると、

• 現時点では、RSAを量子コンピュータで解くというのは、ほぼ「無理ゲー」です。
• ただ、「RSAを解くアルゴリズム」、「量子コンピュータメーカ」は双方、技術を磨き続けます
• そうすると、いつか、RSAが量子コンピュータで解かれるXデーが到来する。（かもしれません）

我々はどうすべきなのだろう？

冒頭の議論に戻るのですが、

Actual goal: Understand how long until RSA is broken
Replacing internet cryptosystems is a lot of work!
How quickly dose that work need to get done?
If the estimate is going to change, we want to know that while we can react.

現実問題として、インターネット上の暗号システムの置き換えには10年単位の時間を要する。
RSAが破られるまでの見積もりも日々変化するし、だから、人類はそれを正しく理解したい。

これに尽きるのかもしれません。

• RSAが破られるまでの見積もりも日々変わる（下図の、赤い矢印の力）
• 量子コンピュータのハードウェアも日々成長する（下図の、青い矢印の力）

ただ、双方ともに研究者が最新情報を発信し続けてくれています。
我々はその最新情報にきちんと耳を傾け、（もしかしたら来てしまう）Xデーに向けて、10年単位の時間を要する暗号刷新という大事業を進めるのか？も判断しながら、PQC(post quantum cryptography)時代を無事に迎えられるよう、傾聴と行動の努力が求められるのかもしれません。

まとめ

研究者でもない１エンジニアの大変長い記事となってしまいましたが、いかがだったでしょうか？
そんな背景で、派手に間違っている可能性もありますのでｗｗ
ぜひ、専門家の発信する情報に耳を傾けていただければ幸いです。

※本稿の内容は個人の見解であり、所属する組織の公式見解ではありません。

1. Craig Gidney and Martin Eker˚a.
   How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits, 2021 ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶ ↩⁷ ↩⁸ ↩⁹

2. https://ia.acs.org.au/article/2021/google-is-building-a-1-million-qubit-quantum-computer.html ↩

3. https://fortune.com/2020/09/15/ibm-quantum-computer-1-million-qubits-by-2030/ ↩

4. A. Rossi, P.G. Baity, V.M. Schäfer, M. Weides.
   Quantum computing hardware in the cloud: Should a computational chemist care?, 2021を参考にさせていただいています。超伝導でも規模が小さいものやイオントラップ型は、量子ビットサイズに対して、Quantum Volumeも大きくシングルビッドのフィディリティも0.1%程度のものも存在しますが、規模を大きくしようとすると、現状のシングルビットフィディリティはやはり、今もまだ、1%程度ではないか。と考えています。 ↩

5. 論文¹では、The number of logical qubits used in the abstract circuit model. Ignores qubits used for distillation and routing.と記載があり、論理量子ビット数を解釈しました。 ↩

6. 論文¹では、The length of the longest chain of dependent measurements, which determines the reaction limited runtime of an algorithm. These numbers are not adjusted to account for the chance of retrying.と記載があり、測定深度（ゲートの深さ）と解釈しました。誤解があればコメントいただけるとたすかります。 ↩

7. 必要な量子ビット数23Mに対して、測定深度が21Bと量子ビット数を上回っていたので、違和感を感じたのですが、論文¹では、Uncomputation等のテクニックにより量子ビットの再利用が行われている記述があり、23Mの量子ビットを再利用しながら、計算を都度進めていくと最終的な測定深度は、その量子ビットサイズを遥かに上回る深さとなる。と理解していますが、誤解もありそうなのでコメント頂けますと幸いです。 ↩

8. Austin G. Fowler, Matteo Mariantoni, John M. Martinis, Andrew N. Cleland.
   Surface codes: Towards practical large-scale quantum computation, 2012 ↩ ↩² ↩³

9. Austin G. Fowler, Craig Gidney.
   Low overhead quantum computation using lattice surgery, 2018 ↩

10. R. Van Meter, T. D. Ladd, A. G. Fowler, and Y. Yamamoto.
    Distributed Quantum Computation Architecture Using Semiconductor Nanophotonics, 2010 ↩

11. N. Cody Jones, Rodney Van Meter, Austin G. Fowler, Peter L. McMahon, Jungsang Kim, Thaddeus D. Ladd, Yoshihisa Yamamoto.
    Layered architecture for quantum computing, 2012 ↩

12. Joe O'Gorman, Earl T. Campbell.
    Quantum computation with realistic magic state factories, 2017 ↩

13. IBM’s roadmap for scaling quantum technology ↩

14. Scaling IonQ's Quantum Computers: The Roadmap ↩