はじめに

アドベントカレンダも12日目となりました。本日は、Groverのアルゴリズムです。

複数の選択肢の中から、所望の状態を見つけ出すGroverのアルゴリズム。
所望の状態とは、データそのもの、パターンや条件でも良いです。

100個のデータ"77"というデータを見つけたい　→　"77"というデータそのもの
選択肢の中からルールや条件に適合するものを見つけたい　→　その条件やパターン

探索アルゴリズムであるGroverについて丁寧に書いてみたいと思います。
なお、誤り等あれば、ぜひコメント頂ければ幸いです。

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

なお、本記事は、下記を再編集したもので、既読の方には重複の内容となります。

Grover Search①：Oracleを丁寧に説明してみる
 Grover Search②：Oracle work bit
Grover Search③：3-bit Grover Search

$$
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \ #3 & #4 \end{bmatrix}}
$$

Groverのアルゴリズム

まずは、Groverのアルゴリズムの概略を説明します。¹

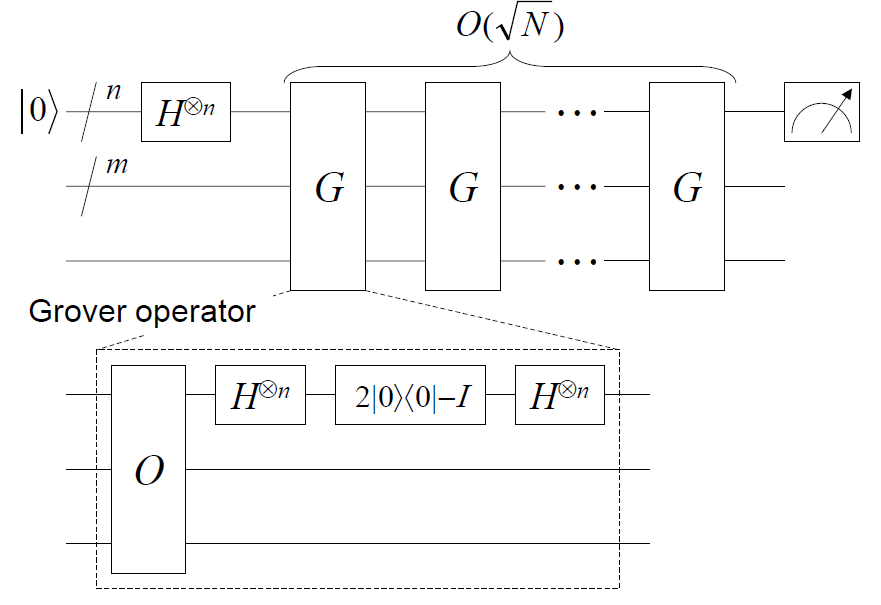
#	手順	図との対応
①	全ビットを$H$ゲートにより均等な重ね合わせ状態にする。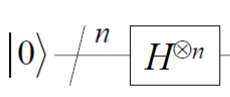
②	OracleとIAMで構成するGrover Operatorを、√N回適用する。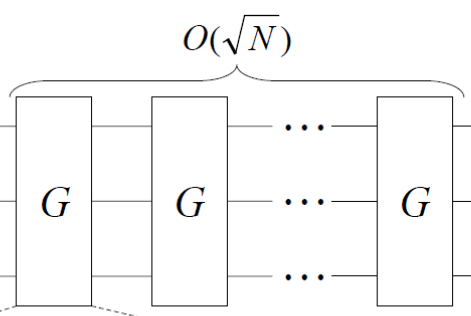
	②-1 Oracle：探索対象の確率振幅だけを、マイナスにする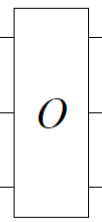
	②-1 IAM ：マイナスの確率振幅を増幅し、見つけやすくする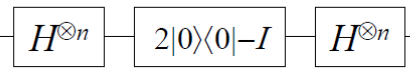
③	繰り返し後に量子ビットを測定すると、探索対象が現れる

2bit Grover

よりシンプルに説明するために、2ビットのGrover Searchを考えます。
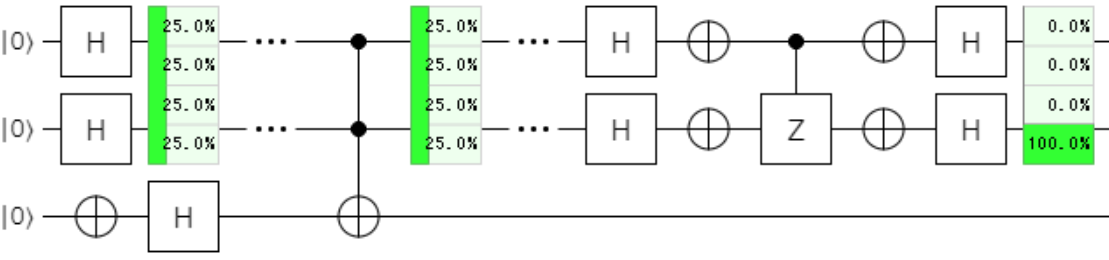
今回は、下記の回路を作成していきたいと思います

2bit GroverをQuirkで開く

①：Hゲートで均等重ね合わせ

２ビットの均等な重ね合わせを作ります。
確率振幅の２乗が、そのビットパターンの観測確率だったので、下記は$1/4$の均等な確率で、00,01,10,11を観測します。

\ket{00} \xrightarrow{H_1,H_2} 
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)

②：Grover Operatorを√N回繰返す

今回は、適用回数１回ですが、、

データ数Nに対して√Nのペースで Operatorの適用回数が増えます。
データ数の増分に対して、このGrover Operatorの適用回数に√が掛かる。

これが、古典での探索と比較した場合に、Grover Searchが高速であると言われる所以です。
では、Grover Operatorの中身を見ていきましょう。

②-1：Oracleを適用する

Oracleとはなにか

Oracleとは何でしょうか？Wikipediaによると、「神託（神のお告げ）」ですね。
何をするかというと、神のように正解を言い当てる機能を担います。

冒頭で説明したとおり、Oracleに探索対象データを与えると正解を言い当てます
そして、その正解に対応する、量子状態の確率振幅にマイナスを付与します

「これが正解」とい言い当てる機能が実装出来れば、それはOracleとして機能できます
データの検索で0～100に対して、"77"が正解であれば、その時にだけマイナスを付与する

ここで、出てくる疑問として、"77"という正解を知っている必要がある。
これって、「答えをカンニングしてるやん」
そうです。「神様、答えをカンニングしている疑惑」ですｗ

ですが、、

正解を知らなくてもOracleは実装できる

（誤解を恐れずにいうと）「正解そのものを知らなくても良いのです」
※これからはたとえ話になりますが、例えば

子供に人気の食べ物で、黄色くて、ケチャップをかけて、スプーンで食べる。
原材料は、卵、鶏肉、たまねぎ、ご飯、しお、胡椒、サラダ油
ご飯の上に、卵を加熱したものをかけた食べ物
上記条件を満たすものが正解なので、符号をマイナスにします

上記のように、「正解を言い当て」そのときに「マイナスを付与する」機能を量子回路上で実装できるのであれば、それはOracleになります。²

つまり、正解が「オムライス」であることを知らずとも、
その特徴や条件を書き下すことができればOracleを実装することができます。（と理解しています）

具体例

こちらの記事では、最適な出店パターンの探索にGrover Searchを使っています。
データ検索ではなく、出店に求められる条件や特性をOracleとして実装します。

ただ、今回は簡単のために数字を探します

今回の問題設定では、探索の分母の数は４となります。0～3の中から3を探します。

探索対象	量子ビット上での状態表現	Oracleが正解とするもの
0	$\ket{00}$
1	$\ket{01}$
2	$\ket{10}$
3	$\ket{11}$	★対象★ この確率振幅をマイナスに

Oracleの構成方法

一般的には、**Oracle Work bit (Work Space)**というマーキング用の補助ビットを用いるのですが、今回は簡単にするために、$CtrlZ$ゲートを使います。
Oracleでは、均等な重ね合わせに対して、$\ket{11}$の位相（符号）をマイナスに反転したい
つまり、

\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{Oracle}} 
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}\color{red}{-1}\ket{11}
\right)

これをどう構成すれば良いでしょうか？
Zゲートは

\displaylines{
Z\ket{0} = \ket{0}
\\
Z\ket{1} = \color{red}{-1}\ket{1}
}

ですので、マイナスを付けるのに使えそうです。
そして、今対象は２量子系ですので、制御付きＺ（$ctrlZ$）を使ってみたらどうでしょう。

\displaylines{
CZ\ket{00} = \ket{00}
\\
CZ\ket{01} = \ket{01}
\\
CZ\ket{10} = \ket{10}
\\
CZ\ket{11} = \color{red}{-1}\ket{11}
}

なので、今回のOracleは、制御付きＺ（$ctrlZ$）で良さそうです。
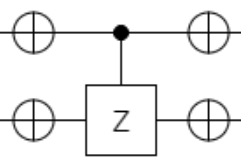
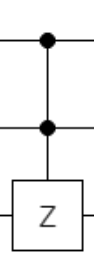
つまり、下記の回路の赤い部分になります。

つまり、

\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{CZ_{oracle}}} 
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}\color{red}{-1}\ket{11}
\right)

マーキング（位相反転）の確認

説明に利用しているQuirkの、Probabilty Display（確率表示）には、符号（位相）は表現されないので、別の可視化（Amplitude Display）で位相も確認しておきましょう。

Quirkで位相反転を確認する

マウスオーバすると、$CZ$の前後で$\ket{11}$の位相（符号）だけが反転していますね。

②-2：IAMで、位相がマイナスの確率振幅を増幅する

上記でも確認したとおり、

Oracleはターゲットとなる量子状態に対して、位相（符号）を反転するだけです。
確率振幅は増幅しないので、Oracleを適用したあとの量子状態を観測しても測定により均等な重ね合わせとなります。
つまり、Oracleを適用後でも、00、01、10、11の観測確率はそれぞれ、$1/4$のままです。

これでは、所望の11を見つけることができないので、観測したときに所望の量子状態を観測しやすくするために（目立たせるために）位相（符号）がマイナスの量子状態の観測確率（確率振幅）を増幅します。

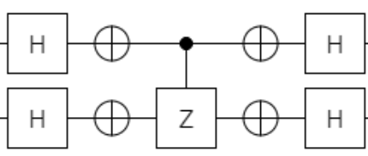
そして、その振幅増幅には、下記回路を使います。

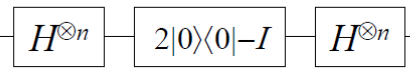
今回の作成する回路でいうと、

です。

$H^{\otimes n}$は、$H$ゲートをnビットに対し適用するという意味なので上記の通り２ビットに$H$ゲートを適用しておきます。
少し確認したいのは、$2\ketbra{0}{0}-I$　のPhase Shift Operatorです。

Phase Shift Operatorの確認

今回は、2bit Groverですので、³

\displaylines{
-(2\ket{00}\bra{00} - I) = -2 
\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}
\begin{bmatrix} 1 & 0 & 0 & 0 \end{bmatrix}
+I
\\
= 
\begin{bmatrix}
 -2 & 0 & 0 & 0 \\
 0 & 0 & 0 & 0 \\
 0 & 0 & 0 & 0 \\
 0 & 0 & 0 & 0 \\
\end{bmatrix}
+
\begin{bmatrix}
 1 & 0 & 0 & 0 \\
 0 & 1 & 0 & 0 \\
 0 & 0 & 1 & 0 \\
 0 & 0 & 0 & 1 \\
\end{bmatrix}
=
\begin{bmatrix}
 \color{red}{-1} & 0 & 0 & 0 \\
 0 & 1 & 0 & 0 \\
 0 & 0 & 1 & 0 \\
 0 & 0 & 0 & 1 \\
\end{bmatrix}
}

となり、

入力が$\ket{00}$のときに、位相を-1にする演算子ができました。

一方で、

入力が$\ket{11}$のときに、位相を-1にする演算子が、$CtrlZ$ですので、

CtrlZ = 
\begin{bmatrix}
 1 & 0 & 0 & 0 \\
 0 & 1 & 0 & 0 \\
 0 & 0 & 1 & 0 \\
 0 & 0 & 0 & \color{red}{-1} 
\end{bmatrix}

つまり、

$CtrlZ$に入力する前に、２ビットとも$X$で反転させ入力し、
処理が終わったあと$X$で元に戻すような演算子が必要となります。

それが、下記回路で表現されています。
実際に、下記回路のテンソル積を計算すると上記行列と一致します。

IAM(Inversion About Mean)でなぜ振幅増幅するか

詳細は、下記サイトの解説を参照ください。リンクさせていただきます。

概略だけ記載すると、

全量子状態の確率振幅の平均値に対して折り返す。
この操作を行うと、Oracleにより負にマーキングされた量子状態の確率振幅だけが、＋／－／＋と揺さぶられ、この折返しにより、その確率振幅が１に近い状態に近づきます。

といった感じの処理になります。

③：Grover Operatorを繰り返したあと測定する

最後です。
Grover Operatorにより、探したかった3に対応する$\ket{11}$の確率振幅が１に近い状態になっています。
この状態まで持ち込めば、測定により１に近い確率で、所望の$\ket{11}$を観測することができます。

ここまでのまとめ

Grover Searchについて、主にOracleを詳しく説明しました。

Oracleは、「探し出すもの」が表現できれば、データでも良いですし、条件でも良いです。
Oracleにより、探し出すものの確率振幅にマークをつけます（確率振幅をマイナスにする）
次に、IAMにより、確率振幅を平均値に対して折り返すことで、振幅増幅をします。
そして、これらを繰り返して、観測に都合が良いタイミングになったら観測して結果をえる。

こんな流れでした。で、活用に向けたポイントとしては、

データの表現の仕方と、Oracleの設計にコツがあると考えています。
一方で、IAMは形が決まってしまっているので、パターン化が可能かと。

よって、賢いデータ表現とOracleをどう設計するか？が活用のポイントになると思います。

他のデータを探すには？

これまでは、3(11)を探していましたが、0(00)、1(01)、2(10)についてもOracleを考えてみましょう。
他のパターンを表現するためのOracleも考えてみましょう。
諸事情あり、説明順を下記とさせていただきます。

$\ket{10}$を探す
$\ket{01}$を探す
$\ket{00}$を探す（Oracle work bitをつかう）

|10>を探す

均等な重ね合わせに対して、$\ket{10}$の位相を反転（マイナスをつければ）実現出来ます。
どうやれば良いでしょうか？

\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{\color{red}{Oracle}}} 
\frac{1}{2}
\left(
\ket{00}+\ket{01}\color{red}{-1}\ket{10}+\ket{11}
\right)

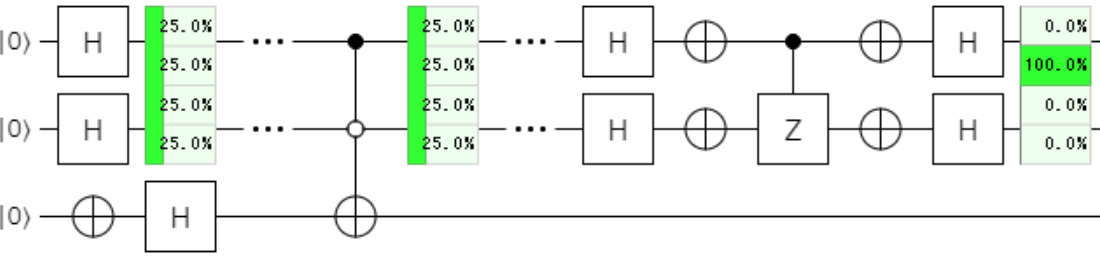
下記のように、制御ビットを反転させる白丸にすれば良いですね。
制御が$\ket{0}$だったら、標的に$Z\ket{1} = \color{red}{-1}\ket{1}$を適用し、位相を反転させる。

|01>を探す

均等な重ね合わせに対して、$\ket{01}$の位相を反転（マイナスをつければ）実現出来ます。
どうやれば良いでしょうか？

\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{\color{red}{Oracle}}} 
\frac{1}{2}
\left(
\ket{00}\color{red}{-1}\ket{01}+\ket{10}+\ket{11}
\right)

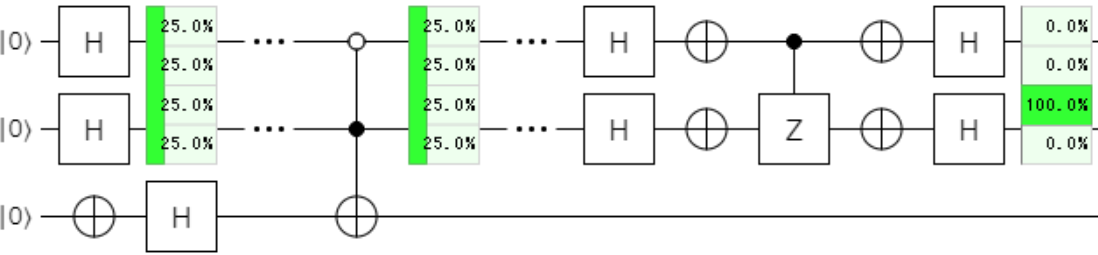
下記のように、制御ビットと標的ビットを反転させて上で、制御ビットを反転させる白丸にすれば良いですね。
制御が$\ket{0}$だったら、標的に$Z\ket{1} = \color{red}{-1}\ket{1}$を適用し、位相を反転させる。

|00>を探す

均等な重ね合わせに対して、$\ket{00}$の位相を反転（マイナスをつければ）実現出来ます。
どうやれば良いでしょうか？

\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{\color{red}{Oracle}}} 
\frac{1}{2}
\left(
\color{red}{-1}\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)

実を言うと、このパターンは$CtrlZ$では、対応出来ません。
なぜならば、

$Z$ゲートは、$Z\ket{1}=\color{red}{-1}\ket{1}$と、$\ket{1}$に対して、$\color{red}{-1}$を吐き出します。
一方で、今、位相を反転させたいのは、$\ket{00}$なので、$Z$ゲートでは位相反転が出来ないのです。

Oracle work bitを使う

どんなビットパターンだとしても、位相反転できるよう補助ビットを使った位相反転を実装しましょう。
これが、Oracle work bitです。やり方は簡単で、補助ビットを追加します。

なにが起きたかを数式で確認しておきましょう。
補助ビット側は、$HX\ket{0}=H\ket{1}=\ket{-}$ですので、

\displaylines{
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\otimes
\ket{-}_{work}
\\
=\frac{1}{2\sqrt{2}}(
\ket{000}+\ket{010}+\ket{100}+\ket{110}
-
\ket{001}-\ket{011}-\ket{101}-\ket{111}
)
}

が初期状態です。これに、Toffoli(CCX)の制御反転バージョンを適用します。
つまり、Ctrlビットが、両方とも$0$のときに、標的ビットに$X(Not)$が掛かるので、
下記となります（青が制御、赤が反転した標的）

\displaylines{
\frac{1}{2\sqrt{2}}(
\ket{\color{blue}{00}\color{red}{1}}+\ket{010}+\ket{100}+\ket{110}
-
\ket{\color{blue}{00}\color{red}{0}}-\ket{011}-\ket{101}-\ket{111}
)
\\
=
\frac{1}{2}
\left(
\color{red}{-1}\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\otimes
\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})
\\
=
\frac{1}{2}
\left(
\color{red}{-1}\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\otimes
\ket{-}_{work}
}

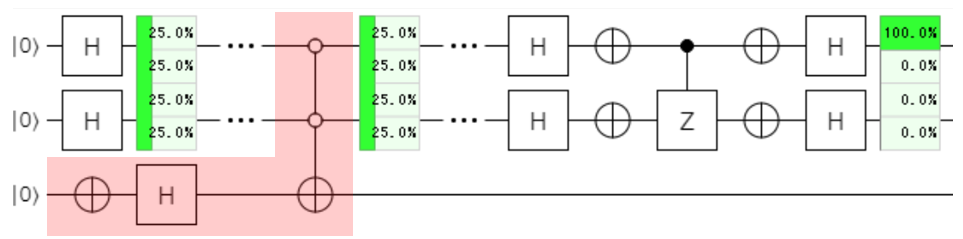
無事、$\ket{00}$の位相を反転することができました。
Oracle work bitを使ったほうが、Oracleの指定は柔軟ですが、$CtrlZ$で反転できる対象の場合は、$CtrlZ$を使うほうが回路がシンプルな気がします。

2bit Grover Searchのまとめ

Oracleを$CtrlZ$でなく、Oracle work bitを利用し実装しました。

work bitを$(\ket{0}\color{red}{-1}\ket{1})/\sqrt{2}$で準備し、この$\color{red}{-1}$をうまく使う
$CCX$ゲートで、探索対象の量子状態の相対位相をうまく反転させる。

といった、処理の流れでした。
全パターンの指定を下記に示し、まとめとさせていただきたいと思います。

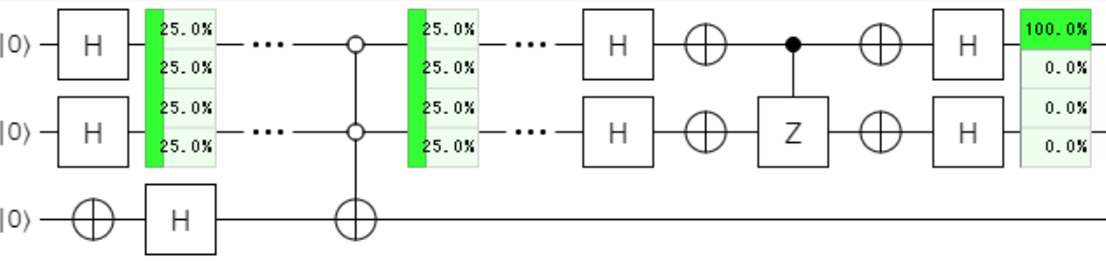
最後に3-bit Grover Search

Oracle

要領は2ビットのときと同様です。探索対象の相対位相をマイナスにマーキングすればよいので、
$\ket{111}$が探索対象であれば、下記の様に指定します。

IAM(Inversion About Mean)

こちらも、2bitの時は、

IAM_{2bit} = H^{\otimes{2}}(2\ket{00}\bra{00}-I)H^{\otimes{2}}

で、回路としては下記でした。

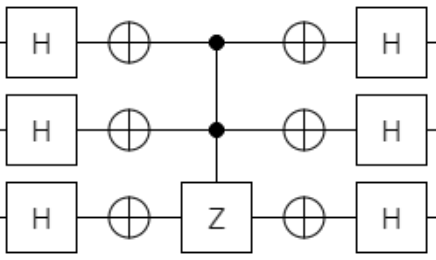
3bitになると同様の要領で、

IAM_{3bit} = H^{\otimes{3}}(2\ket{000}\bra{000}-I)H^{\otimes{3}}

となります。

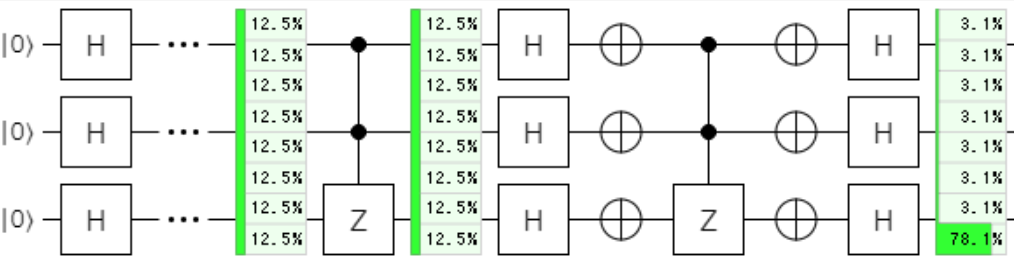
動かしてみる

Grover Operatorを１回適用

上記で構成した、Grover Operatorを１回適用してみます。

Grover operatorを１回適用@Quirk

上記ですと、探索の対象である、$\ket{111}$が測定により観測できる確率は、78%です。
ちょっと、物足りないです。
そうです。Grover Operatorの適用回数はデータ数によって変わるので、Operatorの適用回数が足りていません。
なので、足しましょう。

Grover Operatorを２回適用

Grover Operatorを２回適用してみます。

Grover Operatorを２回適用

これで、探索の対象である、$\ket{111}$が測定により観測できる確率は、94.5%です。
無事に所望の結果が得られそうです。

で、実を言うと、３回適用する（適用回数過多）だと所望の状態は観測できないのです。
詳細は、下記参照頂きたいですがいい塩梅が重要とおぼえておいていただければ幸いです。

まとめ

かなり長い記事になってしまいましたが、まとめると、

Groverのアルゴリズムの構成要素である、OracleとIAM(QAA)を説明しました。
探索の条件はOracleとして表現するので、Oracleの設計がポイントとなります。
Oracleについては
- 2-bit Groverについては、シンプルに$Ctrl-Z$ゲートを用いて構成しました。
- ただ、$Ctrl-Z$では全４パターンのOracleが表現できないので、Oracle Work bitを導入しました。
最後に、3-bit Groverを構成しました。あとは何ビットになっても考え方は一緒です。

パターンを探索するアルゴリズムなので、データ探索でも、組み合わせの探索でも、例えばSAT問題ってのも解くことができます。
具体的な計算については別記事で後日まとめてみたいと思います。

https://quantum.riken.jp/pdf/qc4.pdfより引用 ↩
実際には、こういった複雑な情報が量子回路上で表現された上で、それを判断することができるOracleを構成する必要があるので、現状の量子コンピュータではまだまだ、情報のエンコードもOracleも実装することは出来ませんが、原理的にはこういうことだと理解しています。 ↩
引用した資料の図では、$2\ket{00}\bra{00}-1$なのですが、全体の符号を逆転した$-(2\ket{00}\bra{00}-1)$でないと、計算結果が合わないので全体に、マイナスを掛けています。 ↩