はじめに
複数の選択肢の中から、所望の状態を見つけ出すGroverのアルゴリズム。
下記では説明しきれなかった、Oracle Work Bitについて説明してみたいと思います。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
$$
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \ #3 & #4 \end{bmatrix}}
$$
Oracleの構成方法(振り返り)
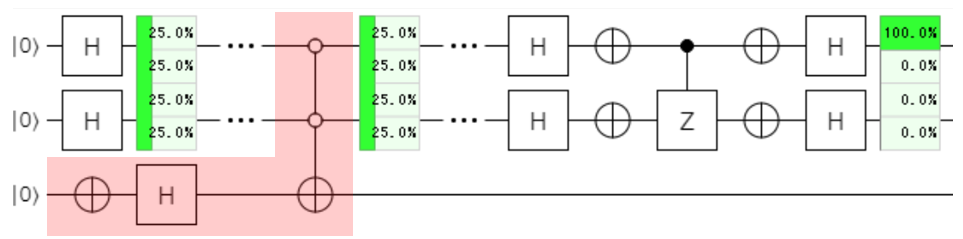
2bit Grover Search@Quirkは下記のような回路で構成でき、Oracleは赤の部分でした。
詳細は、冒頭の記事を確認いただきたいですが、均等な重ね合わせに対して、探し出したい$\ket{11}$の位相(符号)をマイナスに反転したい、つまり、
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{CZ_{oracle}}}
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}\color{red}{-1}\ket{11}
\right)
といった具合に、$\ket{11}$の位相だけを、$-1$にマーキングする目的で、$CtrlZ$を適用しています。
他のデータを探すには?
他のパターンを表現するためのOracleも考えてみましょう。
諸事情あり、説明順を下記とさせていただきます。
- $\ket{10}$を探す
- $\ket{01}$を探す
- $\ket{00}$を探す(Oracle work bitをつかう)
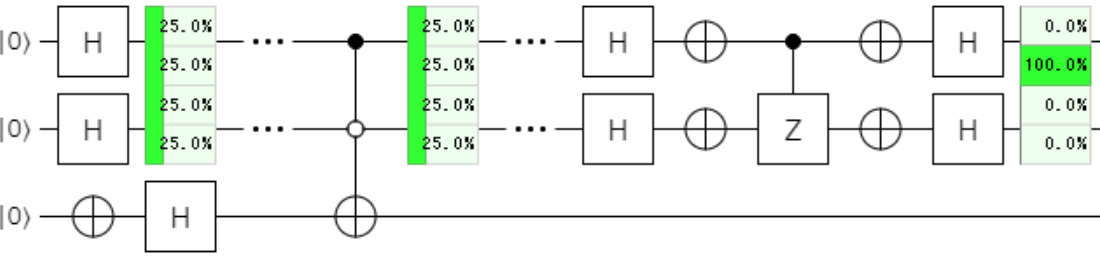
|10>を探す
均等な重ね合わせに対して、$\ket{10}$の位相を反転(マイナスをつければ)実現出来ます。
どうやれば良いでしょうか?
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{\color{red}{Oracle}}}
\frac{1}{2}
\left(
\ket{00}+\ket{01}\color{red}{-1}\ket{10}+\ket{11}
\right)
下記のように、制御ビットを反転させる白丸にすれば良いですね。
制御が$\ket{0}$だったら、標的に$Z\ket{1} = \color{red}{-1}\ket{1}$を適用し、位相を反転させる。
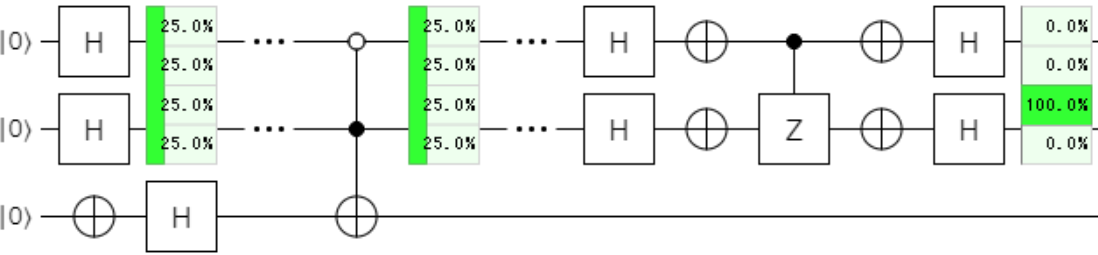
|01>を探す
均等な重ね合わせに対して、$\ket{01}$の位相を反転(マイナスをつければ)実現出来ます。
どうやれば良いでしょうか?
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{\color{red}{Oracle}}}
\frac{1}{2}
\left(
\ket{00}\color{red}{-1}\ket{01}+\ket{10}+\ket{11}
\right)
下記のように、制御ビットと標的ビットを反転させて上で、制御ビットを反転させる白丸にすれば良いですね。
制御が$\ket{0}$だったら、標的に$Z\ket{1} = \color{red}{-1}\ket{1}$を適用し、位相を反転させる。
|00>を探す
均等な重ね合わせに対して、$\ket{00}$の位相を反転(マイナスをつければ)実現出来ます。
どうやれば良いでしょうか?
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\xrightarrow{\color{red}{\color{red}{Oracle}}}
\frac{1}{2}
\left(
\color{red}{-1}\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
実を言うと、このパターンは$CtrlZ$では、対応出来ません。
なぜならば、
- $Z$ゲートは、$Z\ket{1}=\color{red}{-1}\ket{1}$と、$\ket{1}$に対して、$\color{red}{-1}$を吐き出します。
- 一方で、今、位相を反転させたいのは、$\ket{00}$なので、$Z$ゲートでは位相反転が出来ないのです。
Oracle work bitを使う
どんなビットパターンだとしても、位相反転できるよう補助ビットを使った位相反転を実装しましょう。
これが、Oracle work bitです。やり方は簡単で、補助ビットを追加します。
なにが起きたかを数式で確認しておきましょう。
補助ビット側は、$HX\ket{0}=H\ket{1}=\ket{-}$ですので、
\displaylines{
\frac{1}{2}
\left(
\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\otimes
\ket{-}_{work}
\\
=\frac{1}{2\sqrt{2}}(
\ket{000}+\ket{010}+\ket{100}+\ket{110}
-
\ket{001}-\ket{011}-\ket{101}-\ket{111}
)
}
が初期状態です。これに、Toffoli(CCX)の制御反転バージョンを適用します。
つまり、Ctrlビットが、両方とも$0$のときに、標的ビットに$X(Not)$が掛かるので、
下記となります(青が制御、赤が反転した標的)
\displaylines{
\frac{1}{2\sqrt{2}}(
\ket{\color{blue}{00}\color{red}{1}}+\ket{010}+\ket{100}+\ket{110}
-
\ket{\color{blue}{00}\color{red}{0}}-\ket{011}-\ket{101}-\ket{111}
)
\\
=
\frac{1}{2}
\left(
\color{red}{-1}\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\otimes
\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})
\\
=
\frac{1}{2}
\left(
\color{red}{-1}\ket{00}+\ket{01}+\ket{10}+\ket{11}
\right)
\otimes
\ket{-}_{work}
}
無事、$\ket{00}$の位相を反転することができました。
Oracle work bitを使ったほうが、Oracleの指定は柔軟ですが、$CtrlZ$で反転できる対象の場合は、$CtrlZ$を使うほうが回路がシンプルな気がします。
まとめ
Oracleを$CtrlZ$でなく、Oracle work bitを利用し実装しました。
- work bitを$(\ket{0}\color{red}{-1}\ket{1})/\sqrt{2}$で準備し、この$\color{red}{-1}$をうまく使う
- $CCX$ゲートで、探索対象の量子状態の相対位相をうまく反転させる。
といった、処理の流れでした。
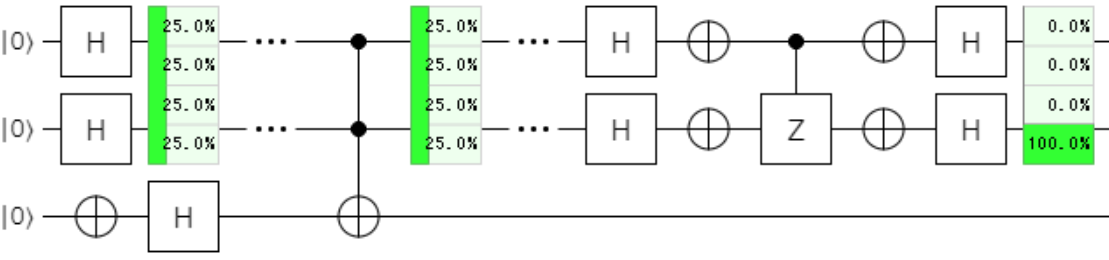
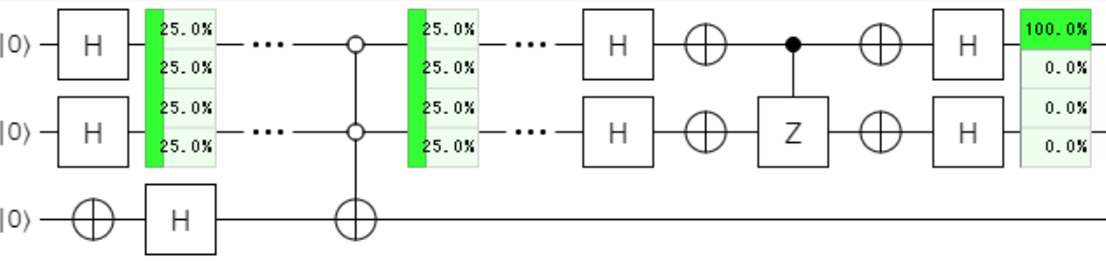
全パターンの指定を下記に示し、まとめとさせていただきたいと思います。
関連記事