はじめに
複数の選択肢の中から、所望の状態を見つけ出すGroverのアルゴリズム。
下記では、簡単のために2-bitのGrover Searchをあつかってきましたが、
最後に、3-bitバージョンもやってみたいと思います。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
$$
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \ #3 & #4 \end{bmatrix}}
$$
2bit Groverの構成部品
2bit Grover Search@Quirkは下記のような回路で構成でき、
構成部品としては、
| Oracle | IAM(Inversion About Mean) |
|---|---|
 |
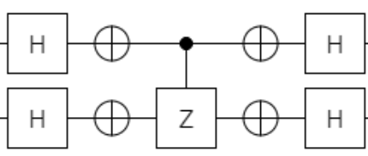 |
でした、では3bitのときは、どう構成すれば良いでしょうか?
Oracle
要領は2ビットのときと同様です。探索対象の相対位相をマイナスにマーキングすればよいので、
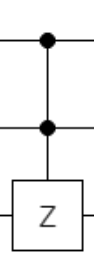
$\ket{111}$が探索対象であれば、下記の様に指定します。
IAM(Inversion About Mean)
こちらも、2bitの時は、
IAM_{2bit} = H^{\otimes{2}}(2\ket{00}\bra{00}-I)H^{\otimes{2}}
で、回路としては下記でした。
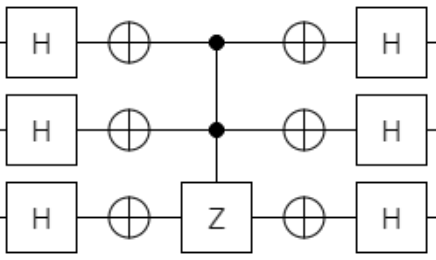
3bitになると同様の要領で、
IAM_{3bit} = H^{\otimes{3}}(2\ket{000}\bra{000}-I)H^{\otimes{3}}
となります。
動かしてみる
Grover Operatorを1回適用
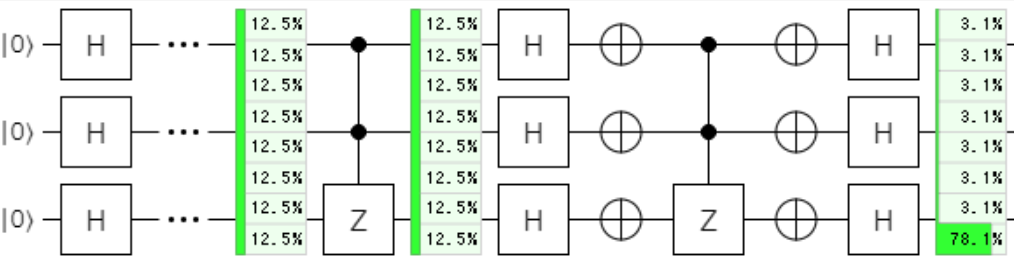
上記で構成した、Grover Operatorを1回適用してみます。
上記ですと、探索の対象である、$\ket{111}$が測定により観測できる確率は、78%です。
ちょっと、物足りないです。
そうです。Grover Operatorの適用回数はデータ数によって変わるので、Operatorの適用回数が足りていません。
なので、足しましょう。
Grover Operatorを2回適用
Grover Operatorを2回適用してみます。
これで、探索の対象である、$\ket{111}$が測定により観測できる確率は、94.5%です。
無事に所望の結果が得られそうです。
で、実を言うと、3回適用する(適用回数過多)だと所望の状態は観測できないのです。
詳細は、下記参照頂きたいですがいい塩梅が重要とおぼえておいていただければ幸いです。
まとめ
補足記事として、3-bitのときのGrover Searchを確認しておきました。
これ以上はビット数が増えても同一のやり方を繰返すだけです。
若干、冗長な感じになりましたが、どなたかのお役に立てばと。
何かありましたら、コメント。よろしければLTGMいただけると嬉しいです。
関連記事