こんにちは、VASILYバックエンドエンジニアの塩崎です。
最近ニューラルネットワークが流行っており、毎日のようにニューラルネットワークを活用した技術のニュースを目にします。
アメリカの調査機関であるGartnerが今年に発表した資料によると、「期待のピーク期」にあるそうですね。
Top Trends in the Gartner Hype Cycle for Emerging Technologies, 2017
VASILYでもファッション分野におけるユーザー課題を解決するために、データサイエンティストが様々な試みを行っています。
それらについては、以下のTECH BLOG記事に成果が書かれているので、興味のある方は是非お読みください。
VAEとGANを活用したファッションアイテム検索システム
ディープラーニングによるファッションアイテム検出と検索
さて、この記事ではそのような課題解決的な側面から離れ、アナログコンピューターでニューラルネットワークを実装するということを試みてみます。
動機
現在あるニューラルネットワークの実装はどれもデジタルコンピューターの上で動くソフトウェアとして実装されています。
これらのコンピューターの内部構造は電子回路的に見た場合にはノイマン型アーキテクチャやそれの延長線上にあるものです。
ニューラルネットワークが表現しているニューロン間のつながりという構造は、ハードウェア的には消失しています。
そのため、これらの構造をハードウェア的な結線情報という直接的な表現として持つコンピューターを作ってみました。
また、それをデジタルでやっても面白くなさそうだったので、アナログでやってみました。
アナログコンピューターとは
デジタルコンピューター
アナログコンピューターの話に入る前に、その対比としてデジタルコンピューターの話をします。
みなさんがこの記事を読むために使用しているコンピューターや、身の回りにあるほぼすべてのコンピューターはデジタルコンピューターです。
デジタルコンピューターではある時点で1本の線で表現できる情報は0か1だけ(bit)です。
当然、これだけですと表現能力に乏しすぎますので、複数のbitを利用して情報を伝達します。
情報を0か1の集まりに変換することを符号化といいます。
整数の符号化には非負整数では2進数をそのまま用い、負数では2の補数を用いることが一般的です。
また、浮動小数点数の符号化にはIEEE754が用いられることが一般的です。
例えば、123という整数を32bitで表現すると、00000000000000000000000001111011 になります。
[123].pack('N').unpack('B*').first
# => 00000000000000000000000001111011
また、1.23という浮動小数点数をIEEE754形式の倍精度浮動小数点数で表すと、 0011111111110011101011100001010001111010111000010100011110101110になります。
[1.23].pack('G').unpack('B*').first
# => 0011111111110011101011100001010001111010111000010100011110101110
そして、これらの符号化された情報に対して、加減算などの演算を行う回路(CPU)や記録を行う回路(レジスタ、RAM、ROM)などを組み合わせることで構築された計算機がデジタルコンピューターです。
アナログコンピューター
一方でアナログコンピューターは1本の線を0か1かにしか使わないなんてケチくさいことはせずに、1本の線で任意の値を表現します。
例えば、1.23という数を表現するために、その線の電圧を1.23Vにします。
デジタル式では64本もの線を使って1.23という数を表現していたことを考えると、必要な線の本数はわずか1/64で済みます。
これだけですと、アナログコンピューターの方が集積度を上げられてすごいような気がしますが、実際はそうではありません。
アナログコンピューターはデジタル式と比べてノイズに弱いという致命的な欠点があります。
例えば、デジタルコンピューターで情報電圧を行うための一規格である3.3V LVCMOSでは、電圧で情報伝達を行います。
受信側の受信した電圧が1.65V以上か以下かで情報が1か0かを決めます。
そのため、情報の送信側が3.3Vで情報を送信した場合、1.65Vよりも小さいノイズであれば、受信側は正常に受け取ることができます。
許容されるノイズ量の最大値をノイズマージンと呼び、3.3V LVCMOSであればノイズマージンは1.65Vです。
一方のアナログ式では1.23Vという電圧値そのものが意味を持っているので、ノイズマージンはゼロです。
わずかでもノイズが乗ってしまった場合は正しく情報を伝えることができなくなります。
そのため、数十年前にアナログコンピューターはデジタルコンピューターに駆逐されました。
今回は趣味での実装なので、耐ノイズ性についてはあまり考えずに進めてみましょうw
ニューラルネットワークの材料
まず、今回のアナログコンピューターでのニューラルネットワーク製作では、ネットワークのパラメーターの学習についてはデジタルコンピューターで行うこととします。
そのため、何かしらの学習済みのモデルを順伝搬させることだけについて考えます。
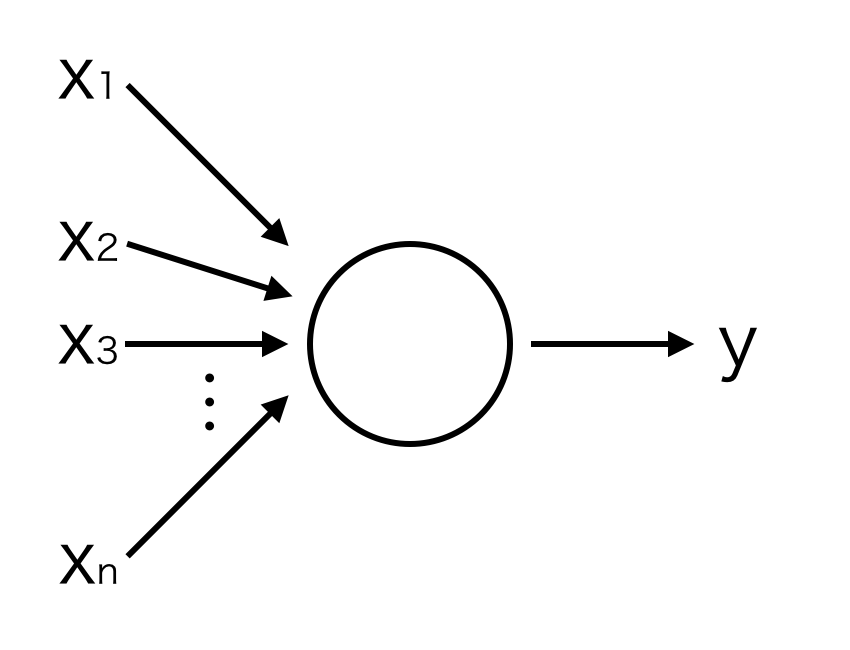
ニューラルネットワークの構成要素であるニューロンは、以下のように多数の入力を受けて1つの出力を行います。
入力と出力の関係は以下の式で与えられます。
ここで、wは重みと呼ばれるニューロン毎に設定されるパラメーターで、各入力値をどの程度出力に反映させるのかを決めます。
また、fは活性化関数と呼ばれる非線形関数です。
活性化関数には、シグモイド関数やReLUなどが使用されることが多いようです。
y = f \left( \sum_{i=1}^n w_i x_i \right)
このニューロンを多数組み合わせたものをニューラルネットワークと呼びます。
ニューロンをアナログコンピューターで実装することができれば、それの集合体であるニューラルネットワークもアナログコンピューターで実装できたことになります。
そのために、重み付き加減算回路と理想ダイオード回路を使用します。
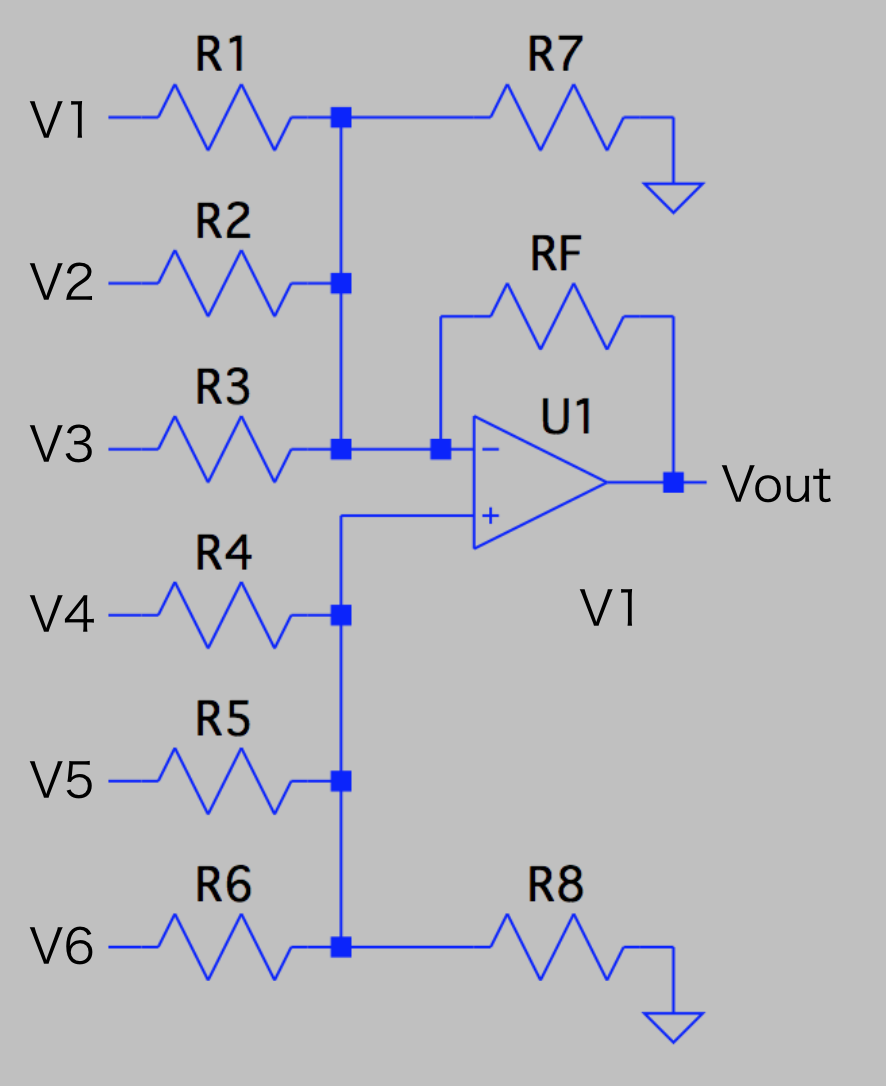
重み付き加減算回路
まずは重み付き加減算回路を紹介します。
この回路はR7とR8の抵抗値を適切に設定することによって、以下のような出力電圧Voutを出力します。
V_{out} = - \left( \frac{R_f}{R_1} V_1 + \frac{R_f}{R_2} V_2 + \frac{R_f}{R_2} V_3 \right) + \left( \frac{R_f}{R_4} V_4 + \frac{R_f}{R_5} V_5 + \frac{R_f}{R_6} V_6 \right)
これは、ニューロンの動作を表す式中の以下の部分に相当します。
\sum_{i=1}^n w_i x_i
この回路に使用されている三角形の中に+と-が書かれた電子部品はオペアンプと呼ばれる回路素子です。
オペアンプは非反転入力端子(+マークが描かれた端子)と反転入力端子(-マークが描かれた端子)の間の電圧差を増幅して出力端子(右側の端子)に出力します。
増幅率は理想的には無限大です。
そのままの状態で使うと、増幅率が高すぎて使うものにならないため、帰還抵抗Rfを通して出力の一部を入力側に返すことで増幅率を調節します。
このような使い方を負帰還をかけて使うといいます。
負帰還がかかることによって、オペアンプは非反転入力端子と反転入力端子の間の電圧差をゼロにするように働きます。
この働きを仮想短絡と呼びます。
本当はつながっていないのに(仮想)、電圧が等しくなる(短絡)という意味です。
さて、ここまでくれば、この回路の動作を説明できます。
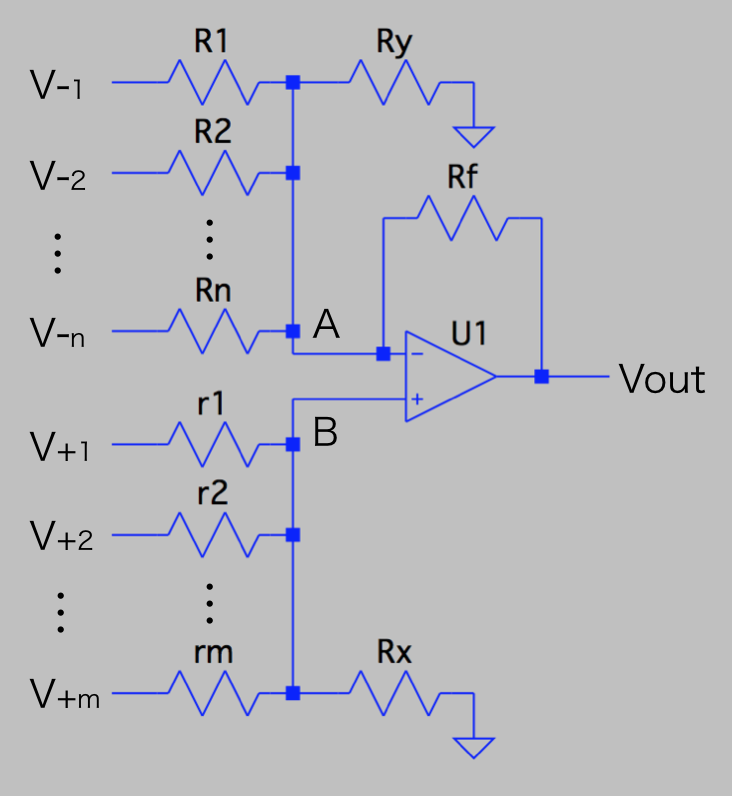
入力の個数を一般化した、以下の回路で考えることにします。
抵抗の個数はn+m+3個なのに対して、制約条件である重みはn+m個しかありません。
そのため、任意の制約条件を最大で3個追加することができます。
まず、A点に対してキルヒホッフの第一法則を使うと、以下の式が成立します。
V_{-} = (R_1 // R_2 // \cdots // R_n // R_y // R_f) \left\{ \sum_{i=1}^n \frac{V_{-i}}{R_i} + \frac{V_{out}}{R_f} \right\}
ただし、R1 // R2 // ... // RnはR1〜Rnを並列接続した時の合成抵抗値で、以下の式で定義されます。
R_1 // R_2 // \cdots // R_n = \left( \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n} \right)^{-1}
また、B点に対してキルヒホッフの第一法則を使うと、以下の式が成立します。
V_{+} = (r_1 // r_2 // \cdots // r_m // R_x) \left\{ \sum_{j=1}^m \frac{V_{+j}}{r_j} \right\}
仮想短絡により、V- = V+ なので、Voutについて式を解くと、
V_{out} = - \sum_{i=1}^{n} \frac{R_f}{R_i} V_{-i} + \frac{r_1 // r_2 // \cdots // r_m // R_x}{R_1 // R_2 // \cdots // R_n // R_y // R_f} \sum_{j=1}^{m} \frac{R_f}{r_j} V_{+j}
を得ます。
ここで、以下の式が成り立てば、重みはシンプルな抵抗値の比になります。
そのため、これを新たな制約条件に加えます。
\frac{r_1 // r_2 // \cdots // r_m // R_x}{R_1 // R_2 // \cdots // R_n // R_y // R_f} = 1
とはいえ、このままではこの制約条件は扱いづらいので、式変形をしてこの条件を十分に満たす綺麗な条件を見つけることにします。
以下のように、Xi、Yj、X、Yを定義します。
Y_i = \frac{R_f}{R_i}, X_j = \frac{R_f}{r_j}, Y = \sum_{i=1}^n Y_i, X = \sum_{j=1}^n X_j
すると、制約条件の式はシンプルな形になります。
X - Y - 1 = R_f \left( \frac{1}{R_y} - \frac{1}{R_x} \right)
抵抗値が正の値しか取れないことを考えると、X - Y - 1の正負によって、適切にRy、Rxを設定するための条件が変わります。
X - Y - 1 > 0の場合は、以下の条件を満たせば、制約条件を十分に満たします。
\begin{cases}
R_x = \infty \\
R_y = \frac{R_f}{X - Y - 1}
\end{cases}
X - Y - 1 < 0の場合は、以下の条件を満たせば、制約条件を十分に満たします。
\begin{cases}
R_x = - \frac{R_f}{X - Y - 1} \\
R_y = \infty
\end{cases}
そして、X - Y - 1 = 0の場合は、以下の条件を満たせば、制約条件を十分に満たします。
\begin{cases}
R_x = \infty \\
R_y = \infty
\end{cases}
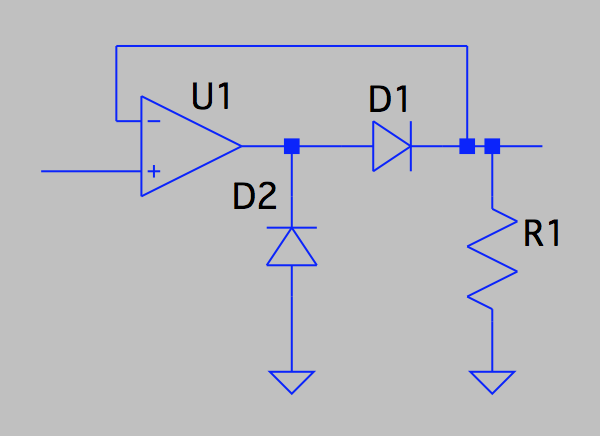
理想ダイオード回路
次に理想ダイオード回路を紹介します。
この回路は入力電圧が正の時には入力電圧と同じ電圧を出力し、負の時には0Vを出力します。
V_{out} = \begin{cases}
V_{in} & (V_{in} > 0) \\
0 & (otherwise)
\end{cases}
これは、ニューロンの動作を表す式中の活性化関数fに相当します。
ニューラルネットワーク界隈でReLUと呼ばれている活性化関数と同等の働きをします。
入力電圧の正負によって、負帰還がかかるかどうかが変化するために、このような動作をします。
試しに設計してみる
それでは、試しに何かしらのニューラルネットワークを実装してみることにしましょう。
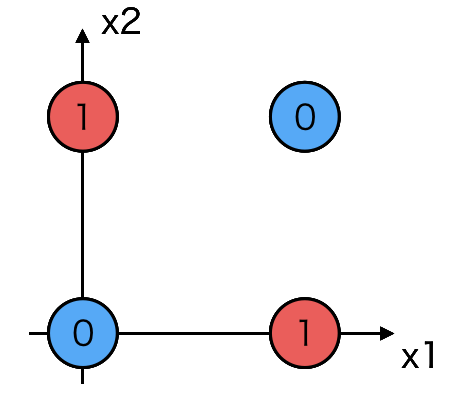
ここでは、XORの機能を持つニューラルネットワークを実装してみます。
XORは0 or 1の値をとる2つの入力値(x1, x2)と、1つの出力値(y)を持ちます。
x1とx2が一致するときには、yは0になり、不一致するときにはyは1になります。
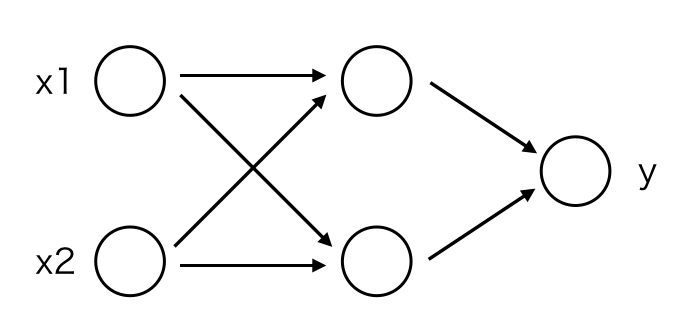
線形分離不可能なので、隠れ層を持つ3層ニューラルネットワークでXORを表現することにします。
重みの決定
ニューラルネットワークの重みの学習についてはデジタルコンピューターで行います。
Chainerを使って学習を行います。
import numpy as np
train = [
(np.array([0, 0], dtype=np.float32), np.array([0], dtype=np.float32)),
(np.array([0, 1], dtype=np.float32), np.array([1], dtype=np.float32)),
(np.array([1, 0], dtype=np.float32), np.array([1], dtype=np.float32)),
(np.array([1, 1], dtype=np.float32), np.array([0], dtype=np.float32))
]
test = [
(np.array([0, 0], dtype=np.float32), np.array([0], dtype=np.float32)),
(np.array([0, 1], dtype=np.float32), np.array([1], dtype=np.float32)),
(np.array([1, 0], dtype=np.float32), np.array([1], dtype=np.float32)),
(np.array([1, 1], dtype=np.float32), np.array([0], dtype=np.float32))
]
from chainer import iterators
batchsize = 4
train_iter = iterators.SerialIterator(train, batchsize)
test_iter = iterators.SerialIterator(test, batchsize,
repeat=False, shuffle=False)
import chainer
import chainer.links as L
import chainer.functions as F
class MLP(chainer.Chain):
def __init__(self):
super(MLP, self).__init__()
with self.init_scope():
self.l1 = L.Linear(2, 2)
self.l2 = L.Linear(2, 1)
def __call__(self, x):
h1 = F.relu(self.l1(x))
return self.l2(h1)
model = MLP()
from chainer import optimizers
optimizer = optimizers.SGD(lr=0.01)
optimizer.setup(model)
from chainer.dataset import concat_examples
max_epoch = 100000
while train_iter.epoch < max_epoch:
train_batch = train_iter.next()
x, t = concat_examples(train_batch)
y = model(x)
loss = F.mean_squared_error(y, t)
model.cleargrads()
loss.backward()
optimizer.update()
抵抗値の決定
学習済みのモデルに対して、以下のようにすることで、モデルのパラメーターを表示することができます。
print(model.l1.W)
print(model.l2.W)
print(model.l1.b)
print(model.l2.b)
そして、それらの結果を重み付き加減算回路の式に当てはめることによって、抵抗値が決まります。
抵抗値の決定はただ公式に当てはめるだけなので、ここでは省略します。
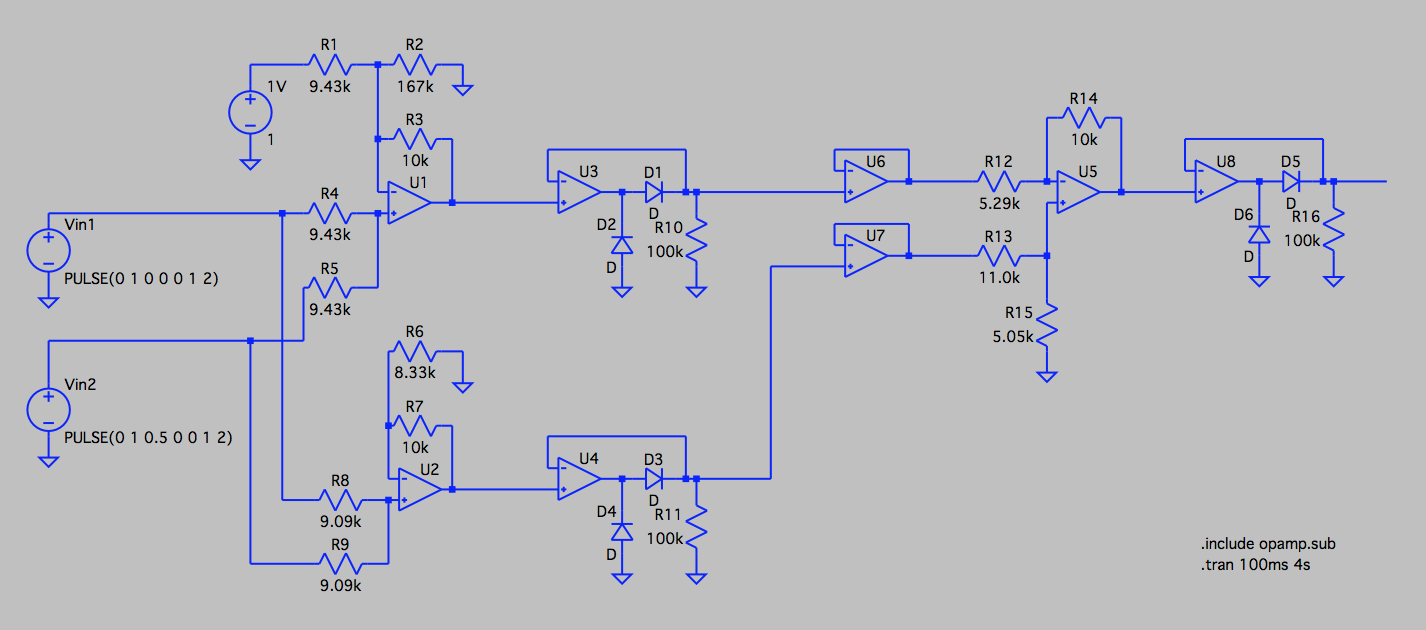
そして、完成したニューラルケットワークが以下のようなものです。
理想ダイオード回路の出力インピーダンスがゼロではないので、出力インピーダンスをゼロにするために、後段にボルテージフォロア回路をつけました。
動作確認を行ってみる
ニューラルネットワークを実装できたので、次にこのネットワークの動作確認を行ってみます。
動作確認には回路シミュレータであるLTSpiceを使用します。
この回路シミュレータはLinearTechnology社が無料で公開しているもので、アナログ回路のシミュレーションを行うことができます。
LTSpiceはDC解析やAC解析などの様々なSPICEコマンドを受け付けることができます。
今回は入力電圧を時間的に変化させた時の出力電圧の時間的な変化を観察するために、トランジット解析を行います。
電圧源
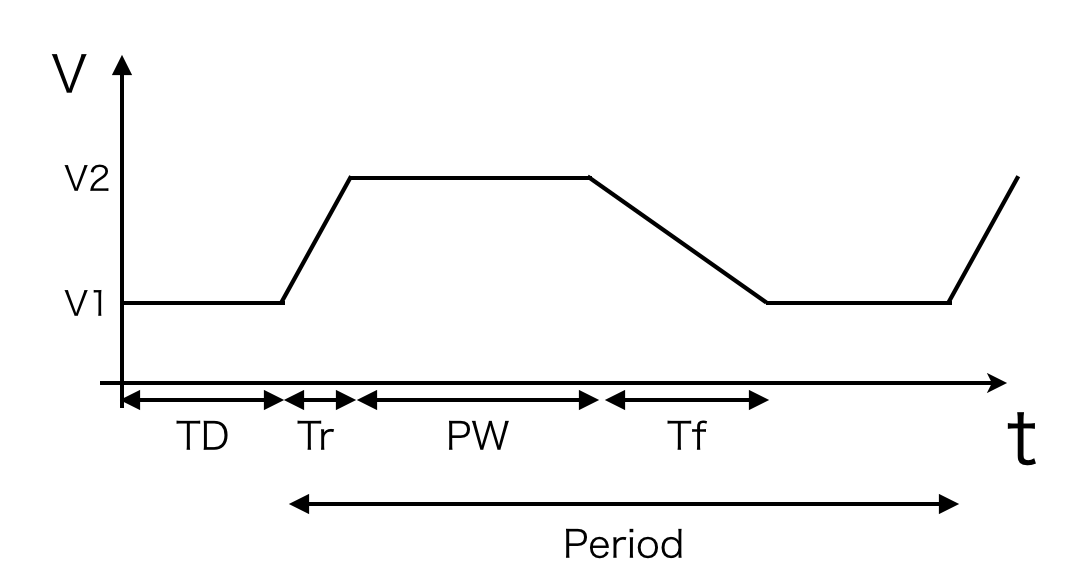
まずは、入力電圧を時間的に変化させるためにPLUSE文を使用します。
PULSE文はパルス波を出力するための文で、PULSE(V1 V2 TD Tr Tf PW Period) のように使用します。
それぞれの引数は下の図に表すような意味を持ちます。
今回は、2つのパルス電圧源にそれぞれ以下のようなPULSE文を設定することで、半周期ずれたパルスを入力することにします。
Vin1 PULSE(0 1 0 0 0 1 2)
Vin2 PULSE(0 1 0.5 0 0 1 2)
トランジット解析
トランジット解析のためには、.TRAN文を使用します。
.TRAN文は.TRAN TSTEP TSTOPのように使用します。
0〜TSTOPまでの期間をTSTEP刻みで解析を行うという意味です。
今回は、.TRAN 100ms 4s という.TRAN文を設定します。
結果
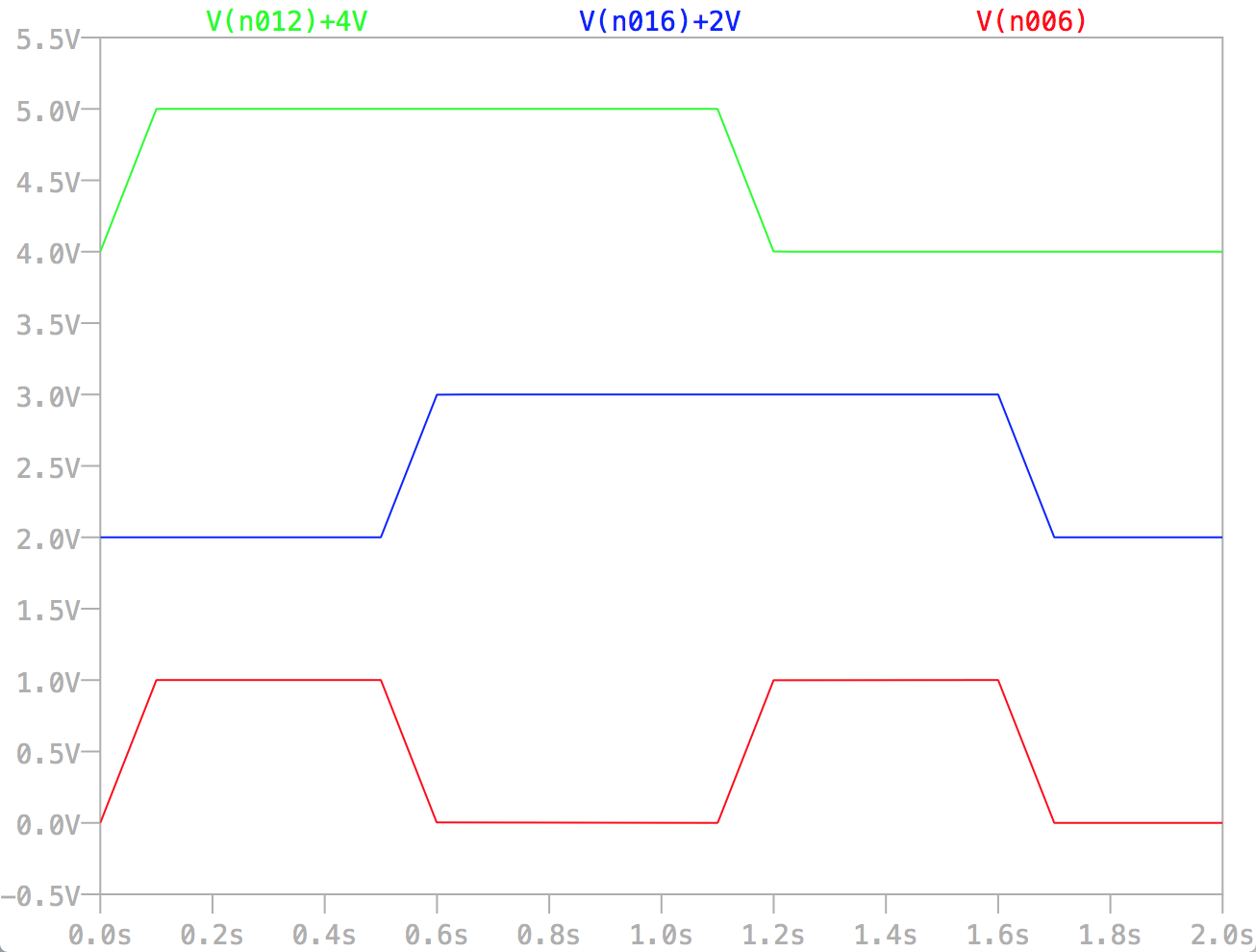
入出力の時間変化を以下のグラフに示します。
緑の線がVin1、青の線がVin2、赤の線がVoutです。
すべての線のベースラインを揃えると、線が重なってしまい見づらいです。
そのために、緑と青の線にはそれぞれ、+4Vと+2Vのオフセットをあたえてあります。
このグラフから、(Vin1, Vin2)が(0, 0), (0, 1), (1, 0), (1, 1)のすべての場合で、Vout = Vin1 XOR Vin2 を満たしていることが確認できます。
ただXORの機能を使うだけであれば、74HC86などのロジックICとなんら変わりませんが、すべての演算をアナログで行っているところがこの回路の特徴です。
まとめ
非常にシンプルなニューラルネットワークをアナログコンピューターの方法で実装し、回路シミュレーターで動作確認することに成功しました。
今回実装したニューラルネットワークは階層型なのでとても簡単に実装することができました。
今度はホップフィールド型などのニューラルネットワークの実装にも挑戦してみたいです。