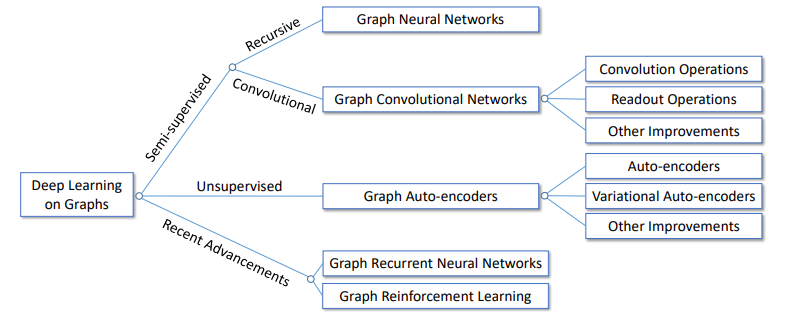
はじめに
本記事は3部作の最終回です. 記号の定義などは第1回の記事をご参照ください.
GNNまとめ(1): GCNの導入 - Qiita
種々のGCNを紹介した第2回の記事はこちら.
GNNまとめ(2): 様々なSpatial GCN - Qiita
今回はautoencodersによるグラフ埋め込みの獲得やGAN, 時間発展のあるグラフなど発展的な事項を扱います.
[1]より引用.
その他
第1部, 第2部の小見出しを受けて「その他」という名目でまとめます.
AE/VAE
前回までグラフの埋め込みを得るための畳込みについて考えてきましたが, 画像において行われているように, autoencoderやVAEを用いて教師なしの表現学習をしたいと思うのは自然な流れです. しかし, 畳込みの逆演算としてのdecodeの方法は自明ではありません.
本記事では, ニューラルネットを使わずにdecodeする方法と, 全結合のニューラルネットでdecodeする方法の2通りを紹介します.
GAE/VGAE
グラフ界の重鎮であるKipfとWellingが提案した, グラフを扱うAutoencoderとVAEの元祖です. 元祖なので詳しく説明します.
隣接行列を入出力とし, encoderをGCN (Kipf+)で, decoderを内積とシグモイド関数のみで構成します.
入力にノード特徴を含めることもできます.
GAE (graph autoencoder) の式はこのようになります.
\boldsymbol{H} = GCN(\boldsymbol{F}^V,\boldsymbol{A})\\
\hat{\boldsymbol{A}} = sigmoid(\boldsymbol{HH}^{\mathrm{T}})
VGAE (variational graph autoencoder) の場合はreparametrization trickの平均と標準偏差をそれぞれ$\boldsymbol{\mu}, \boldsymbol{\sigma}$として, それぞれを2層のGCNで求めます. これがencoderに当たります.
\boldsymbol{\mu} = GCN_{\boldsymbol{\mu}}(\boldsymbol{F}^V,\boldsymbol{A})\\
\log\boldsymbol{\sigma} = GCN_{\boldsymbol{\sigma}}(\boldsymbol{F}^V,\boldsymbol{A})
ノード$i$の潜在ベクトル$\boldsymbol{h}_i$は$\boldsymbol{\mu}, \boldsymbol{\sigma}$でパラメトライズされた正規分布に従うとして,
q(\boldsymbol{h}_i|\boldsymbol{F}^V,\boldsymbol{A})
= \mathcal{Norm}(\boldsymbol{h}_i|\boldsymbol{\mu}_i, \boldsymbol{\sigma_i})
からサンプリングされます. decoderは次のように確率分布の形で書けます.
p(A_{i,j}=1|\boldsymbol{h}_i, \boldsymbol{h}_j) = sigmoid(\boldsymbol{h}_i^{\mathrm{T}}\boldsymbol{h}_j)
全ノードについてまとめた分布は単純な積で表せます.
q(\boldsymbol{H}|\boldsymbol{F}^V,\boldsymbol{A}) = \prod_{i=1}^N q(\boldsymbol{h}_i|\boldsymbol{F}^V,\boldsymbol{A})\\
p(\boldsymbol{A}|\boldsymbol{H}) = \prod_{i=1}^N \prod_{j=1}^N p(A_{ij}=1|\boldsymbol{h}_i, \boldsymbol{h}_j)
それから, 変分下限を次のように定めて最大化することでモデルを学習させます.
ELBO = \mathbb{E}_{q(\boldsymbol{H}|\boldsymbol{F}^V,\boldsymbol{A})}[\log p(\boldsymbol{A}|\boldsymbol{H}) ] - D_{KL}[q(\boldsymbol{H}|\boldsymbol{F}^V,\boldsymbol{A})||p(\boldsymbol{H})]
*VGAEを取り上げている[1]と[3]では両方とも「変分下限を最小化」と書いてありましたが, おそらく間違っているので「最大化」と直してあります. 原著論文でも"optimize"としか書いていなかったので紛らわしいですね. [1]は特に, 転置するベクトルを取り違えていたりもしていて, ここに限らず間違いが散見されます.
[Variational Graph Auto-Encoders](https://arxiv.org/abs/1611.07308)
SDNE
SDNE (structural deep network embedding) は次のように損失関数の改良を提案したものです.
Loss = \sum_{i=1}^N||(\hat{\boldsymbol{A}}_i-\boldsymbol{A}_i)\odot\boldsymbol{b}_i||_2^2
+ \alpha\sum_{i=1}^N\sum_{j=1}^N A_{i,j}||\boldsymbol{h}_i-\boldsymbol{h}_j||_2^2
第1項は通常の再構成誤差に$\boldsymbol{b}_i$というハイパーパラメータを加えたものです.
b_{i,j} = \begin{cases}
1 &A_{i,j}=0\\
\beta (>1) &\text{otherwise}\\
\end{cases}
非ゼロ成分のときに誤差を大きくすることで疎な隣接行列をうまく扱えるそうです.
第2項はLaplacian Eigenmapsにと対応する項と書かれていますが, 私には難しくてよくわかりません.
[Structural Deep Network Embedding](https://dl.acm.org/citation.cfm?id=2939753)
DNGR
DNGR (deep neural networks for graph representations) は隣接行列や遷移行列ではなくPPMI(positive pointwise mutual information)行列を再構成するアプローチです. これによって, グラフ上をランダムウォークしたときに各ノードを訪れる確率が特徴として取り込まれます.
[Deep Neural Networks for Learning Graph Representations](https://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/view/12423)
DRNE
DRNE (deep recursive network embedding) はノードの潜在ベクトルを再構成するという特殊なautoencoderです(原著ではautoencoderとは呼ばれていません).
具体的には, 参照ノードの潜在ベクトルを隣接ノードの集約によって再構成するというアプローチです. 集約関数にはLSTMが用いられます.
次の損失関数の最小化でLSTMを学習させます.
Loss = \sum_{i=1}^N ||\boldsymbol{h}_i-\mathrm{LSTM}(\{ \boldsymbol{h}_j|j \in \mathcal{N(i)} \})||_2^2
[Deep Recursive Network Embedding with Regular Equivalence](https://dl.acm.org/citation.cfm?doid=3219819.3220068)
ARGA/ARVGA
adversarial trainingを利用したAE/VAEもあります.
ARGA (adversarially regularized graph autoencoder) とARVGA (adversarially regularized variational graph autoencoder) は, 隣接行列$\boldsymbol{A}$とノード特徴$\boldsymbol{F}^V$を潜在ベクトルの系列$\boldsymbol{H}$にencodeし, $\boldsymbol{H}$から$\hat{\boldsymbol{A}}$をdecodeするという枠組みはGAE/VGAEと同じですが, $\boldsymbol{H}$に関して真贋判定を行う識別器を用意しているところが特徴です. 識別器を潜在ベクトルに対して作用させるのは画像のGANでも見たことがありません.
識別器は, $\boldsymbol{H}$が事前分布(一様分布や正規分布)からサンプルされたもの(real)かグラフをGCNでencodeして得られたもの(fake)かを判定します.
これによりadversarial lossが計算され, recontruction lossと合わせた損失関数を最小化することで, $\boldsymbol{H}$は事前分布に近くかつグラフの特徴を保存した表現になります.
GAE, VGAEに対応するものがそれぞれARGA, ARVGAです.
[Learning Graph Embedding with Adversarial Training Methods](https://arxiv.org/abs/1901.01250)
GraphVAE
GraphVAE は, これまでに紹介したVAEとは異なり, 全結合のネットワークで$\boldsymbol{h}$から隣接行列$\hat{\boldsymbol{A}}$, エッジ特徴のテンソル$\hat{\boldsymbol{F}^E}$, ノード特徴$\hat{\boldsymbol{F}^V}$を再構成します.
グラフには最大のノード数$k$を設定します. また, エッジのクラス数を$C_E$, ノードのクラス数を$C_V$とします.
再構成する$\hat{\boldsymbol{A}} \in \mathbb{R}^{k \times k}, \hat{\boldsymbol{F}^E} \in \mathbb{R}^{k \times k \times C_E}, \hat{\boldsymbol{F}^V} \in \mathbb{R}^{k \times C_V}$はそれぞれ, エッジの確率分布, エッジのクラスに関する確率分布, ノードのクラスに関する確率分布を想定しています. 存在しないノードについてはゼロ埋めで対処することで, 異なるノード数のグラフを全結合ネットワークで扱えるようになります.
再構成誤差の計算にも工夫があります. 詳細は割愛しますが, MPM(max-pooling matching; 最大値プーリングマッチング)という2つのグラフのノード同士を対応付けるアルゴリズムを使って損失を定義します. しかし, ここの計算量が$O(N^4)$なので, 小さいグラフ(論文では$k=38$)にしか適用できない点が課題です.
[GraphVAE: Towards Generation of Small Graphs Using Variational Autoencoders](https://arxiv.org/abs/1802.03480)
JT-VAE
サーベイ論文には載っていませんでしたが, グラフを木に簡約化してGRUなどでencode/decodeするJT-VAE (junction tree VAE) というアプローチもあります.
GCNから話が逸れてしまうので詳しくは論文を参照していただきたいと思いますが, 図のように, 分子グラフを環構造をまとめて1つのノードに置き換えることで閉路のない木に変換することができます(木分解).
[Junction Tree Variational Autoencoder for Molecular Graph Generation](https://arxiv.org/abs/1802.04364)
GAN+強化学習
VAEがあるならGANもあります. グラフ一般ではなく, 小分子のグラフを生成する研究がほとんどのようです.
また, 分子の特性の最適化のために強化学習の枠組みを取り入れているものが多いです.
MolGAN
MolGAN (molecular GAN) は, 生成器を多層パーセプトロン, 識別器をR-GCNとGGS-NNで構成したWasserstein GANです. 隣接行列$\hat{\boldsymbol{A}}$とノード特徴$\hat{\boldsymbol{F}^V}$を生成・識別します.
この論文は所望の特性を持つ分子の生成を目的としているので, ただの分子を生成するのでは意味がありません.
そこで, 強化学習の報酬の考え方を取り入れて, 生成された分子の「実用の観点から見た」評価を行います. 識別器と同じ構造を持つ報酬ネットワークを用意し, DDPGで分子の特性を学習させます.
生成器の損失関数はWGANの損失と報酬ネットワークから得られるスコアの損失の線形和で定義します.
[MolGAN: An implicit generative model for small molecular graphs](https://arxiv.org/abs/1805.11973)
GCPN
GCPN (graph convolutional policy network) は強化学習をもっと活用したアルゴリズムで, 分子グラフの生成過程をマルコフ決定過程として捉えます.
状態は生成途中の分子グラフ, 行動は次に繋ぐ原子と結合次数の選択です. 報酬は, 原子価ルールを守れているかのスコア(step reward), 分子の特性(LogPやQED)に関するスコア(final reward), 教師データの分布に近づけるためのadversarial rewardの合計で与えます.
強化学習のアルゴリズムはPPOを使います.
方策関数と識別器はGCN(Kipf+)をベースに設計します. エッジのクラス数を$C_E$として, クラスごとに畳み込んでから集約します.
\boldsymbol{H}^{l+1} = \mathrm{AGGREGATE}(
\mathrm{ReLU} (\{\boldsymbol{\tilde{D}}_i^{- \frac{1}{2}}\boldsymbol{\tilde{A}}_i\boldsymbol{\tilde{D}}_i^{- \frac{1}{2}}\boldsymbol{H}^l\boldsymbol{\Theta}_i^l, ~\forall i\in(1,...,C_E)\} )
)
集約関数の候補には平均, 最大値, 和, 結合がありますが, 和の場合が最もよく機能するそうです. 集約関数の話は[5]が詳しいです.
[Graph Convolutional Policy Network for Goal-Directed Molecular Graph Generation](https://arxiv.org/abs/1806.02473)
RNN
グラフの時間発展を扱うために, RNNを組み込んだGNNもあります. まだ勉強中なので, 簡単な紹介に留めさせてください.
DGNN
DGNN (dynamic GNN) は, 新たなノードやエッジの出現に対応して各ノードやグラフの潜在ベクトルを更新するためにLSTMを利用しています.
[Streaming Graph Neural Networks](https://arxiv.org/abs/1810.10627)
DGCN
DGCN (dynamic GCN) はGCNとLSTMを組み合わせたものです.
[Dynamic Graph Convolutional Networks](https://arxiv.org/abs/1704.06199)
今後の課題
今後の研究の方向性として, 以下のような視点が挙げられています.
- 多様なグラフ
無向/有向, 重み付き/なし, ラベル付き/なし, 大規模/小規模…といった様々なグラフに対して汎用に使えるアルゴリズムがあると便利ですよね. - 動的グラフ
参考文献でも本記事でもあまり大きく扱われませんでしたが, 動的グラフは今でもうまく扱えていないようです. 一方で, 交通網やwebやSNSなどグラフが時間的に変化する実例はとても多いので, 今後のGNNについて最も期待されている部分だと思います. - 多層化
GNNは2, 3層程度のものが多く, 152層のResNetのように深いネットワークでの学習はまだ成功していません. ただし, 理論的には畳込みを繰り返すとすべてのノードの潜在ベクトルが1点に収束するらしく, そもそも深いネットワークでの学習が有効なのかもわかっていません. - スケーラビリティ
第1部の冒頭でも同じことを書いています. これまでいろいろなモデルを見てきましたが, 特にGANはスケーラビリティが大きな課題となっていますね.
おわりに
深層学習のグラフへの適用は比較的新しい分野で教科書などもないので, なかなか手を出しづらいという方が(私も含め)多かったのではないでしょうか. この記事を書いてとても勉強になりました.
最近Twitterでグラフの話題を見かけることが多く, 流行の兆しを感じているので, これを機にこの分野がもっと盛り上がっていったらおもしろいなと思っています.
偉そうにいろいろと書いてしまいましたが, 私もよくわかっていないことが多いです. まだ手を動かせていないので, そろそろ実際にコードを書いたりして理解をより深めていきたいと思います.
最後までお読みいただきありがとうございました！
参考文献
[1] Z. Zhang et al., Deep Learning on Graphs: A Survey, arXiv, 2018.
本記事は主にこちらの論文をベースにしています. 3本の中で一番わかりやすく感じました.
[2] J. Zhou et al., Graph Neural Networks: A Review of Methods and Applications, arXiv, 2018.
[3] Z. Wu et al., A Comprehensive Survey on Graph Neural Networks, arXiv, 2019.
[4] 論文紹介: "MolGAN: An implicit generative model for small molecular graphs"
創薬の背景についても紹介されていておもしろいです.
[5] K. Xu et al., How Powerful are Graph Neural Networks?, ICLR, 2019.