はじめに
2018年はグラフを扱う深層学習(GNN; graph neural network)が大きく発展した1年でした.
その一方で, 提案される手法が多くなるに連れて, それぞれの関係性や全体像が見えづらくなっている印象があります.
その問題を受けてか, 年末頃からこのような図を含むサーベイ論文[1-3]がarXivに立て続けに登場していたので, その内容をまとめてみました. 長いので3部作に分けようと思います.
ちなみに, 本記事に限らず, GNNという言葉は2通りの意味で用いられているので注意してください.
本記事のタイトルのようにGNNがグラフを扱う深層学習全般を指すこともあれば, 図にあるように. 畳込みを利用しないアルゴリズムを指すこともあります.
毎度のお断りですが, 以下の5点はあらかじめご了承ください.
- コードは書いていません. 概念のみの説明です
- 他のアルゴリズムの基礎となりうる重要な概念については詳しく書きました. その他については簡潔に書きました
- 深層学習についてはある程度理解している読者を想定しています
- 勉強しながらこの記事を書いています. 「この式がおかしい!」「このアルゴリズムも追加するべき!」などコメントがあればぜひお願いします
- たまに不自然な改行がありますが, これはQiitaのMarkdownでインラインの数式がうまく表示できなかったためです
グラフについて
データ構造としてのグラフ(「折れ線グラフ」や「棒グラフ」の「グラフ」とは違う)は様々な領域で登場します.
イメージしやすい例を挙げると, 交通網, web(リンクが有向エッジ), FacebookのようなSNS, 分子(原子がノードで結合がエッジ), 神経回路などがあります.
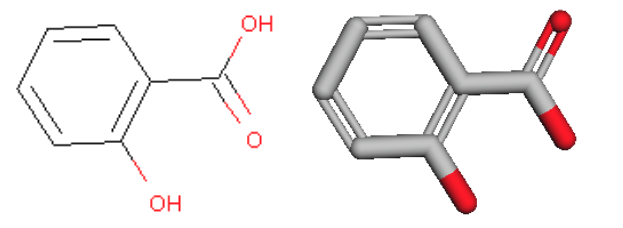
例えば分子で言うと, サリチル酸(左)はこのように表すことができます(右).
したがって, グラフの解析に機械学習が使えると様々な嬉しいことが期待できます(渋滞の予測や分子の活性予測など).
しかし, グラフは次に挙げるような難しさがあり, 画像や自然言語のようなデータに対して目覚ましい性能を見せてきた深層学習を, そのままグラフに適用することには課題がありました.
- グラフは規則的な形でない
グラフは画像のようなテンソルになっていないため, 畳込みの定義も自明ではありません. グラフ上の探索すら容易ではなく, 例えば2つのグラフが同じ形かどうかを判定する問題は多項式時間で解けるアルゴリズムが知られていません(詳しくは「グラフ同型性判定問題」で調べてみてください). - 構造やタスクの違い
ひとくちにグラフといっても, 様々な種類があります. 無向/有向, 重み付き/なし, ラベル付き/なし, 大規模/小規模などです. それぞれに対して解きたいタスクも変わってきます. 先ほどの渋滞予測の例では注目する対象がエッジの特徴の時系列的な変化ですし, 分子の活性予測ではグラフ全体に注目して何かの値を回帰することになります. そのため, タスクごとに異なるアルゴリズムを設計する必要があります. 特に, ノードとグラフのどちらに注目しているかは常に確認してください. - スケーラビリティ
webやSNSのような大規模なグラフを扱う際にはメモリと計算量がボトルネックになるため, 効率的なアルゴリズムを考案する必要があります. - ドメイン知識
先ほど「グラフは様々な領域で登場する」と書きましたが, その領域に特異な情報や制約がタスクと本質的に関わってくる場合があります. 例えば分子をグラフとして扱う場合は, 結合次数(原子価)が原子ごとに決まっており最大でもリン(P)の5程度で抑えられる, というのはアルゴリズムを考える上で重要でしょう. このような制約は積極的に活用することもできる一方で, 扱うグラフやノードの特徴を決定づけるような要素がドメインごとに異なるため, 統一的・汎用的なアルゴリズムを設計することが困難であり, 研究が分散しがちです.
これらの課題を解決しグラフで深層学習をする試みが, ここ数年で多くの研究者によってなされてきました.
本記事では, 冒頭の樹形図の中でも, 教師ありのグラフ深層学習アルゴリズムとしてグラフニューラルネットワーク(GNN; graph neural network)とグラフ畳込みネットワーク(GCN; graph convolutional network)のうちspectralなアプローチのものについて説明します.
参考文献ではSpatial GCNや生成モデル, 時系列モデルも扱われていますが, 分量の関係で次回以降の記事に譲ります.
記法と定義
以降を読み進めるにあたって必要な事柄を整理しておきます.
記法
本シリーズでは, 説明に次のような記号を用います.
細かいことですが, 変数としてのベクトルは小文字・太字・イタリック, 変数としての行列は大文字・太字・イタリックで表します(参照した論文ではなぜか立体になっていました).
| 記号 | 意味 |
|---|---|
| $V$ | ノード(node; vertex)の集合 |
| $N$ | ノードの数 |
| $E$ | エッジ(edge)の集合 |
| $M$ | エッジの数 |
| $G=(V,E)$ | グラフ(graph) |
| $\boldsymbol{F}^V, \boldsymbol{F}^E$ | ノードとエッジの特徴 |
| $\boldsymbol{A} \in \mathbb{R}^{N \times N}$ | 隣接行列(adjacency matrix) |
| $\boldsymbol{D} \in \mathbb{R}^{N \times N}$ | 次数行列(degree matrix) |
| $\boldsymbol{L} = \boldsymbol{D}-\boldsymbol{A}$ | ラプラシアン行列(Laplacian matrix) |
| $\bf{\mathcal{L}} = \boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{L}\boldsymbol{D}^{- \frac{1}{2}}$ | 正規化ラプラシアン行列 |
| $\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U}^{\rm{T}} = \boldsymbol{\mathcal{L}}$ | $\boldsymbol{\mathcal{L}}$の固有値分解 |
| $\boldsymbol{P}=\boldsymbol{D}^{-1}\boldsymbol{A}$ | 遷移行列(transition matrix) |
| $\mathcal{N}_{k}(i)$ | ノード$i$から距離$k$以内にあるノードの集合 |
| $\boldsymbol{H}^l$ | 第$l$層での潜在ベクトルを並べた行列 |
| $f_l$ | $\boldsymbol{H}^l$の次元数 |
| $\rho(\cdot)$ | 活性化関数 |
| $\odot$ | 要素積 |
| $[\cdot,\cdot]$ | 結合(concatenation) |
| $\boldsymbol{\Theta}, \boldsymbol{\theta}$ | 学習されるパラメータ(重み) |
定義
まず, 本シリーズで扱うグラフは特に記述がない限り重みなしの無向グラフとします.
このとき, グラフ$G=(V,E)$の隣接行列$\boldsymbol{A}=(a_{i,j})$は, 2つのノードが隣接しているかどうか(ノード間にエッジがあるか)を2値で表す行列であり, 次のように定義されます.
a_{i,j} = \begin{cases}
1 & ((i,j)\in E) \\
0 & (otherwise)
\end{cases}
グラフ$G$の次数行列$\boldsymbol{D}=(d_{i,j})$は, ノードが含まれるエッジの数(結合次数)を対角成分に並べた行列であり, 次のように定義されます.
d_{i,j} = \begin{cases}
\sum_{k}{a_{i,k}} & (i=j) \\
0 & (otherwise)
\end{cases}
グラフ$G$のラプラシアン行列$\boldsymbol{L}$は次のように定義されます. $\boldsymbol{A}$と$\boldsymbol{D}$は実対称行列なので, $\boldsymbol{L}$も実対称行列です.
\boldsymbol{L}=\boldsymbol{D}-\boldsymbol{A}
これをノードの次数で正規化した正規化ラプラシアン$\boldsymbol{\mathcal{L}}$もよく使われます.
\boldsymbol{\mathcal{L}} = \boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{L}\boldsymbol{D}^{- \frac{1}{2}} = \boldsymbol{I}-\boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{A}\boldsymbol{D}^{- \frac{1}{2}}
$\boldsymbol{D}^{-1}\boldsymbol{L}$や$\boldsymbol{L}\boldsymbol{D}^{-1}$は一般に非対称なので注意してください.
隣接行列, 次数行列, ラプラシアン行列, 正規化ラプラシアン行列の具体例を挙げておきます.

GNN
畳込みを使わないタイプをGNNとして最初に紹介します.
GNN
グラフを扱う深層学習の最も基本的な形です.
ノード$i$の潜在ベクトル $\boldsymbol{h}_i$ は, 次のステップで求められます.
1. 学習される関数である$\mathcal{F}(\cdot)$を用いて, 潜在ベクトル$\boldsymbol{h}_i$が収束するまで次の式を適用します. これによってノード$i$の周辺の特徴を取り込みます.
\boldsymbol{h}_i \leftarrow \sum_{j \in \mathcal{N}(i)}\mathcal{F}(\boldsymbol{h}_i, \boldsymbol{h}_j, \boldsymbol{F}^{V}_{i}, \boldsymbol{F}^{V}_{j}, \boldsymbol{F}^{E}_{i,j})
2. 学習される関数である$\mathcal{O}(\cdot)$を用いて, 出力を計算します.
\hat{y}_i = \mathcal{O}(\boldsymbol{h}_i, \boldsymbol{F}^{V}_{i})
$\mathcal{F}(\cdot)$と$\mathcal{O}(\cdot)$は通常の順伝搬型ニューラルネットでモデリングできます.
重みは, $\hat{y}_i$と教師ラベルの誤差を最小化するようにステップ1, 2と誤差逆伝搬を繰り返すことで学習されます(Almeida-Pinedaアルゴリズムと呼ばれるそうです).
なお, グラフ全体の潜在ベクトルを求めたい場合には, 全ノードと隣接しているマスターノードのようなものを仮想的に考えると, その潜在ベクトルを利用することができます.
このようにして, グラフをニューラルネットで扱う枠組みを作ることができました. この枠組みは後で紹介するGCNなどにも受け継がれています.
しかし, この方法にはいくつかの欠点があり, あまり実用的ではありません.
- $\mathcal{F}(\cdot)$が縮小写像でないとステップ1が終わらない
- ステップ1の再帰処理を繰り返すので計算量が大きい
GGS-NN
ステップ1の再帰処理をGRUで置き換えて縮小写像の制約を取り除いたものがGGS-NN(gated graph sequence nueral network) です. GGNNとも呼ばれるらしいです.
\begin{eqnarray}
\boldsymbol{m}_i &=& \sum_{j \in \mathcal{N}(i)}\theta_{e_{ij}} \boldsymbol{h}_j\\
\boldsymbol{z}_i &=& \rho(\boldsymbol{\Theta}_z[\boldsymbol{h}_i, \boldsymbol{m}_i])\\
\boldsymbol{r}_i &=& \rho(\boldsymbol{\Theta}_r[\boldsymbol{h}_i, \boldsymbol{m}_i])\\
\boldsymbol{\tilde{h}}_i &=& \tanh{\boldsymbol{\Theta}_h[\boldsymbol{r}_i\odot \boldsymbol{h}_i, \boldsymbol{m}_i]}\\
\boldsymbol{h}_i & \leftarrow & (1-\boldsymbol{z}_i)\odot \boldsymbol{h}_i + \boldsymbol{z}_i \odot \boldsymbol{\tilde{h}}_i
\end{eqnarray}
メッセージ$\boldsymbol{m}_i$
に隣接ノードの特徴を取り込んで, GRUで計算したゲート$\boldsymbol{z}_i$にしたがって潜在ベクトルを更新します.
GCN
GCNは, CNNのようにフィルタの畳込みをグラフ上で行うことでグラフやノードの潜在ベクトルを得る方法です.
畳込みの定義の仕方にはグラフフーリエ変換を用いるアプローチとより直接的なアプローチの2種類がありますが, ここでは前者について説明します.
Spectral GCN
グラフラプラシアンの(正規化された)固有ベクトルを並べた行列$\boldsymbol{U}$を用いて, グラフ上の信号(ノードの関数)$\boldsymbol{x} \in \mathbb{R}^N$のグラフフーリエ変換$\mathcal{F}_G$は次のように与えられます.
\mathcal{F}_G[\boldsymbol{x}] = \boldsymbol{U}^{\rm{T}}\boldsymbol{x}
この式の意味については, [4]をご参照ください. やや難しい話にはなりますが, 美しい理論に支えられていることがわかります.
さて, $\boldsymbol{\mathcal{L}}$は実対称行列であったので, $\boldsymbol{U}$の各列は正規直交基底をなします. すなわち, $\boldsymbol{U}\boldsymbol{U}^{\rm{T}}=\boldsymbol{I}$が成り立ちます(記号にUを選んだのはユニタリ行列だからです).
したがって, 逆グラフフーリエ変換$\mathcal{F}_G^{-1}$は次のように導けます.
\mathcal{F}_G^{-1}[\mathcal{F}_G[\boldsymbol{x}]] = \boldsymbol{U}\boldsymbol{U}^{\rm{T}}\boldsymbol{x} = \boldsymbol{x}
時系列信号や画像の場合と同様に, 空間領域での畳込みはスペクトル領域で要素積となります.
\boldsymbol{x}_1*_G\boldsymbol{x}_2 = \mathcal{F}_G^{-1}[\mathcal{F}_G[\boldsymbol{x}_1] \odot \mathcal{F}_G[\boldsymbol{x}_2]] = \boldsymbol{U} ( (\boldsymbol{U}^{\rm{T}}\boldsymbol{x}_1) \odot (\boldsymbol{U}^{\rm{T}}\boldsymbol{x}_2) )
フィルタ$\boldsymbol{f}_{\theta} \in \mathbb{R}^N$
の畳込みは, $\boldsymbol{\Theta}=\mathrm{diag}(\boldsymbol{U}^{\rm{T}}\boldsymbol{f}_\theta) \in \mathbb{R}^{N \times N}$ とおくと簡単に表せます.
\boldsymbol{x}*_G\boldsymbol{f}_\theta = \boldsymbol{U\Theta U}^{\rm{T}}\boldsymbol{x}
グラフ上の畳込みを行列のかけ算で表すことができました. この操作を多層に重ねて, フィルタ$\boldsymbol{\Theta}$を学習することで"ディープラーニング"ができるようになります.
具体的には第$l$層でフィルタを$f_l$個用意して, それぞれを畳み込んだ結果を足しあわせて活性化関数に入れ, その出力を次の層に渡します.
\boldsymbol{x}_j^{l+1} = \rho \Biggl( \sum_{i=1}^{f_l}\boldsymbol{U}\boldsymbol{\Theta}_{i,j}^l\boldsymbol{U}^{\rm{T}}\boldsymbol{x}_i^l \Biggr),
~~~~~j=1,...,f_{l+1}
CNNと似た形になっていますが, GCNはグラフ全体にフィルタをかけているところが異なります.
以上がSpectral GCNの概要です. 理論的にはすっきりしていますが, このままでは2つの大きな欠点があります.
- $\boldsymbol{L}$の固有値分解を含むので最低でも$O(N^2)$の計算量がかかる
- 学習されるパラメータ$\boldsymbol{\Theta}$が$\boldsymbol{U}$に依存する形になっているため, 異なる構造のグラフ間で同じパラメータを利用できない
ChebNet
ChebNetは, $K$次のChebyshev多項式近似により行列の固有値分解を回避するアルゴリズムです. これによると, 学習されるパラメータは次のようになります.
\boldsymbol{\Theta} = \sum_{k=0}^{K}\theta_k \mathcal{T}_k(\boldsymbol{\tilde{\Lambda}})\\
\boldsymbol{\tilde{\Lambda}} = \frac{2}{\lambda_{max}}\boldsymbol{\Lambda} - \boldsymbol{I}
第2式では固有値が$[-1,1]$に収まるるようなスケーリングを施しています.
なお, Chebychev多項式は次の漸化式で定義されます.
\mathcal{T}_k(x) = 2x\mathcal{T}_{k-1}(x)-\mathcal{T}_{k-2}\\
\mathcal{T}_0(x)=1\\
\mathcal{T}_1(x)=x
このとき, グラフ畳込みは次のように求められます.
\boldsymbol{x}*_G\boldsymbol{f}_\theta = \boldsymbol{U}\Biggl(\sum_{k=0}^{K}\theta_k \mathcal{T}_k(\boldsymbol{\tilde{\Lambda}})\Biggr)\boldsymbol{U}^{\rm{T}}\boldsymbol{x}=\sum_{k=0}^{K}\theta_k \mathcal{T}_k(\boldsymbol{\tilde{\mathcal{L}}})\boldsymbol{x}\\
\boldsymbol{\tilde{\mathcal{L}}} = \frac{2}{\lambda_{max}}\boldsymbol{\mathcal{L}} - \boldsymbol{I}
疎行列積を使うと、この計算量は$O(KM)$に削減できます.
また, $k$のときの畳込みは距離$k$までの周辺ノードの特徴を取り込むことと対応しており, CNNのような局所的なフィルタ演算が実現されました.
GCN (Kipf+)
Kipfら[6]は, ChebNetで$K=1, \lambda_{max}=2$とした場合を考えました(単にGCNと呼ばれることがあります).
このとき, 先ほどのChebyshev多項式を陽に書くことができて,
\boldsymbol{x}*_G\boldsymbol{f}_\theta = \theta_0 \boldsymbol{x}+\theta_1 (\boldsymbol{\mathcal{L}} - \boldsymbol{I})\boldsymbol{x}\\
= \theta_0 \boldsymbol{x} - \theta_1 \boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{A}\boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{x}
となります.
さらに, $\theta = \theta_0 = -\theta_1$としてパラメータを減らします.
\boldsymbol{x}*_G\boldsymbol{f}_\theta = \theta (\boldsymbol{I} + \boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{A}\boldsymbol{D}^{- \frac{1}{2}})\boldsymbol{x}
$\boldsymbol{I} + \boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{A}\boldsymbol{D}^{- \frac{1}{2}}$の固有値は$[0,2]$の範囲に収まるのですが, このままだと計算上不安定だったり勾配消失が起きたりするそうです. そこで, $\boldsymbol{\tilde{D}}=\boldsymbol{D+I}, \boldsymbol{\tilde{A}}=\boldsymbol{A+I}$とおいて,
\boldsymbol{I} + \boldsymbol{D}^{- \frac{1}{2}}\boldsymbol{A}\boldsymbol{D}^{- \frac{1}{2}} =
\boldsymbol{\tilde{D}}^{- \frac{1}{2}}\boldsymbol{\tilde{A}}\boldsymbol{\tilde{D}}^{- \frac{1}{2}}
と置き換えるrenormalization trickを導入しました. すると, 第$l$層での計算は次のようになります. 各ノードが$f_l$次元の特徴を持つとして, $\boldsymbol{x}^l \in \mathbb{R}^N$の代わりに$\boldsymbol{H}^l \in \mathbb{R}^{N \times f_l}$を更新します.
\boldsymbol{H}^{l+1} = \rho ( \boldsymbol{\tilde{D}}^{- \frac{1}{2}}\boldsymbol{\tilde{A}}\boldsymbol{\tilde{D}}^{- \frac{1}{2}}\boldsymbol{H}^l\boldsymbol{\Theta}^l ), ~~~~~where~ \boldsymbol{\Theta}^l \in \mathbb{R}^{f_l \times f_{l+1}}
これで, Spectral GCNがSpatial GCNのアーキテクチャとつながりました.
Spatial GCNは種類がたくさんあるので, 次の記事に回します. 次回にもご期待ください!!
(次回はもう少し図をがんばりたいです)
参考文献
[1] Z. Zhang et al., Deep Learning on Graphs: A Survey, arXiv, 2018.
本記事は主にこちらの論文をベースにしています. 3本の中で一番わかりやすく感じました.
[2] J. Zhou et al., Graph Neural Networks: A Review of Methods and Applications, arXiv, 2018.
[3] Z. Wu et al., A Comprehensive Survey on Graph Neural Networks, arXiv, 2019.
[4] グラフラプラシアン - 初級Mathマニアの寝言
「$\boldsymbol{L} = \boldsymbol{D}-\boldsymbol{A}$がなぜ『ラプラシアン』と呼ばれるのか」, 「その固有ベクトルとフーリエ変換がどのようにして結びつくのか」といった疑問に明快に答えてくれるブログです. これを読んで私は感動しました.
[5] 機は熟した!グラフ構造に対するDeep Learning, Graph Convolutionのご紹介 - ABEJA Arts Blog
2年前の記事ですが, こちらも参考にしました. GCNと化学に関する内容です.
[6] T. Kipf et al., Semi-Supervised Classification with Graph Convolutional Networks, ICLR., 2017.
