概要
ベイズ推論の考え方の説明とそれを行うことのできるPythonライブラリPyMC3を使って例題を解いてみる。
例題等はこちらのリポジトリを参考にしています。
https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers
ベイズ推論の考え方
例
あなたは野クルの部員です。ある友達に一緒にキャンプに行こうと誘いました。
以下の結果が得られる時、友達が誘いにYESと言ってくれる確率はいくらでしょうか?
結果
1回目のお誘い=>NO
2回目のお誘い=>NO
3回目のお誘い=>NO
この時、頻度主義の考え方だと、友達がYESと言ってくれる確率は0/3=0%となります。
一方ベイズ的な考え方では、確率を信念の度合いで表すこととしています。
確率を「ある出来事がどれくらい信頼できるか」を示す指標と解釈することがベイズ主義です。
この例だと、「誘っている友達が一緒にキャンプしてくれることをどれくらい信頼できるか」と言い換えられます。(なので、友達がYESと言ってくれるという信念が強ければ4回目にYESと言ってくれる確率は100%と考えることもできる)
人によって信念(確率)が異なることを定義が許しているのが特徴です。
Pythonライブラリ PyMC
ベイズ推論をすることのできるPythonライブラリ。
マルコフ連鎖モンテカルロ法(MCMC)アルゴリズムを用いて値を収束させています。
Python3系のPyMC3とPython2系のPyMC2がありますが、PyMC3の方が高速で、さらに2と3ではモデルの書き方などに差異があって両方触るのは学習コストがかかるため、基本的にはPyMC3を使っておけば良いと思います。(ただし本や記事によってはPyMC2の記述しかないものもあります)
ベイズ推論の例
0から1の連続値で等確率の事前分布を0か1が50%の確率で決まる100,000個の観測値から事後分布を推論します。
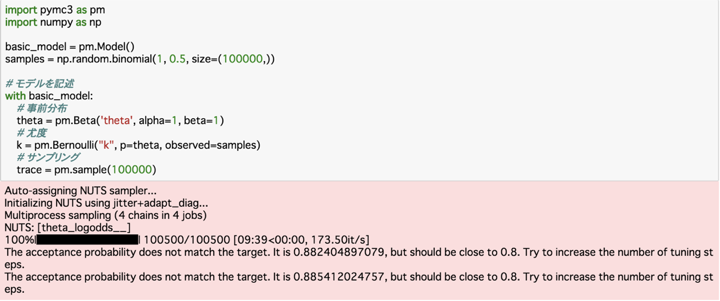
以下の画像のように、pm.Model()をインスタンス化して、Modelを定義してpm.sample()でサンプリングを行います。
この画像では100,000回サンプリングを行なっています。(約10分ほど実行に時間がかかりました)
サンプリング数による事後分布の比較
基本的にサンプリング数が多いほど正確な結果となります。
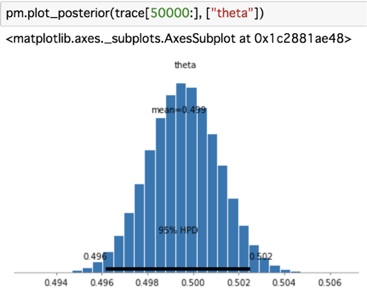
サンプル数: 100,000
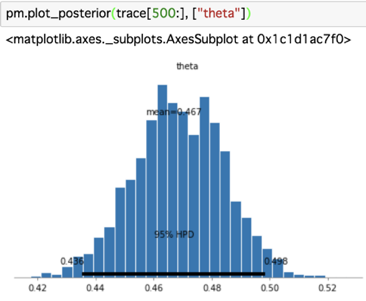
サンプル数: 1,000
このように、サンプリング数100,000回だと分布の平均が0.499と正解の50%にかなり近い値になっています。
1,000回だとかなりばらつきが目立ち、分布の平均も0.467とやや正解とは外れた値となりました。
実際の課題を解いてみよう
ベイズ推論を実際の現場でどのように使えばいいのか考えてみます。
今回はWebサービスでよく行われるABテストの結果を元に分析を行う例を取り上げます。
例題: サイトAとBどちらがよりコンバージョンに繋がる?
◯求め方
-
コンバージョンの是非で0か1の2値の観測データを用意する
-
サイトABのコンバージョン率の事前分布を決める
-
サイトABのコンバージョン率の事後分布を観測データを元にサンプリングする
-
事後分布の差を元にサイトABどちらがよりコンバージョンに繋がりそうか分析する
-
コンバージョンの是非で0か1の2値の観測データを用意する
今回は事前データを自作します。
サイトAのコンバージョン率を5%, サイトBのコンバージョン率を4%とします。(なのでこの分析の結果としてはサイトAのコンバージョン率の方が良い、という結果が得られると良い)
観測データを作成し、そのデータの平均がそれぞれ約5%と約4%であることを確認します。

2.サイトABのコンバージョン率の事前分布を決める
3.サイトABのコンバージョン率の事後分布を観測データを元にサンプリングする
今回は事前分布を0〜1の一様分布としました。
モデル化して、20,000回サンプリングを実行します。

4.事後分布の差を元にサイトABどちらがよりコンバージョンに繋がりそうか分析する
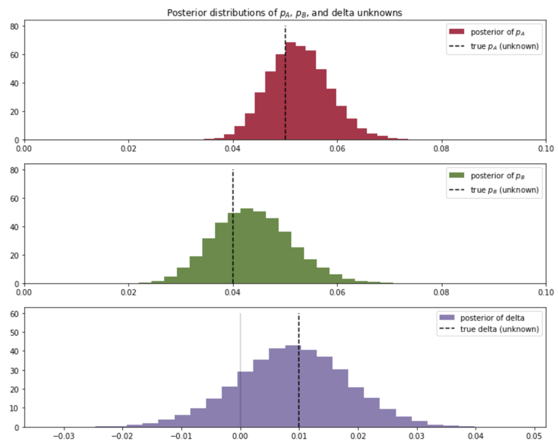
1番上のグラフがサイトAの事後分布で、正しい値である0.05に近い値の分布になっていることがわかります。
真ん中のグラフがサイトBの事後分布で、正しい値である0.04に近い値の分布になっていることがわかります。
1番下のグラフは、サイトAの事後分布-サイトBの事後分布をグラフ化したものです。
このグラフの0より小さい面積がサイトAがサイトBより悪い確率、0より大きい面積がサイトBがサイトAより悪い確率ということができます。

このように、サイトBがサイトAよりコンバージョンが悪い(サイトAよりサイトBの方がコンバージョンが良い)と83%くらいの確率で言えるという結論を得ることができました。
まとめと今後
PyMC3を用いて実際の問題の分析をすることができました。
今回は2値の事前分布のデータ分析を行いましたが、他の確率分布についてもモデル化して推論を行なっていきたいです。
