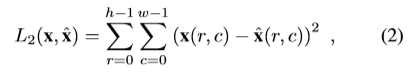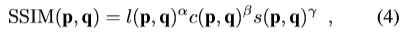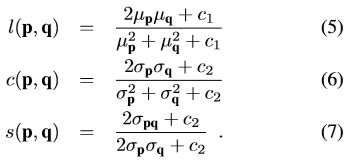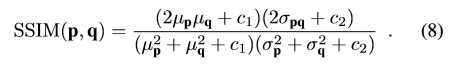以前の記事でオートエンコーダによる異常検知は古い!と書いてしまいましたが、
最近は進化しているようです。
今回ご紹介する論文は、損失関数を工夫することで通常のオートエンコーダよりも
異常検知能力を上げる手法です。
※本稿の図は論文(Improving Unsupervised Defect Segmentation by Applying Structural Similarity To Autoencoders)より引用しています。
論文の概要
- 通常のオートエンコーダによる異常検知は、微小な異常は捉えられない。
- そこで、一枚の画像に対し小さな枠を用意して「輝度」、「コントラスト」、「構造情報」の類似度を計算して異常検知を行う。
- 本手法を使うことで、通常のオートエンコーダやVAEの異常検知と比べて、AUCで大幅な向上が見られた。
- 異常部分の可視化についても、通常のオートエンコーダよりも優れていた。
オートエンコーダによる異常検知
上の図はオートエンコーダによる異常検知を説明した図です。
異常検知の手順は以下のとおりです。(上段の図を見ていただくと分かりやすいです。)
- まず、元画像をオートエンコーダに渡し、再構築画像(Reconstruction)を得ます。
- そして、再構築画像と元画像の差をとって差分画像(Residual Map)を得ます。
- 最後に差分画像で数値が大きいところを色付け(Segmentation)します。
通常のオートエンコーダによる異常検知は、損失関数が以下の式になっています。
論文では、これを$l_2-Autoencoder$と呼んでいます。
ところが、上図の上段のように可視化がうまくいっていません。
そして、後述するように異常検知のスコアも今一つといったところです。
そこで、論文ではSSIMという指標を使って損失関数を変更しています。
SSIMを使うと、上図の下段のように可視化がうまくいっています。
SSIM オートエンコーダ
SSIMは、2004年に提唱された画像の類似度を測る指標です。
いま、pとqという画像があるとしてSSIMは以下の式で与えられます。
ただし、$l$は輝度、cはコントラスト、sは構造情報です。
$l,c,s$は次で定義されます。
ここで、$\mu_p,\mu_q$は画像の平均強さ、$\sigma_p^2,\sigma_q^2$は画像の分散、$\sigma_{pq}$は画像p,qの共分散です。
パラメーターは以下の値を使っています。
\alpha=\beta=\gamma=1\\
c_1=0.01\\
c_2=0.03
まとめると、SSIMは以下の式になります。
式(8)は微分可能で、オートエンコーダの損失関数に組み込めます。
謎の後処理
ここまでは理解できたのですが、差分画像を得たあとに、SSIMでは
謎の後処理が入っています。
上図のように、差分画像の白い部分がそのまま色付けされているわけではなく、
ノイズを消してから色付けされています。論文中では以下の記載があります。
An opening with a circular structuring element of diameter 4 is applied as a morphological post-processing to delete outlier regions that are only a few pixels wide (Steger et al., 2018).
推察するに、「数ピクセルしかない異常部分を消すために直径4のフィルターの
ようなものを適用した」らしいのですが、参考文献が書籍のため、調査することが
できませんでした。(力及ばず、残念。)
実験
実験条件は以下のとおりです。
- 元画像は512 x 512で256 x 256に圧縮し、128 x 128でランダムに画像を切り取る
- 上記の手法で正常画像10000枚を採取
- SSIMを適用する画像のサイズは11 x 11
- 最適化手法はAdam(パラメーターは初期値)を使用
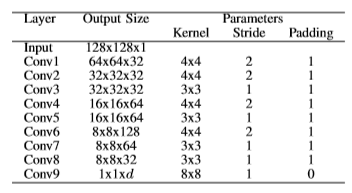
下の表は今回使用したエンコーダの構造を示しています。
デコーダはエンコーダと逆の構造です。
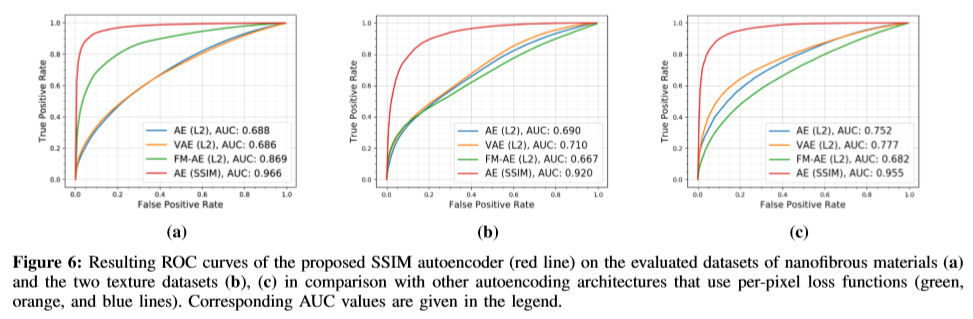
下の図は異なるデータセット(a),(b),(c)を使って異常検知したときの
AUCを示しています。
ご覧のとおり、AE(SSIM)(赤線)が圧倒的な性能を示しており、うまく機能している
ことが分かります。
下の図は異常部分の色付けを示しています。
ご覧のとおり、SSIMだと過不足なく可視化ができています。
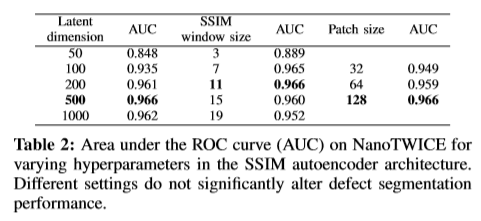
下の表はパラメータを変えたときのAUCを示しています。
パラメータ変更によるAUCの変動は少なく、パラメータの探索はあまり必要ないようです。
感想
- 可視化がきれいに行われていて現場で非常に役立ちそうです。
- 本当は、本手法を実装して「metric learningによる異常検知」と比較してみたかったのですが、謎の後処理があり断念しました。
- 論文で使われているデータセットもリンク切れになっている模様?
次回は「最新の異常検知データセット」を使って、SSIM vs metric learningの精度対決を行います。