matplotlibのplot_surfaceで100万個ほどのデータなのにメモリエラーが出たので解決策

##matplotlibで3Dのグラフを描いてみよう

matplotlibで3次元のグラフを描くのは、とりあえず
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
などを使えば、出来るとされています

特にAxes3Dクラスのメソッドであるplot_surfaceを使えば簡単に描けるというので、
早速描いてみましょう

[Pythonによる科学・技術計算] 3次元曲面の描画，サーフェス，ワイヤーフレーム，可視化，matplotlib
を真似てみて

from mpl_toolkits.mplot3d import Axes3D   
import matplotlib.pyplot as plt 
import numpy as np

fig = plt.figure() #プロット領域の作成
ax = fig.gca(projection='3d') #プロット中の軸の取得。gca は"Get Current Axes" の略。

x = np.arange(-2, 2, 0.05) # x点として[-2, 2]まで0.05刻みでサンプル
y = np.arange(-2, 2, 0.05)  # y点として[-2, 2]まで0.05刻みでサンプル
x, y = np.meshgrid(x, y)  # 上述のサンプリング点(x,y)を使ったメッシュ生成

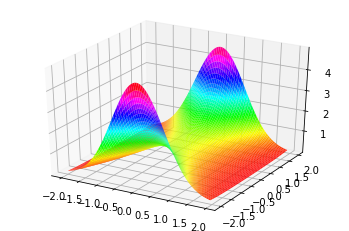
z = np.exp(-(x**2 - 0.4*(y**2)))  #exp(-(x^2-0.4*y^2))  を計算してzz座標へ格納する。

ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='hsv', linewidth=0.3) # 曲面のプロット。rstrideとcstrideはステップサイズ，cmapは彩色，linewidthは曲面のメッシュの線の太さ，をそれぞれ表す。

plt.show() # 絵の出力。

(現時点でHaru_M D氏の許可を得ていないのですが、これでいいのでしょうか？)

他の人がどう思うかはともかく、個人的には馬の鞍型の綺麗な形ができました。

#ではzの値が数式でなく数値で与えられていたらどうするか

私は
・xとyが1次元のリスト
・zが2次元のリスト、len(x)×len(y)個のデータおよびそういう構造
の3次元の点列を図にしてみようと考えました

それで、

x=[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375]
y=[-3.6, -2.8, -2.0,  -1.2, -0.4,  0.4,  1.2,  2.0,   2.8,  3.6]

というx,y座標に対して、randomにz座標を割り振ってみたらどうなるかなと思い、
Haru_M D氏の例に倣って、x,yをmeshgridで処理して何か描けばいいのかな？
と思いました

from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

import random
import time

tx=[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375]
ty=[-3.6, -2.8, -2.0,  -1.2, -0.4,  0.4,  1.2,  2.0,   2.8,  3.6]

X = np.array(tx)#numpy型に変換します

Y = np.array(ty)

print(str(len(X)) + ','+str(len(Y)))#8×10の配列であると確認しております

Z = []
tz=[]
for i in range(10):
    Z.append(tz)
    for j in range(8):         
        tz.append(random.uniform(0,3))           
    tz=[]
#ここを内包表記でスマートに書くと私はミス連発になるので泥臭くやっています
        
print(print([len(v) for v in Z])#これで配列が何×何なのか分かり易い、と聞いております
print(Z)

z_new= np.array(Z,dtype=np.float)#念のため浮動小数点にしておきます
print(z_new)

# 時間計測開始
time_sta = time.time()#何故か時間を測ります

X, Y = np.meshgrid(X, Y)#Haru_M D氏に倣って、meshgridというもので処理します

fig = plt.figure()

ax = fig.gca(projection='3d')

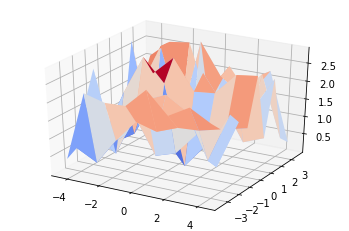
surf = ax.plot_surface(X, Y, z_new, rstride=1, cstride=1, cmap=cm.coolwarm)
#plot_surface関数の使い方はこんなもので良いのですかねえ？
plt.show()

# 時間計測終了
time_end = time.time()
# 経過時間（秒）
tim = time_end- time_sta

print(tim)#core i3 6100TのPCでも0.2秒で出力されます

(zの値がランダムなので、もちろん毎回形は違います)

これに関しては上手く行きました

#大失敗した例

(・・・普通、3次元っていったら(x,y,z)で固めとくもんだな)
(・・・それも1つ1つの座標で提示するもんだな)
(・・・なら、xもyもzと同じlen(x)×len(y)、つまりこの場合8×10にしとかないといけないのかな？)

と考えてしまいまして、

x=[[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375]]

y=[[-3.6,-3.6,-3.6,-3.6,-3.6,-3.6,-3.6,-3.6],
[-2.8,-2.8,-2.8,-2.8,-2.8,-2.8,-2.8,-2.8],
[-2.0,-2.0,-2.0,-2.0,-2.0,-2.0,-2.0,-2.0,],
[-1.2,-1.2,-1.2,-1.2,-1.2,-1.2,-1.2,-1.2],
[-0.4,-0.4,-0.4,-0.4,-0.4,-0.4,-0.4,-0.4],
[0.4,0.4,0.4,0.4,0.4,0.4,0.4,0.4],
[1.2,1.2,1.2,1.2,1.2,1.2,1.2,1.2],
[2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0],
[2.8,2.8,2.8,2.8,2.8,2.8,2.8,2.8],
[3.6,3.6,3.6,3.6,3.6,3.6,3.6,3.6]]

と、予め8×10の配列にして作ったらどうなるの？と思いました

from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import griddata

import random
import time

tX=np.arange(-5, 5, 1.25)

X=[]
for i in range(len(tX)):
    X.append(tX[i] + 0.625)#わざわざ0を中心にするためにずらしました

tY=[-3.6,-2.8,-2.0,-1.2,-0.4,0.4,1.2,2.0,2.8,3.6]
Y = np.array(tY)

print(str(len(X)) + ','+str(len(Y)))#長さは見ておきましょう

print(X)
print(Y)

Z=[]
for i in range(80):
    Z.append(random.uniform(0,3))        
print(Z)

fP=[]#まさに馬鹿正直に[[x0,y0,z0],[x1,y1,z1]・・・]と詰め込むための配列です
tf=[]
for j in range(10):
    for i in range(8):
        tf.append(X[i])
        tf.append(Y[j])
        tf.append(Z[10*i+j])
        fP.append(tf)
        tf=[]

print(print([len(v) for v in fP]))
print("使いたい配列の全体は")
print(fP)
print(fP[0][0])
print(fP[0][1])
print(fP[1][0])#苦労して配列詰め直してますが、うまく詰め込めたみたいですね
x_new=[]
y_new=[]
z_new=[]

for i in range(len(fP)):#ここでまた何故か1次元配列に並べ直しました
    x_new.append(fP[i][0])
    y_new.append(fP[i][1])
    z_new.append(fP[i][2])
    
print("x_newは")
print(x_new)
print(len(x_new))
print("y_newは")
print(y_new)
print(len(y_new))
print("z_newは")
print(z_new)
print(len(z_new))

x_np=np.array(x_new,dtype=np.float64)
y_np=np.array(y_new,dtype=np.float64)
z_np=np.array(z_new,dtype=np.float64)

X_mesh, Y_mesh = np.meshgrid(x_np, y_np)#何かmeshgridがいいみたいなんでそうします
print("meshgridを経たX_meshの形は")
print(print([len(v) for v in X_mesh]))
#meshgridを経たX_meshの形は
#[80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80]とか書いてあります
print("meshgridを経たY_meshの形は")
print(print([len(v) for v in Y_mesh]))
#meshgridを経たY_meshの形は
#[80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80]とか書いてあります

# 時間計測開始
time_sta = time.time()

fig = plt.figure()
ax = fig.gca(projection='3d')
Z_mesh = griddata((x_np, y_np),z_np,(X_mesh,Y_mesh))#後述するリンク先の方により、griddataというのがいいみたいですね？
print("griddataを経たZ_meshの形は")
print(print([len(v) for v in Z_mesh]))
#griddataを経たZ_meshの形は
#[80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80]とか書いてあります
surf = ax.plot_surface(X_mesh, Y_mesh, Z_mesh, rstride=1, cstride=1, cmap=cm.coolwarm)
plt.show()

# 時間計測終了
time_end = time.time()
# 経過時間（秒）
tim = time_end- time_sta

print(str(tim)+"秒です")

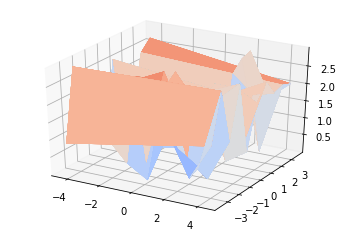
何か、全然違う形になってしまいましたよ？
時間も0.8秒くらいと、4倍も掛かっています

#どこが間違っているのか
そもそも
X_mesh, Y_mesh = np.meshgrid(x_np, y_np)
という関数で何をしているかというと、

[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375]

という横の配列を

[[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375],
[-4.375, -3.125, -1.875, -0.625, 0.625, 1.875, 3.125, 4.375]]

と、段数をyの要素数だけ増やし

[-3.6,
-2.8,
-2.0,
-1.2,
-0.4,
0.4,
1.2,
2.0,
2.8,
3.6]

という縦の配列を

[[-3.6,-3.6,-3.6,-3.6,-3.6,-3.6,-3.6,-3.6],
[-2.8,-2.8,-2.8,-2.8,-2.8,-2.8,-2.8,-2.8],
[-2.0,-2.0,-2.0,-2.0,-2.0,-2.0,-2.0,-2.0,],
[-1.2,-1.2,-1.2,-1.2,-1.2,-1.2,-1.2,-1.2],
[-0.4,-0.4,-0.4,-0.4,-0.4,-0.4,-0.4,-0.4],
[0.4,0.4,0.4,0.4,0.4,0.4,0.4,0.4],
[1.2,1.2,1.2,1.2,1.2,1.2,1.2,1.2],
[2.0,2.0,2.0,2.0,2.0,2.0,2.0,2.0],
[2.8,2.8,2.8,2.8,2.8,2.8,2.8,2.8,2.8],
[3.6,3.6,3.6,3.6,3.6,3.6,3.6,3.6,3.6]]

と、列方向にxの数だけ増やしている、そういう役割があるのです
つまり、わざわざ[[x0,y0,z0],[x1,y1,z1],・・・]なんて形にしているのだったら、
その段階でxもyも、meshgridと似たようなことをやっただけ！という事になります

そしてこの時に、meshgridされたx,yと[[x0,y0,z0],[x1,y1,z1],・・・]から取り出した
[x0,x1・・・],[y0,y1・・・]で何が違うかというと、meshgridされたものはlen(x)行len(y)列にまとまっていますが、[x0,x1・・・]は1次元に並んでいるだけなのです。

私はそれをわざわざ、np.reshape()で纏めて再び素早く描画する、というプログラムも一応書いたのですが、一体何度手間なんだと自分でもあきれ返ったので、もうそれを載せる気はありません

またzに対してgriddataという関数でまた改造していますが、これは
【Python】matplotlib の「TypeError: Input z must be a 2D array.」でお困りの方へ【3次元プロット】
という、@kzm4269氏の記事をそのまま猿真似したのが原因でした。
(現時点で@kzm4269氏の許可を得ていないのですが、これでいいのでしょうか？)
meshgridとgriddataが何をしているかを、もっとしっかり調べる必要があったのです。

###実際に私がやらかした大失態
・4桁オーダー×4桁オーダーのx,yに対するz、で3次元図形を描こうとしましたが、
表題にある通り、本来は100万個ほどの座標での処理だったのが
100万×100万=1兆(実際に10兆)個での計算になり、メモリエラーの表示が出た

・試しに40×40とか60×60で試したら、cmap=cm.coolwarmを使っていたせいもあって描画に数十分掛かり、幾らなんでもこれはおかしいと考えた

・さらにそれはサーバーにアップロードする必要があるらしかったので、こんなものを動かせないだろうとサーバー担当者との話し合いまでする事になってしまった

大恥をかきました

#まとめ

・ax.plot_surfaceは3次元図形を描画するうえで便利な関数です

・でもその引数の形を間違えると酷い目に遭います

・xとyは1次元のものをmeshgridで並べた変数,
zはlen(x) × len(y)の形の変数で素直に
ax.plot_surface(X, Y, z_new)
と入れれば、動きます

・meshgridでも、あるいは間違って使ってしまったgriddataでも
その関数を使って、変数(特に配列変数)がどんな型、どんな成分数になったのかを調べながら使いましょう

##他にこんな目に遭った方はいるのでしょうか
海外の掲示板を見ると、
Surface Plot in Python - MemoryError
というところで、2次元で密度推定をしようとして失敗した！という方がおられるようですね
10000×10000でエラーになった、と書いておられます
でも、私みたいに何も考えずにメモリオーバーになった人は、いないみたいです。