遺伝的プログラミング(GP)を用いた素数関数の探索

この記事について

結論から言うと素数関数を見つけ出すことはできません．
GPの適用例を学ぶページです．GPを知らない人は気軽にどうぞ．
続き書きました(2019)

SP2LCのとの関わり

本科4年時に参加しました．以後は参加してないです．この記事ではGPと呼ばれる手法の基礎的な適用例を解説するので，知識を広めてほしいです．

遺伝的プログラミング(Genetic Programming : GP)とは

あなたはGPを知っていますか？
GPは木構造(可変長構造)を探索するアルゴリズムです．
GPでは，入力と出力が既知であるとき，入力に対して何かを行う木構造を見つけ出すことができます．このとき，ノードやエッジの数，木の大きさに制約は存在しません(もちろん計算資源等の理由から実際には制約を設けます)．

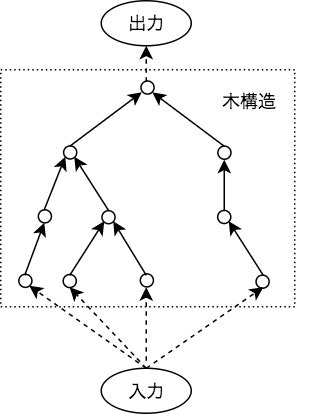
じゃあ木構造を探索すると何が美味しいの？って話になります．
世の中には木構造で表現できることは分かるけど，実際にはどんな形かわからないときがあります．今回は素数関数の例を挙げてみましょう

素数関数

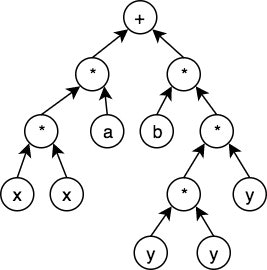
数学上では，現在のところ素数の値をとる関数は見つかっていません．ここでは，素数関数が存在すると仮定してみます．もしも，素数関数が存在するとすれば木構造で表現できます．数式(関数)が木構造で表現できるのは直感的に分かると思います．例えば

f(x,y) = ax^2+by^3

は，次の木構造で表現できます．

素数関数の入力と出力は明らかに分かる(入力：インデックスi，出力：i番目の素数)ためGPで素数関数を探索することは可能です．

i	1	2	3	4	5	6	...
P(i)	2	3	5	7	11	13	...

GPの流れ

実際のGPは次のような流れで探索を行います．実は探索過程は遺伝的アルゴリズム(GA)と全く同じです．

それぞれの処理の擬似コードは下に示します．実際のコードはGithubにあげるのでそれを見てください．

初期集団生成

初期集団生成ではN個のランダムな個体(木構造)を生成し，集団と名付けます．

initial_population

def initial_population():
  population = {}
  for i = 0 to N:
    tree = randomTreeMake()
    population = population + {tree}

評価

評価では，集団中の全ての個体に対して評価値をつけます．評価値は，木構造にインデックスiを与え，得られた出力と，P(i)の差の合計値です．要は木構造がどれだけ素数関数に近似できているかを数値化します．当然評価値は0に近づくほど真の値です．

evaluate

def evaluate():
  for tree in population:
    fitness = 0
    for i in indexs:
      fitness += |P(i)-tree(i)|
    tree.fitness = fitness

終了条件

終了条件は設定方法がいくつかありますが，今回は「評価-選択-交叉-突然変異」を1サイクル(以後1世代と呼ぶ)としたときの最大サイクル数(最大世代数)を条件にします．

termination_criteria

def termination_criteria()
  if genelation == max_Genelation:
    exit()

選択

選択では，良い個体を増やし，悪い個体を減らします．様々な選択方法が存在しますが，今回はトーナメント方法と呼ばれる選択を行います．トーナメント選択は，「ランダムに集団中から選ばれたM個の個体の内，最も良い個体を新しい集団に加える」という操作を集団の数だけ行います．

select

def select():
  new_population = {}
  for i = 0 to N:
    sub_population = randomchoice(population,M)
    best = min(sub_population)
    new_population = new_population + {best} 
  population = new_population

交叉

交叉では，集団中の2つの個体に対して，任意の部分木を交換します．このとき，交換が交叉率Pcxで行われるようにします．ここがGP(進化計算)の最も重要な解探索部分です．

crossover

def crossover():
  for i = 0 to N/2:
    if random() < Pcx:
      childA = population[2*i]
      childB = population[2*i+1]
      subtreeA = childA.subtree #select random subtree
      subtreeB = childB.subtree #select random subtree
      childA.subtree = subtreeB
      childB.subtree = subtreeA

突然変異

突然変異では，集団中の個体の任意の部分木を任意の部分木に置換します．このとき置換が突然変異率Pmutで行われるようにします．同じ個体同士の交叉では同じ個体が生まれやすいので，個体を少し変化させます．

mutation

def mutation():
  for tree in population:
    if random() < Pmut:
      new_sub_tree = randomTreeMake()
      tree.subtree = new_sub_tree #select random subtree

GPで素数関数と探索してみる

実際に素数関数を探索してみます．
使ったソースコードはこちらになります(Python3, numpy, matplotlib環境)．
https://github.com/shinjikato/gp_prime/tree/master
GPは有名なPythonの進化計算ライブラリDeapにもあるので，自分で書くときはそこを参考にすればいいと思います．Deapさんはこちら
https://github.com/DEAP/deap
実行パラメータは

• シード値 2017
• 集団サイズ　200
• 世代数 100
• 交叉率 0.5
• 突然変異率 0.1
• 素数関数の範囲 1~9まで
• ノード集合 : {add,sub,mul,div,sin,cos,tan,log,exp,sqrt}
• 葉ノード集合 : {-1,0,1,0.5,0.1,pi,e,x}

また，木の大きさに制約を設けないとコンピュータがぶっ壊れる可能性があるので，今回は木の最大の深さを17に設定しています(この値はGPの考案者が提案している値です)．

そして，最終世代で最も良かった木構造がこちらです．
add(sub(tan(x),sin(0)),add(div(sub(sub(add(div(sub(add(div(sub(sub(tan(tan(x)),div(x,div(sub(sub(tan(x),1),sqrt(1)),tan(x)))),sin(0)),pi),sub(tan(x),1)),sin(exp(div(sub(sub(tan(x),1),sqrt(1)),tan(x))))),pi),sub(tan(sub(tan(sub(sub(tan(x),div(sub(tan(x),div(x,tan(x))),tan(x))),sin(0))),exp(div(sub(sub(tan(x),1),sqrt(1)),sub(tan(x),div(sub(tan(x),div(div(x,tan(x)),tan(x))),tan(x))))))),exp(div(sub(sub(tan(x),1),sqrt(1)),tan(x))))),sqrt(1)),sqrt(1)),sin(e)),sub(add(div(sub(sub(sub(add(div(sub(sub(tan(x),div(sub(tan(x),div(x,tan(x))),tan(x))),sin(0)),pi),sub(add(div(tan(x),cos(e)),sub(tan(x),exp(sin(0.5)))),sqrt(1))),sqrt(1)),1),sin(0)),cos(e)),sub(x,exp(sin(sqrt(div(sub(sub(tan(x),1),sqrt(add(1,0.1))),tan(x))))))),sqrt(div(x,tan(x))))))
うぇ...数学の式に直すとこうなります(数式変換のプログラムを書くのが一番時間かかった)．

tan(x)-sin(0)+\frac{\frac{\frac{tan(tan(x))}{-(\frac{x}{\frac{tan(x)}{-(1)}})}}{-(\sqrt{1})}}{tan(x)}-sin(0)\pi+(tan(x))-1-sin(exp(\frac{tan(x)}{-(1)}))-\sqrt{1}tanx\pi+(tan(tan(tan(x))))\\
-\frac{tan(x)}{-(\frac{x}{tan(x)})}tanx-sin(0)-exp(\frac{tan(x)}{-(1)})-\sqrt{1}tanx-\frac{tan(x)}{-(\frac{\frac{x}{tan(x)}}{tan(x)})}tanx\\
-exp(\frac{tan(x)}{-(1)})-\sqrt{1}tanx-\sqrt{1}-\sqrt{1}sine+\frac{\frac{tan(x)}{-(\frac{tan(x)}{-(\frac{x}{tan(x)})})}}{tan(x)}-sin(0)\pi+(\frac{tan(x)}{cos(e)})\\
+tan(x)-exp(sin(0.5))-\sqrt{1}-\sqrt{1}-1-sin(0)cose+x-exp(sin(\sqrt{\frac{tan(x)}{-(1)}}))-\sqrt{1}+0.1tanx-\sqrt{\frac{x}{tan(x)}}

少しはわかりやすくなった気がします．また，この式をグラフにすると次のようになります．

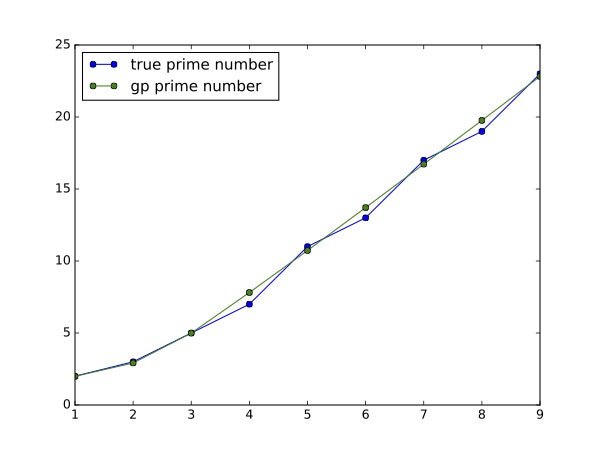
まぁあんまり近似できてないですね．実際，評価値(誤差)は3.11282242386もあります．
また，今回プログラム上での割り算はzero divide errorを防ぐためにn/0=1にしてありますから，数学上のグラフは異なる可能性があります．

他のGPの利用法

素数関数は見つけることができませんでしたが，GPは他の利用法もあります．基本的に木構造・ネットワーク構造で表現で解が表現できる最適化問題は全部解くことができます．例えば

• プログラム
  • 特定の動作をしてほしいプログラムを作り上げることができます．プログラムはフローチャートに変換できるので，要は木構造みたいなもんです．有名な問題はAnt問題と呼ばれています
• 回路
  • 論理・電子回路ともに木構造もしくはネットワーク構造で表現できるのでGPの適用範囲でしょう
• 株価・為替
  • 株価・為替の予想線もGPで解く例があったりします
• 画像処理
  • これは自分の卒研でやったのですが，画像処理の組み合わせを最適化することで，画像処理に知識がなくても、必要な処理を生み出すことができます．

こんなところですかね．それぞれ，実際にやってみると面白いともいますまぁGPは探索性能がいまいちなので，どれをやってもあんまりうまくいかないのですけど．　この性能を上げるための研究は色々提案されているんですけど，いまいち捗ってない感があります．もしも探索性能を上げる案を思いついた人は教えてください．待ってます．

おわりに

　GPの紹介はここで終わりです．柔軟な解表現ができる進化計算の中でもさらに柔軟な解表現ができるGPはどうでしたか？．今回は，素数関数をGPで見つけることはできませんでしたが，GPの良いところは，中身の木構造(式)が分かることころです．これが，CNNとかで近似線を求めると近似できても中身の関数がわかりません．もしもレポート・課題等で近似曲線とその式を求めたいときにはGPを使ってみてはどうでしょうか(非線形最小二乗法使った方が精度良さそう)

参考文献

だいたいDeapを見れば事足りる．一応GPの教科書がネットで見れるので貼っとく．
Deap
https://github.com/DEAP/deap
https://deap.readthedocs.io/en/master/
Wilipedia
https://www.wikiwand.com/ja/%E9%81%BA%E4%BC%9D%E7%9A%84%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0
A Field Guid to Genetic Programming
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.449.8986&rep=rep1&type=pdf