はじめに
Genetic Programmingを使って素数関数を発見してみようと思います.
結果から言うと発見できてないです.
前回
じつは2年前に同じ内容の記事を載せてます.
今回の記事は,前回からの2年間で学んできたGPの手法を取り入れたものとなります.
今回
前回からの差分は大きく分けて2つになります.
- Batch Tournament Selectionへの移行
- 計算機の性能向上
- scikit-learnベースの実装
前回から,Batch Tournamentと呼ばれるMini Batchの概念を取り入れたTournament Selectionを導入したことで,初期収束がなくなり,性能が飛躍的に向上しました.また,計算機の性能が向上したことで,集団サイズや世代数を増やせたので,それも性能向上に貢献しました.
GPで素数関数を探索しようとすると,学習するデータ数(素数の数)が100を超えると,ぜんぜん学習してくれません(MAE誤差が1000とかの状況が続く).そのため,前回の素数関数探索では,データ数を10にしていました.それが,今回の記事では性能向上によって,学習データをかなり多めにとれるようになりました.
実装
ソースコードはここ
scikit-learnベースで実装しましたので,fit,score,predictなどの関数が実装されています.
また,scikit-learnのcross-validationやgrid-searchなどの関数にも適用できるモデルとなっています.
実験設定
パラメータは基本的に適当に決めました.
- population size : 1000
- max generation : 1000'
- crossover : subtree swap
- crossover rate : 0.8
- mutation : node change
- mutation rate : 0.1
- height limit : 18
- selection : batch tournament
- tournament size : 64
- batch size : 8
- node set : $+,-,\times,\div,\sin,\cos,\tan,\log,\exp,\sqrt{n}$
- leaf set : $\pi,e,x$
本当は,scikit-learnベースで実装したのでgrid-searchしたほうがいいんでしょうけど,計算資源を割り当てる時間がないので,やりませんでした.誰かparameter-searchしたら,もっといい結果報告してほしい.
データですが,2から始まる2000個の素数に対して学習をします.
そのあと,2から始まる10000個の素数に対してテストしてみます.
また,素数に対するインデックスは1から始まることにします.
結果
とりあえず,作れた関数から
- e^{2} + \left(e + x\right) \log{\left (\pi \right )} \log{\left (x \right )} \cos{\left (e^{- e} \cos{\left (e e \left(\log{\left (\pi \right )} \log{\left (x \right )} - \sqrt{\pi}\right) \right )} \right )} \cos{\left (e^{- e} \cos{\left (e \sqrt{\pi} e \log{\left (\pi \right )} \log{\left (e + x + \log{\left (x \right )} \right )} \right )} \right )} - \frac{e^{- \frac{1}{e} \left(\log{\left (\pi \right )} \log{\left (x \right )} + \log{\left (\log{\left (x \right )} \right )} - \cos{\left (e e^{2} \left(e + \log{\left (x \right )}\right) \log{\left (\pi \right )} \right )}\right)} \cos{\left (\frac{1}{\cos{\left (\cos{\left (\frac{e \cos{\left (\log{\left (x \right )} \right )}}{\pi \sqrt{\cos{\left (\cos{\left (x e^{- e} \right )} \right )}}} \right )} \right )}} \cos{\left (\left(\cos{\left (e \pi \log{\left (\pi \right )} \log^{\frac{3}{2}}{\left (x \right )} \right )} - \log{\left (\pi \right )}\right) e^{- \frac{\sqrt{\pi} e \log{\left (e \right )}}{\log{\left (\pi \right )}} \left(- \pi \sqrt{e} \cos{\left (e e^{e} \sqrt{e^{\cos{\left (\log{\left (e \right )} \right )}}} e^{- \cos{\left (\log{\left (e + x \right )} \right )}} \right )} + \pi\right)} \right )} \right )}}{- e + \frac{\cos{\left (\frac{\cos{\left (e^{-1} \right )}}{\log{\left (\pi \right )}} e^{- \cos{\left (\cos{\left (\frac{\log{\left (x \right )}}{\pi \left(- \pi + \sqrt{\pi}\right)} \right )} \right )}} \sqrt{\log{\left (x + e^{\log{\left (\pi \right )} \log{\left (x \right )}} \right )}} \right )}}{\sqrt{e^{\cos{\left (\cos{\left (\frac{\log{\left (x \right )}}{\pi \left(\log{\left (\pi \right )} \log{\left (x \right )} - \pi\right)} \right )} \right )}}}} \left(- e \cos{\left (\log{\left (\pi \right )} \log{\left (x \right )} \right )} + e\right)}
ながすぎますね.sympyで簡単化をしてみたのですが,あんまり簡単にはなりませんでした.
\frac{1}{e \left(\left(\cos{\left (\log{\left (\pi \right )} \log{\left (x \right )} \right )} - 1\right) \cos{\left (\frac{\cos{\left (e^{-1} \right )}}{\log{\left (\pi \right )}} e^{- \cos{\left (\cos{\left (\frac{\log{\left (x \right )}}{- \pi^{2} + \pi^{\frac{3}{2}}} \right )} \right )}} \sqrt{\log{\left (x + e^{\log{\left (\pi \right )} \log{\left (x \right )}} \right )}} \right )} + \sqrt{e^{\cos{\left (\cos{\left (\frac{\log{\left (x \right )}}{\pi \left(\log{\left (\pi \right )} \log{\left (x \right )} - \pi\right)} \right )} \right )}}}\right)} \left(e \left(- e^{2} + \left(e + x\right) \log{\left (\pi \right )} \log{\left (x \right )} \cos{\left (e^{- e} \cos{\left (e e \left(\log{\left (\pi \right )} \log{\left (x \right )} - \sqrt{\pi}\right) \right )} \right )} \cos{\left (e^{- e} \cos{\left (e \sqrt{\pi} e \log{\left (\pi \right )} \log{\left (e + x + \log{\left (x \right )} \right )} \right )} \right )}\right) \left(\left(\cos{\left (\log{\left (\pi \right )} \log{\left (x \right )} \right )} - 1\right) \cos{\left (\frac{\cos{\left (e^{-1} \right )}}{\log{\left (\pi \right )}} e^{- \cos{\left (\cos{\left (\frac{\log{\left (x \right )}}{- \pi^{2} + \pi^{\frac{3}{2}}} \right )} \right )}} \sqrt{\log{\left (x + e^{\log{\left (\pi \right )} \log{\left (x \right )}} \right )}} \right )} + \sqrt{e^{\cos{\left (\cos{\left (\frac{\log{\left (x \right )}}{\pi \left(\log{\left (\pi \right )} \log{\left (x \right )} - \pi\right)} \right )} \right )}}}\right) + e^{\frac{1}{e} \left(- \log{\left (\pi \right )} \log{\left (x \right )} - \log{\left (\log{\left (x \right )} \right )} + \cos{\left (e e^{2} \left(e + \log{\left (x \right )}\right) \log{\left (\pi \right )} \right )}\right)} \sqrt{e^{\cos{\left (\cos{\left (\frac{\log{\left (x \right )}}{\pi \left(\log{\left (\pi \right )} \log{\left (x \right )} - \pi\right)} \right )} \right )}}} \cos{\left (\frac{1}{\cos{\left (\cos{\left (\frac{e \cos{\left (\log{\left (x \right )} \right )}}{\pi \sqrt{\cos{\left (\cos{\left (x e^{- e} \right )} \right )}}} \right )} \right )}} \cos{\left (\left(\cos{\left (e \pi \log{\left (\pi \right )} \log^{\frac{3}{2}}{\left (x \right )} \right )} - \log{\left (\pi \right )}\right) e^{\frac{\pi^{\frac{3}{2}} e \log{\left (e \right )}}{\log{\left (\pi \right )}} \left(\sqrt{e} \cos{\left (e e^{e - \cos{\left (\log{\left (e + x \right )}
\right )}} \sqrt{e^{\cos{\left (\log{\left (e \right )} \right )}}} \right )} - 1\right)} \right )} \right )}\right)
まぁ,機械学習と比べたときのGPの利点は数式で近似関数が得られることなので,良いとしましょう.
今回の関数のMAE誤差は9.479829でした.
テストデータのMAE誤差は190.50854674519です.
誤差が大きすぎますね.頑張って1以下に収めたいところ
そして,今回の求められた素数関数の曲線は次のような感じです.
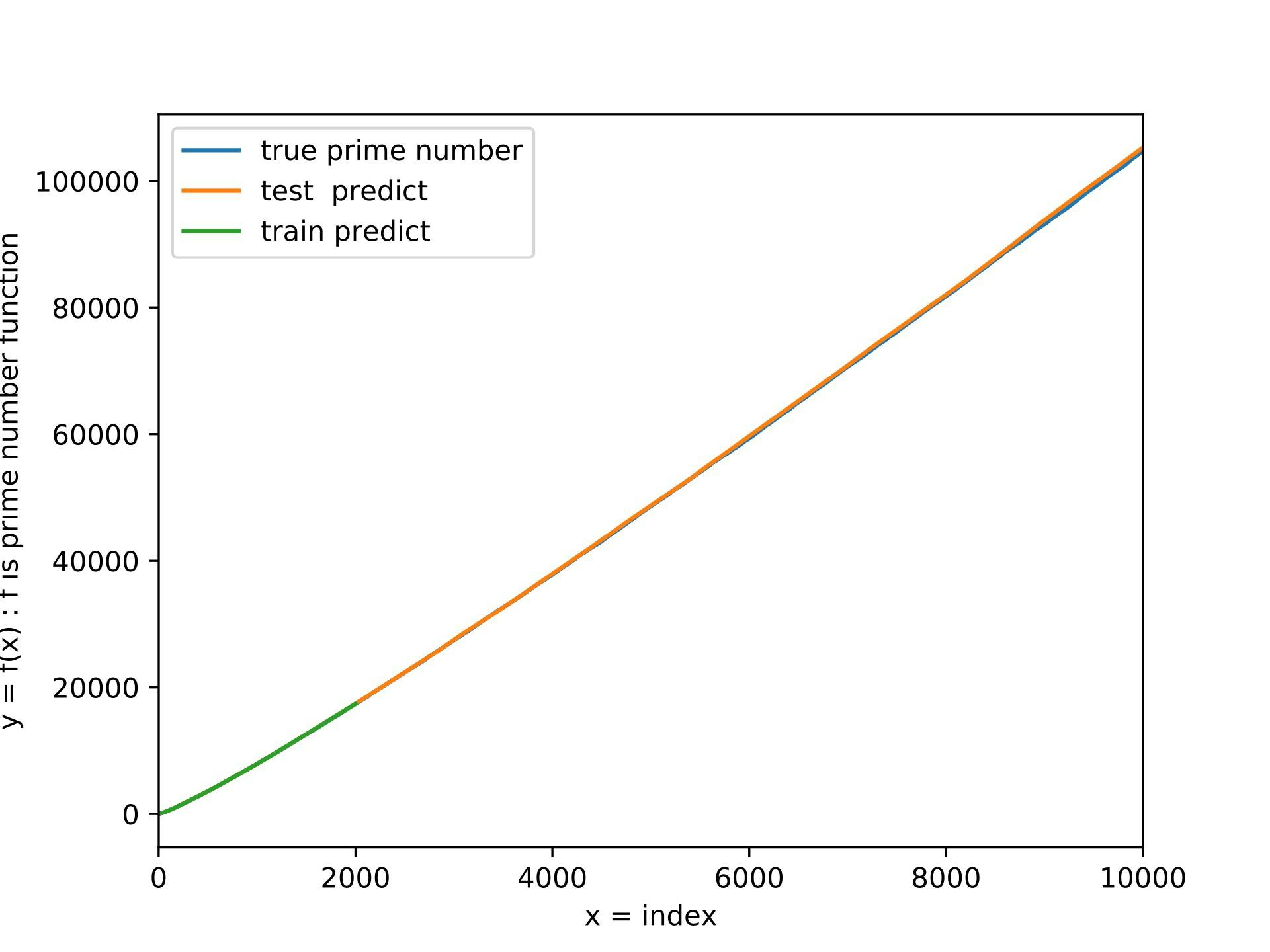
雰囲気で見ると,けっこう学習できてそうですが,誤差は190程度あるので,近似できてないです.
おわりに
本記事では,Genetic Programmingを使って素数関数を求めました.
2年前よりはいい結果が得られましたが,まだまだ素数関数を見つけることはできませんでした.
いつの日か誤差1以下の素数関数を見つけてみたいです.