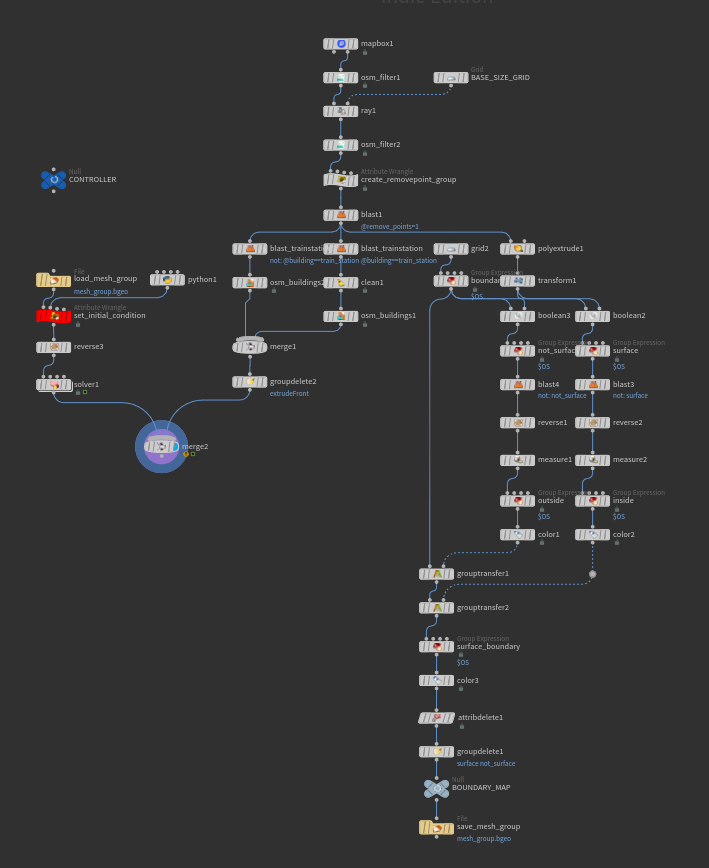
Houdini Apprentice Advent Calendar 2020、22日目の記事。
そういえば最近記事を書いていなかったなと思い今年も参加することにした。
Houdiniといえば多種多様、流体に限ったとしてもハイクオリティなシミュレーションが膨大に実装されており敢えて自前の流体計算に触れる意味は全くないわけだが、、、
大学の専門講義以来ひさびさにこの辺に触れる機会があったので、当時プログラミングが解らずに投げだした数値流体計算をあえてWrangleメインで実装してみようと思った次第。要はシミュレーションを使ってみた、ではなく作ってみた記事。
おお勇者よ、敢えて偉人の残した機能を使わず自前で劣化版を手掛けようとは情けない。
ということでこの記事、いったい誰に需要があるのかは全くわからない。
完成形:何が出来上がったのか
こんなの。
**先に述べておくが、この記事ではこのシーンの実装までは説明しない。**本来はそこまでの記事の予定だったが、前提箇所の説明で8,000字を越えてしまったため断念。
緯度・経度を引数として試しに代々木駅周辺の建物情報をMapBox$\tiny{※1}$で取得し、同一の引数でOpenWeatherMap$\tiny{※2}$からその地点の現在の風速を取得し初期条件として2次元平面で気流シミュレーション!としたかった。
ここまでいってやっとプロシージャルの効果が発揮できるわけだが・・・計算精度は粗いし、本来考慮すべき事象(方程式の項)も幾つか排除しているのでご覧の通り流体の挙動(建造物を避けたことによる流れの混雑とか回り込みとか)は正しく表現できていない。。時間なかった。。
ただまぁそこまで考慮すると大学の講義半年分くらいのボリュームになるので今回はここら辺でやめておこうかなと。実装すべき項まで盛り込んでから別途記事を書こうと思う。
※1 MapBox
今回は緯度, 経度の値を基に特定領域のMapデータをMapBoxノードで取得し、以後OSM関連のノード1で整理している。
※2 OpenWeatherMap
幾つかある気象情報配信APIの中の1つ。
緯度, 経度を引数として各種気象情報が取得できる2が今回はその地点の風速/風向のみ取得する関数をHoudini内Pythonで記述している。
前提編:知っておきたい知識
CFDとは
CFDに関しては理論/実装ともに多くの先人たちに事例を残して頂いているので、敢えて自分の感覚的な理解を文字に落とし込んでみる(というか説明の厳密さに自信がない)(あったら研究の道に進んでた)。
流れのシミュレーションは一般に数値流体力学、ないしCFD(Computed Fluid Dynamic)と呼ばれる。流体運動を記述する数学モデルである「支配方程式」の数値解を求めること…みたいな話なのだがこの辺はとても解りやすいQiita記事3がある。
数値解を求めるとは
流れを支配する方程式としてナビエ・ストークス(Navier-Stokes)方程式が知られているが、紙面にゴリゴリ書き殴って解析的に解くのはあまりにも無理ゲー4。
・・・ということで 方程式を時間方向/空間方向に離散化し、微小時間後の状態を現在のパラメータで表現してステップ式に加算していくループ計算をコンピュータにやらせてしまえ、 というのが数値流体力学の基本的なアプローチ。(面積を求めるときに微小幅dxの長方形f(x)dxに分割して、その足し合わせと考えるアレと似た感じ)
ただ「流れ」の方程式には多種の現象が加味されていて、離散化するにも複雑すぎたり計算量が膨大になったり、項として加味したからといって正確に再現されなかったり…等々の背景で、一部の項を排除して簡略化した流れのシミュレーションを実装することが少なからずある。
用いる言語は
講義で学んだのは8,9年前だったが、その時点その界隈ではまだFORTRANが主流だったように記憶している。C言語に変換する人とFORTRAN知識を詰め込む人に分かれていたのだったような…?
今でこそPythonで数値流体を実装する本5を当時の教授が出していたりして、この辺りの参考文献もだいぶ充実してきているように見える。・・・繰り返しになるがそんな中で敢えてVEXで実装してみることに意味は全くない。完全な思いつき。
方程式の簡略化とは
同一の方程式でも変数の置き方や次元の数や軸の取り方、演算子の書き方で無限にパターンが出てくるわけだが、、
例えば下記のナビエ・ストークス方程式があったとして、
\begin{eqnarray}
\rho \frac{\partial \boldsymbol{u}}{\partial t} + \rho({\boldsymbol{u}} \cdot \nabla)\boldsymbol{u}
&=& -\nabla p + \nabla \cdot \boldsymbol{T}_\nu + \boldsymbol{F} _B \tag{1}\\
&=& -\nabla p + \mu \nabla^2 \boldsymbol{u} + (\mu + \lambda)\nabla(\nabla \cdot \boldsymbol{u}) + \boldsymbol{F} _B \tag{2}
\end{eqnarray}
これを「非圧縮の流体」を仮定するなら
(流速が早くなるほど空気が圧縮される効果が無視できなくなる)
(台風くらいまでの速度なら非圧縮性流と考えてよかったはず)
\begin{eqnarray}
\rho \frac{\partial \boldsymbol{u}}{\partial t} + \rho({\boldsymbol{u}} \cdot \nabla)\boldsymbol{u}
&=& -\nabla p + \mu \nabla^2 \boldsymbol{u} + \boldsymbol{F} _B \tag{3}
\end{eqnarray}
外力ナシ、また単位体積当たりの挙動を考えるなら
\begin{eqnarray}
\frac{\partial \boldsymbol{u}}{\partial t} + ({\boldsymbol{u}} \cdot \nabla)\boldsymbol{u}
&=& -\nabla p + \mu \nabla^2 \boldsymbol{u} \tag{4}
\end{eqnarray}
等といったイメージ。つまりは汎用的な方程式ほど厳密に現象を表現できるが、(解析的にも数値的にも)解くのが難しくなる。
項をそぎ落としてスリムにした方程式ほど解く難易度は下がるが、限られたシチュエーションにしか適用できなかったり現象をざっくりとしか表現できなかったりする。
(さらに数値計算については現象に適した離散化や座標の取り方をしないとさらに精度が落ちる)
中には特定の項を落として別の名称がついている方程式も幾つかある。
※オイラー表現/ラグランジュ表現については今は考えない。迷走する。
離散化とは
時間の離散化
流体の話からは離れてしまうが、説明として使いやすいのでボールの放物運動を取り上げる。
中学理科?とか高校物理の最初辺りで扱うやつ。この辺りの導入は参考文献3を参照している。
\begin{eqnarray}
\begin{bmatrix}
x \\
y \\
\end{bmatrix}
=
\begin{bmatrix}
v_0 \cos \theta \cdot t \\
\displaystyle -\frac{1}{2}gt^2 + v_0 \sin \theta \cdot t \\
\end{bmatrix} \tag{5}
\end{eqnarray}
これを両辺tで微分して
\begin{eqnarray}
\begin{bmatrix}
\displaystyle \frac{dx}{dt} \\
\displaystyle \frac{dy}{dt} \\
\end{bmatrix}
=
\begin{bmatrix}
v_0 \cos \theta \\
\displaystyle -gt + v_0 \sin \theta \\
\end{bmatrix} \tag{6}
\end{eqnarray}
たとえばこの$\displaystyle \frac{dy}{dt}$(微小時間dtに於けるy軸方向の変化量dy)を有限量$\Delta$t、$\Delta$yで近似すると2番目の式は
\Delta y = (-gt + v_0 \sin \theta )\Delta t \tag{7}
言い換えると
y_{ちょっと後} = y_{いま} + (-gt + v_0 \sin \theta )\Delta t \tag{8}
と書けるので、SOP Solver内でこれをWrangleに記述し1フレーム=$\Delta$t(でなくてもよいが)と考えてタイムライン更新をすれば放物運動を再現できるのでは?といった次第。実装は後ほど行う。
空間の離散化
上の時間離散化の箇所でしれっと書いていた
\displaystyle \frac{dy}{dt} → \frac{\Delta y}{\Delta t} = \frac{y_{ちょっと後} - y_{いま}}{\Delta t} \tag{9}
の近似は数ある離散化手法の中でも有限差分法と呼ばれる手法になるが、この辺りも沼が深いのでWikipedia6 7を始めとした諸文献を参照のこと。
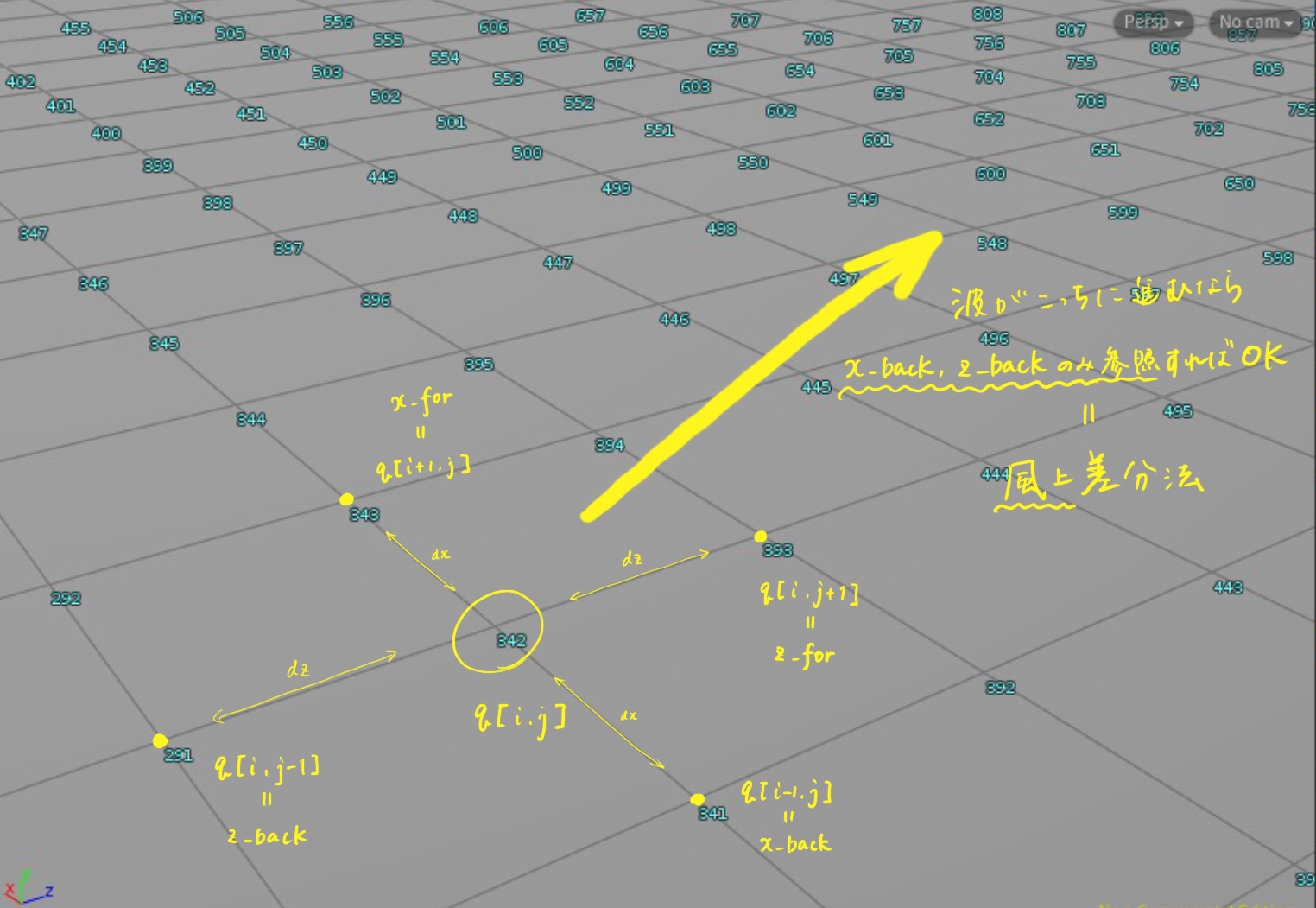
時間は(少なくとも我々が認知している世界に於いては)一方向に流れるが、殊流体に於いては 空間を格子に分解し、偏微分方程式を「隣接するセルとの関係式」に落とし込むという手法 がよく取られる。
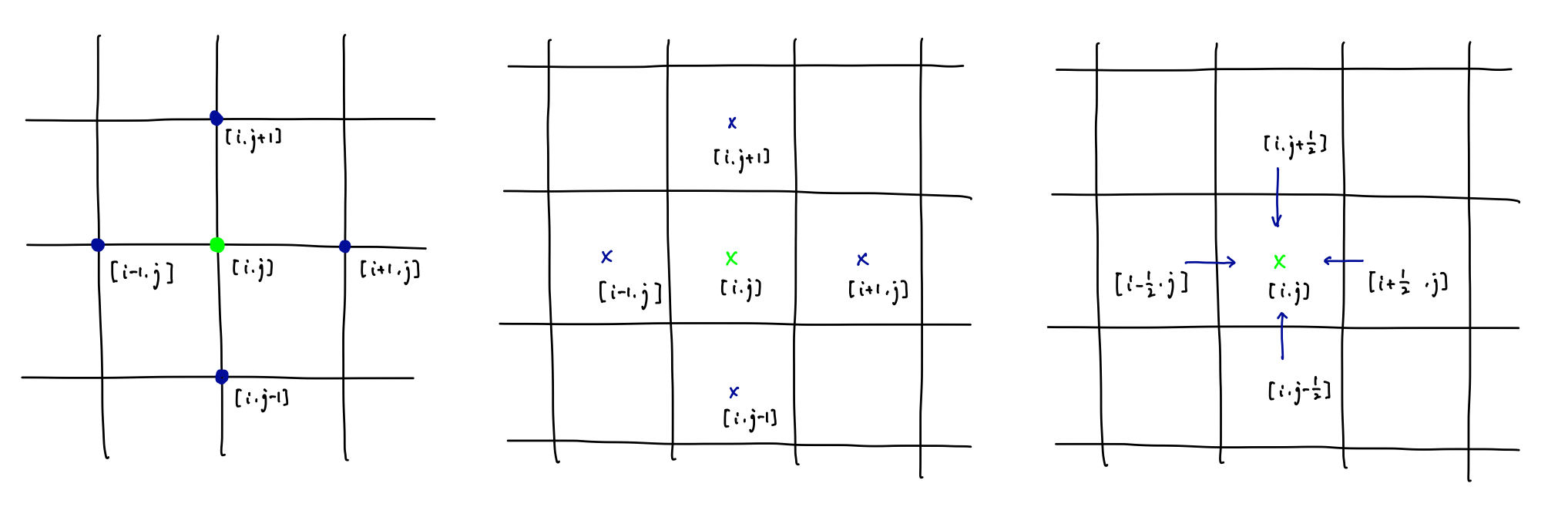
一例としては下記のようなイメージ。
どこ(点/面/…)で値を持つか、どの手法を適用するか、どういう現象をモデル化するか、…などで用いられるものも変わってくる。ちょっとHoudiniのpoint, primitive, attributeっぽくなってきた。
\color{limegreen}{p_{i, j}} = f(\color{blue}{p_{i-1, j}, p_{i+1, j}, p_{i, j-1}, p_{i, j+1}}) \tag{10}
とか
\color{limegreen}{p_{i, j}} = f(\color{blue}{q_{i-\frac{1}{2}, j}, q_{i+\frac{1}{2}, j}, q_{i, j-\frac{1}{2}}, q_{i, j+\frac{1}{2}}}) \tag{11}
みたいなイメージ。これをどうやってVEXで実現するかは後述。
準備編:この記事でどこまで扱おうか
めちゃくちゃ端折ったのにそれでも前提だけでけっこうなボリュームになってしまった。。
方程式の簡略化とは の項で出てきたナビエ・ストークス方程式、なんだかようわからん記号が並んでいるな~という感じだが、一応項ごとに意味(表す物理現象)がある。
式(4)を説明用に変形すると
\begin{eqnarray}
\frac{\partial \boldsymbol{u}}{\partial t} = -({\boldsymbol{u}} \cdot \nabla)\boldsymbol{u}
-\nabla p + \mu \nabla^2 \boldsymbol{u} \tag{4'}
\end{eqnarray}
となるが、右辺第1項は移流項、第2項は圧力項、第3項は拡散項と呼ばれる。
- 左辺:流体の時間変化
- 右辺:移流+圧力変動+拡散現象による流入/流出
が釣り合っているという見方である。
要は こんだけ簡略化しても最低限、移流・圧力・拡散の3現象をプログラムに落とし込めないと流れがシミュレーションできない って話である。まだまだフクザツ。
移流項
というわけでやっと・・・
移流項と呼ばれる元ネタである?ところの移流方程式を今回実装対象の1つ目とする。
ある物理量$q(t, \boldsymbol{r})$が速度$c$で移動することを表す移流方程式は
\frac{\partial q}{\partial t} + \boldsymbol{c}\frac{\partial q}{\partial \boldsymbol{r}} = 0 \tag{12}
これを$q$がスカラー値の場合(流体とは結びつけにくいが練習問題として)と2次元の場合(流速ベクトル=$(u, v)$という2次元平面に於ける流れのイメージ)について、かつ$\boldsymbol{r}$が2次元の場合について実装する。
拡散項
そしてもう1つは拡散項の元とされる拡散方程式を実装対象の2つ目とする。
ある物理量$q(t, \boldsymbol{r})$が係数$D$(定数とする)に従い拡散する場合の拡散方程式は
\frac{\partial q}{\partial t} = D\frac{\partial^2 q}{\partial \boldsymbol{r}^2} \tag{13}
これを$q$がスカラー値の場合(これも流体とは結びつけにくいが)について、かつ$\boldsymbol{r}$が2次元の場合について実装することにする。
本当はこれらを基に仮の速度を求め、圧力項を計算したあとに次ステップの速度をアップデートする・・・のを全セル(格子)について一斉に計算することで最低限の流れのシミュレーションが完成するわけだが、ここから先がハードすぎるので 何が出来上がったのか で言及した通り今回はこの辺にしておきたい。
記述編:実装してみる
実行環境
OS : Windows 10
Houdini : Houdini Apprentice 18.5.398
Python : 2.7.15 (記事掲載範囲内では利用なし)
hipファイル
以後で説明する内容をひとまとめにしたもの。
記事用にノードを幾つか名称変更したので齟齬あればお許しを。
vex_cfd.hipnc
[肩慣らし] 放物運動
方程式
流れのシミュレーションに入る前に、Houdiniで方程式の時間差分の実装について一例を示す。
ボールを原点から初速$v_{0}$ = 100[m/s]、水平面となす角度$\theta = $ 60[deg]方向に投げる放物運動を考える。
式(8)をx, yについて書き直すと
\begin{eqnarray}
\begin{bmatrix}
x_{ちょっと後} \\
y_{ちょっと後} \\
\end{bmatrix}
=
\begin{bmatrix}
x_{いま} + ( v_0 \cos \theta )\Delta t \\
y_{いま} + ( -gt + v_0 \sin \theta )\Delta t \\
\end{bmatrix} \tag{8'}
\end{eqnarray}
実装内容
これをSolver内attribute wrangleに書き下してみる。
Δt = 1とすることで、t = @Frameと置き換えられる。
# attribute wrangle内
float g = 9.8;
float v0 = 100;
float theta = PI/3;
@P.x += v0 * cos(theta);
@P.y += (-g * @Frame + v0 * sin(theta));
実行結果
実行結果はこんな感じ(ウィンドウ内に収まるようにパラメータ弄った)。
移流方程式
qがスカラー値の場合
方程式
ここからが本題、物理量qがスカラー値(=1次元量)でrが2次元の場合を考える。つまり
\frac{\partial q}{\partial t} + \boldsymbol{c}\frac{\partial q}{\partial \boldsymbol{r}} = \frac{\partial q}{\partial t} + c_{x} \frac{\partial q}{\partial x} + c_{z} \frac{\partial q}{\partial z} = 0 \tag{12'}
繰り返しになるが、この事例も直接流れのシミュレーションとは関係ない。
ただいきなりqもrも2次元にすると一気にフクザツになるのでステップを踏む意味で経由する。
(HoudiniがY-upなので紛らわしいが)海の波の伝播などを考えるとイメージしやすい。
放物運動でいう@Frameに当たる実行ステップ数をnで置き換え、かつx, z方向をgridに割ってそれぞれ(i, j)番地で置き換えることで
y = q(t, \boldsymbol{r}) = q(t, \boldsymbol{r}(x, z)) → q^{n}_{i, j} \tag{14}
と表現することにする。
式(12')の各項をこの表現で書き直して、
\frac{\partial q}{\partial t} → \frac{q^{n+1}_{i, j} - q^{n}_{i, j}}{\Delta t} \tag{12'-1}
c_{x} \frac{\partial q}{\partial x} → c_{x} \frac{q^{n}_{i, j} - q^{n}_{i-1, j}}{\Delta x} \tag{12'-2}
c_{z} \frac{\partial q}{\partial z} → c_{z} \frac{q^{n}_{i, j} - q^{n}_{i, j-1}}{\Delta z} \tag{12'-3}
とするが、式(12'-2), (12'-3)については 空間の離散化 で述べた通り離散化の方法が膨大にある。ここでは最も単純な1次精度風上差分法を採用しているが、単純ゆえにフクザツな現象には対応できないし誤差も溜まりやすい8。
これらを用いて式(12)を$q^{n}_{i, j}$について整理すれば下記のようになる。
q^{n+1}_{i, j} = q^{n}_{i, j} - \Delta t (c_{x} \frac{q^{n}_{i, j} - q^{n}_{i-1, j}}{\Delta x} + c_{z} \frac{q^{n}_{i, j} - q^{n}_{i, j-1}}{\Delta z}) \tag{15}
冒頭で貼り付けた 何が出来上がったのか の項も同様の離散化手法を採用しており、言ってしまえば計算精度も計算量も最低クラス。これ以降の事例では簡略化のため$\Delta x = \Delta y = 1$として式から除外している。
実装内容
さて、放物運動のときは時間差分だけを考えればよかったが今回は空間差分項も出てきてしまった。
「空間の離散化と隣接セルとの関係」を記述するため、gridノードにattribute wrangleノードをつないで下記のように記述する。
# [ global_param_q-1d ]
# gridの刻み幅 -> Size / Rows, Columns間にも適用
# CONTROLLER ( = Nullノードに変数を格納したもの ) から読み込み
float dx = ch("../CONTROLLER/dx");
float dz = ch("../CONTROLLER/dz");
# x, z方向の隣接点のpoint番号を取得しattributeに持つ
# i@x_for = nearpoint(0, @P+{dx,0,0}, 0); # 今回使わない
i@x_back = nearpoint(0, @P+{-dx,0,0}, 0);
# i@z_for = nearpoint(0, @P+{0,0,dz}, 0); # 今回使わない
i@z_back = nearpoint(0, @P+{0,0,-dz}, 0);
やたら冗長な記述なので何か良い代替案があればそれで置き換えたいのだが・・・
gridに於いて「前後左右のpoint番号」を取得する良い方法が浮かばなかったので、力技に近いが @P±dx,dz 周辺でnearpointを実行してattributeに格納することでそれを実現した。
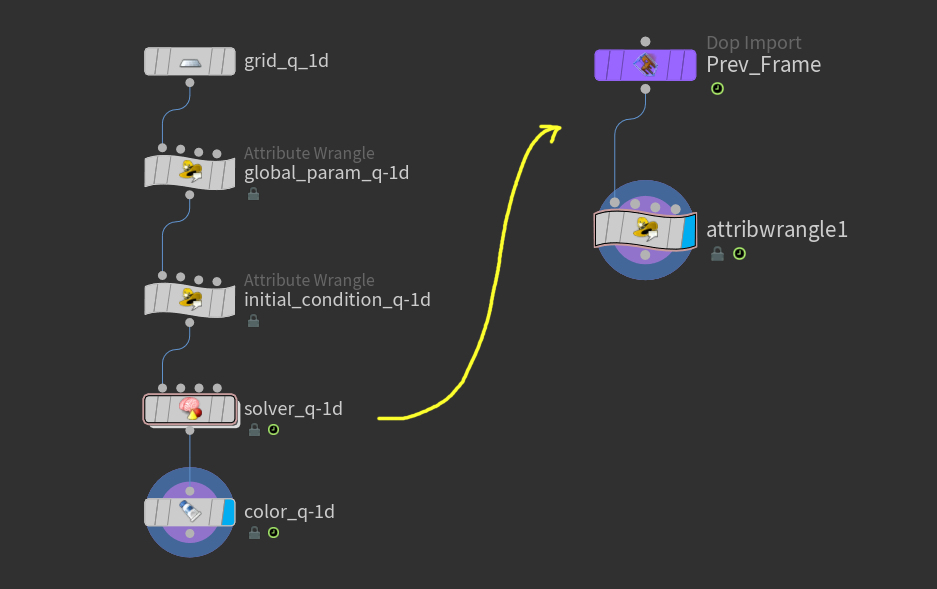
一応図式化するとこんな感じ。
移動させてみたい波は別にどんな形状でも良いのだが、VEXは陰関数形式で記述できない(正しい?)ためgrid中央付近だけ盛り上げる下記のような初期条件にしてみる。
# [ initial_condition_q-1d ]
# 取り敢えず中央付近の特定範囲だけ高さを持たせてみた
if (@P.x > -5 && @P.x < 5 && @P.z > -5 && @P.z < 5) {
@P.y = 5.0;
}
# 条件式が陰関数で定義できるなら単純な波面とかにしたかった
# if ( x + 2z > 5 ) {
# @P.y = 5.0;
# }
# みたいな。こっちのほうが波っぽい
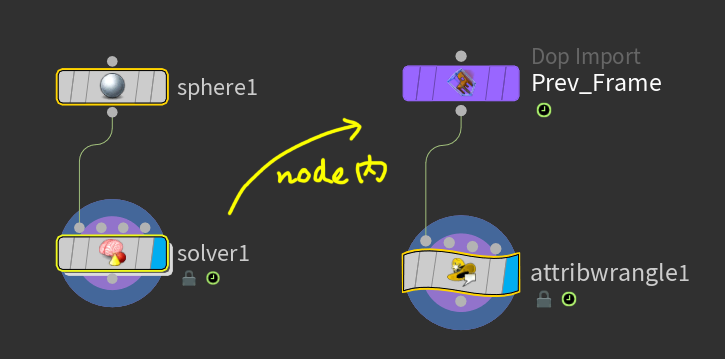
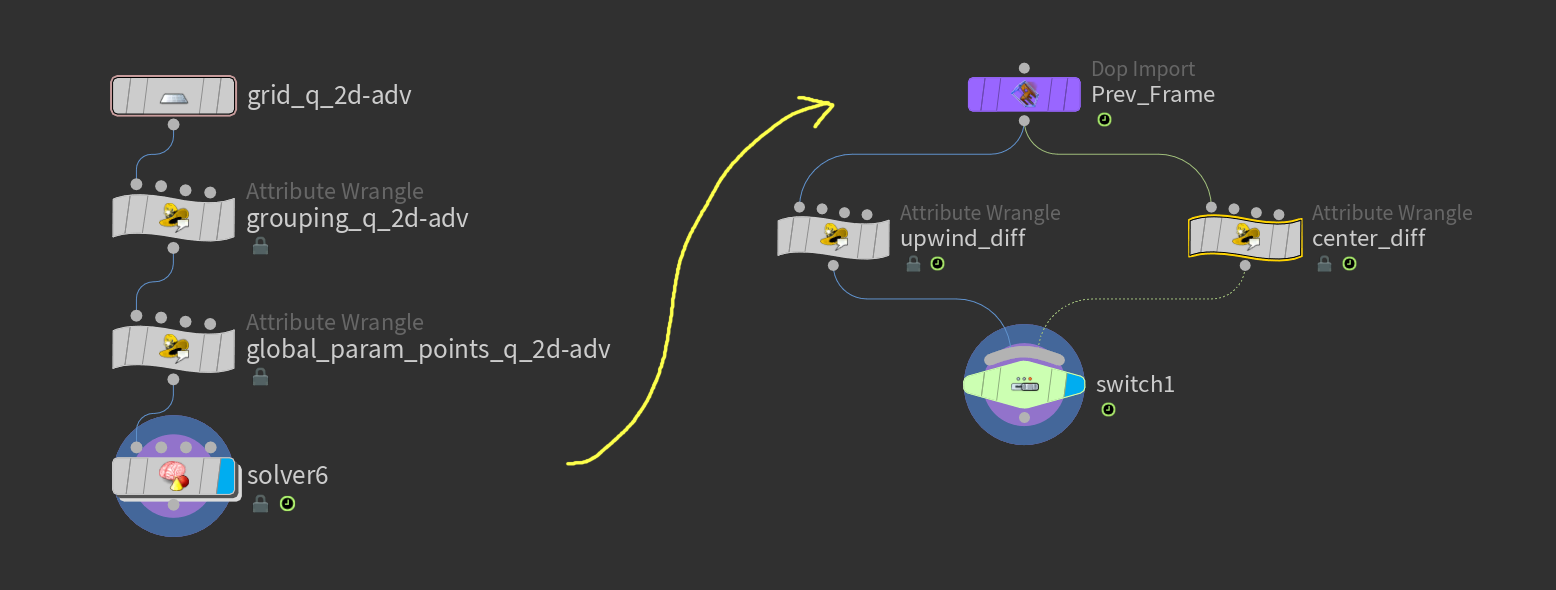
そして本題のsolver内部。
解説についてはコメントを参照のこと。
# [ attribwrangle_q-1d ]
# parameter読込
float c = ch("../../../../CONTROLLER/flow_speed"); # 波の進行速度
float dt = ch("../../../../CONTROLLER/dt"); # 時間幅
float theta = ch("../../../../CONTROLLER/theta"); # 波の進行角度
# old_u = u.copy() 的なもの
vector old_P = @P;
# j-1, i-1に当たるpoint番号を取得する
int index_xback = point(0, "x_back", @ptnum);
int index_zback = point(0, "z_back", @ptnum);
# gridの境界=端っこは計算対象から除外(いずれここはgroupingで解決することになる)
if ( abs(@P.x) != ch("../../../../grid_q-1d/sizex")/2 ||
abs(@P.z) != ch("../../../../grid_q-1d/sizez")/2 ) {
# 移流方程式を計算する
# xback, zbackが存在しない場合を除外する
if ( index_xback>0 || index_zback>0 ){
# q_(i, j-1), q_(i-1, j)に当たる点の座標を取得する
vector p_xback = point(0, "P", index_xback);
vector p_zback = point(0, "P", index_zback);
# 更新したいのはy座標なのでy成分で加減算
# cx = c*sin(theta), cz = c*cos(theta) と展開している
@P.y += -dt * ((@P.y - p_xback.y) * c * sin(theta) + (@P.y - p_zback.y) * c * cos(theta));
}
}
# colorで可視化する用にattributeを定義してみる
f@height = @P.y;
実行結果
仮にこんな感じの部分的に盛り上がった波が特定の速度、角度で進んでいったらこうなるでしょう、というやつ。

qがベクトル(2次元)量の場合
この辺りから流れのシミュレーションに直結する応用編。
といいつつやることは1次元の場合とほとんど変わらないので機械的に並べていく。
方程式
平面の流れをx軸方向の速度u、z軸方向の速度vの2次元量で表す。つまり
(u, v) → (u(t, \boldsymbol{r}(x, z), v(t, \boldsymbol{r}(x, z)) → (u^{n}_{i, j}, v^{n}_{i, j}) \tag{16}
式(15)の形に寄せると
\begin{eqnarray}
\begin{bmatrix}
\displaystyle u^{n+1}_{i, j} \\
\\
\displaystyle v^{n+1}_{i, j} \\
\end{bmatrix}
=
\begin{bmatrix}
u^{n}_{i, j} - \Delta t \displaystyle (c_{x} \frac{u^{n}_{i, j} - u^{n}_{i-1, j}}{\Delta x} + c_{z} \frac{u^{n}_{i, j} - u^{n}_{i, j-1}}{\Delta z}) \\
\\
v^{n}_{i, j} - \Delta t \displaystyle (c_{x} \frac{v^{n}_{i, j} - v^{n}_{i-1, j}}{\Delta x} + c_{z} \frac{v^{n}_{i, j} - v^{n}_{i, j-1}}{\Delta z}) \\
\end{bmatrix} \tag{17}
\end{eqnarray}
実装内容
単にq=@P.yからq=(u, v)に増えただけなのだが、段々混沌としてきた。
(実際この辺りは自分でも混乱して1,2週間頭から離れなくなった)
1次精度なので高が知れているが、一応2パターンで計算してみる。
# [ grouping_q_2d-adv ]
# -x軸方向, z軸方向の端を"flow" groupとする
# その逆端を"boundary" groupとする
if ( @P.x == -ch("../grid_q_2d-adv/sizex")/2 ||
@P.z == ch("../grid_q_2d-adv/sizex")/2 ) {
setpointgroup(geoself(), "flow", @ptnum, 1, "set");
} else if ( @P.x == ch("../grid_q_2d-adv/sizex")/2 ||
@P.z == -ch("../grid_q_2d-adv/sizex")/2) {
setpointgroup(geoself(), "boundary", @ptnum, 1, "set");
}
# [ global_param_points_q_2d-adv ]
# 刻み幅読み込み
float dx = ch("../CONTROLLER/dx_q_2d-adv");
float dz = ch("../CONTROLLER/dy_q_2d-adv");
# 流入条件 + 一定流条件
if (@group_flow == 1) {
f@vel_u = 6.0;
f@vel_v = 3.0;
} else {
f@vel_u = 1.0;
f@vel_v = 2.0;
}
# 可視化のための「速度」の定義
# 上から見下ろしたときの平面方向のみの速度なので第2成分は0
v@vel = set(@vel_u, 0, @vel_v);
# いつものやつ
i@x_for = nearpoint(0, @P+set(dx,0,0), 0);
i@x_back = nearpoint(0, @P+set(-dx,0,0), 0);
i@z_for = nearpoint(0, @P+set(0,0,dz), 0);
i@z_back = nearpoint(0, @P+set(0,0,-dz), 0);
これってどういう状況かというと、一様に$(u, v)=(1.0, 2.0)$の速度で風が流れているなか、両角を流れる$(u, v)=(6.0, 3.0)$の風が流れ込んできたとき。のシミュレーション。角部屋で窓を開けたときとかだろうか。
幾つか可視化の手法は試したが、処理速度との兼ね合いでVisualization > Markerで@velattributeを表示することにした。見え方については実行結果の項を参照。
# [ upwind_diff ]
# CONTROLLERノードから変数を読み取る
float dt = ch("../../../../CONTROLLER/dt_q_2d-adv");
float dx = ch("../../../../CONTROLLER/dx_q_2d-adv");
float dy = ch("../../../../CONTROLLER/dy_q_2d-adv");
# 計算前に一旦前ステップの値を格納(Solverノードの仕様上、これに意味があるかどうかよく解ってない)
f@old_u = @vel_u;
f@old_v = @vel_v;
v@old_vel = @vel;
# アトリビュートに格納しておいた前後左右の点のindexを取り出し
int index_xback = point(0, "x_back", @ptnum);
int index_xfor = point(0, "x_for", @ptnum);
int index_zback = point(0, "z_back", @ptnum);
int index_zfor = point(0, "z_for", @ptnum);
# その各点における(u, v)の値を呼び出す
float u_xback = point(0, "old_u", index_xback);
float u_xfor = point(0, "old_u", index_xfor);
float u_zback = point(0, "old_u", index_zback);
float u_zfor = point(0, "old_u", index_zfor);
float v_xback = point(0, "old_v", index_xback);
float v_xfor = point(0, "old_v", index_xfor);
float v_zback = point(0, "old_v", index_zback);
float v_zfor = point(0, "old_v", index_zfor);
# gridの端を除く中の各点のu, vに対して1次風上差分法を実行
if ( @group_flow != 1 && @group_boundary != 1 ) {
if ( @old_u >= 0 && @old_v >= 0 ) {
@vel_u += -dt * ( @old_u * ( @old_u - u_xback ) + @old_v * ( @old_u - u_zback ) );
@vel_v += -dt * ( @old_u * ( @old_v - v_xback ) + @old_v * ( @old_v - v_zback ) );
} else if ( @old_u < 0 && @old_v >= 0 ) {
@vel_u += -dt * ( @old_u * ( u_xfor - @old_u ) + @old_v * ( @old_u - u_zback ) );
@vel_v += -dt * ( @old_u * ( v_xfor - @old_v ) + @old_v * ( @old_v - v_zback ) );
} else if ( @old_u >= 0 && @old_v < 0 ) {
@vel_u += -dt * ( @old_u * ( @old_u - u_xback ) + @old_v * ( u_zfor - @old_u ) );
@vel_v += -dt * ( @old_u * ( @old_v - v_xback ) + @old_v * ( v_zfor - @old_v ) );
} else {
@vel_u += -dt * ( @old_u * ( u_xfor - @old_u ) + @old_v * ( u_zfor - @old_u ) );
@vel_v += -dt * ( @old_u * ( v_xfor - @old_v ) + @old_v * ( v_zfor - @old_v ) );
}
} else if( @group_boundary == 1 ) {
@vel_u = 1.0;
@vel_v = 2.0;
} else {
@vel_u = 4.0;
@vel_v = 3.0;
}
@vel = set(@vel_u, 0, @vel_v);
上記の風上差分項を中心差分項で置き換えたものはこちら。
# [ center_diff ]
# gridの端を除く中の各点のu, vに対して中心風上差分法を実行
if ( @group_flow != 1 && @group_boundary != 1 ) {
@vel_u += -dt * ( @old_u * ( 2 * @old_u - u_xfor - u_xback ) + @old_v * ( 2 * @old_u - u_zfor - u_zback ) );
@vel_v += -dt * ( @old_u * ( 2 * @old_v - v_xfor - v_xback ) + @old_v * ( 2 * @old_v - v_zfor - v_zback ) );
} else if( @group_boundary == 1 ) {
@vel_u = 1.0;
@vel_v = 2.0;
} else {
@vel_u = 6.0;
@vel_v = 3.0;
}
@vel = set(@vel_u, 0, @vel_v);
実行結果
風上差分はこっち。
風上(=風が吹いてくる方向)の情報のみを取得しているため、右奥の流速(赤矢印)は結果に寄与しない。
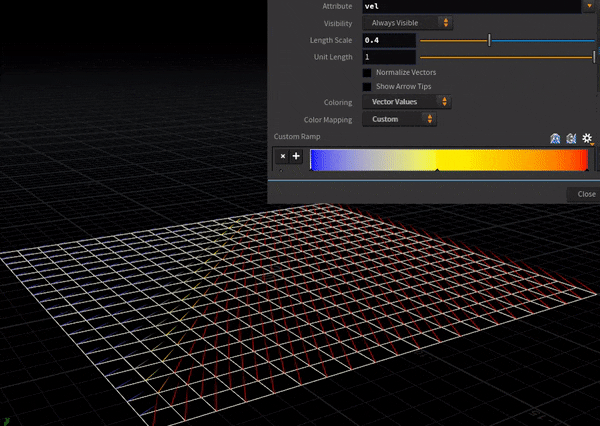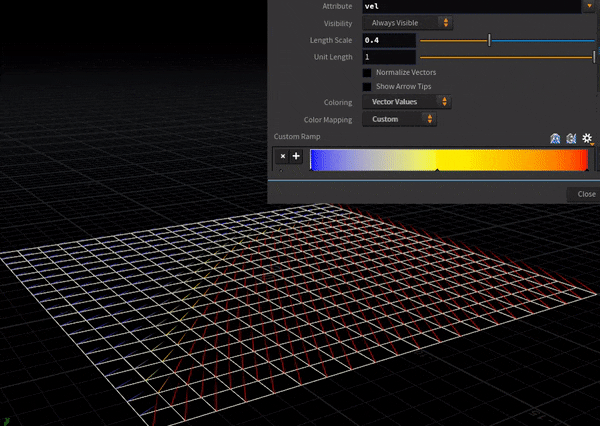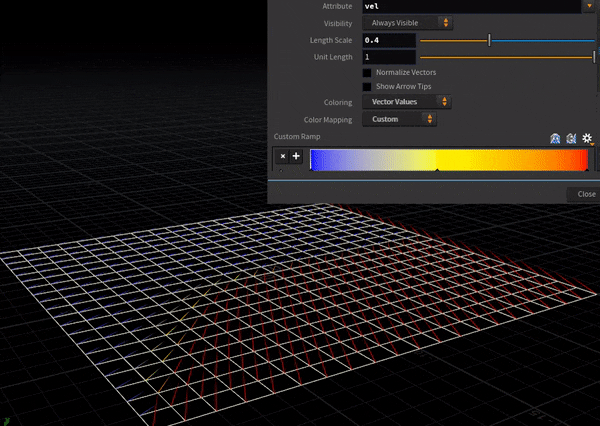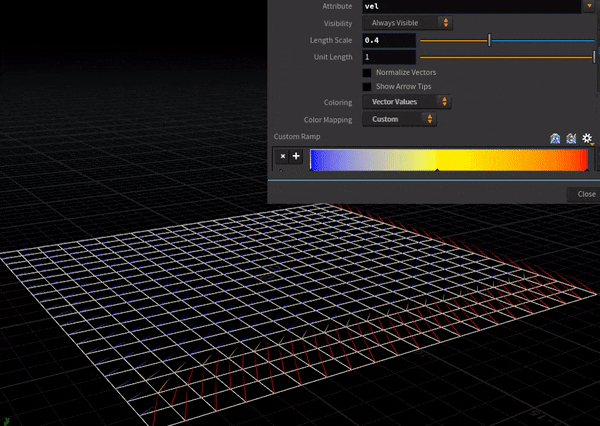
中央差分はこっち。各点においてその周辺4点の情報を取得するため、両端からじわじわと流速が上がっていく様子が確認できる。
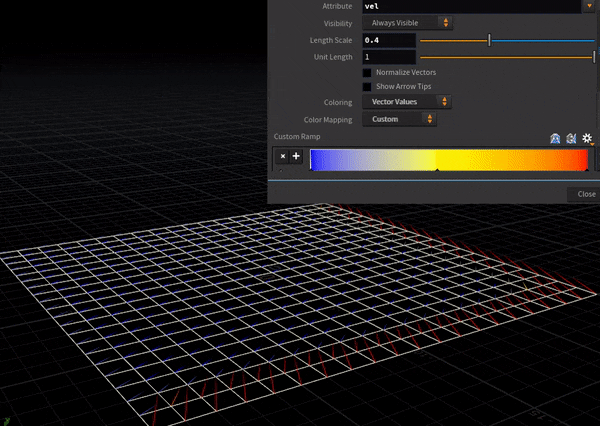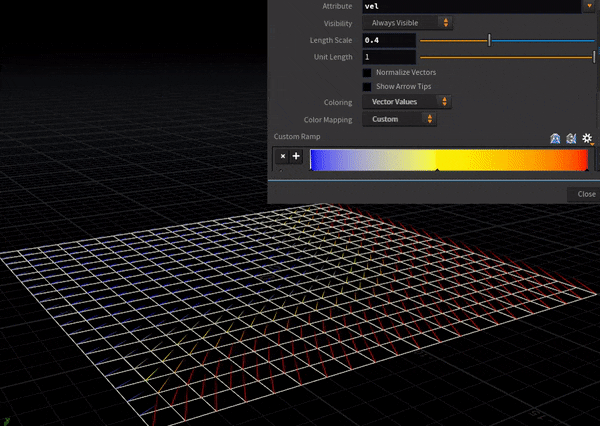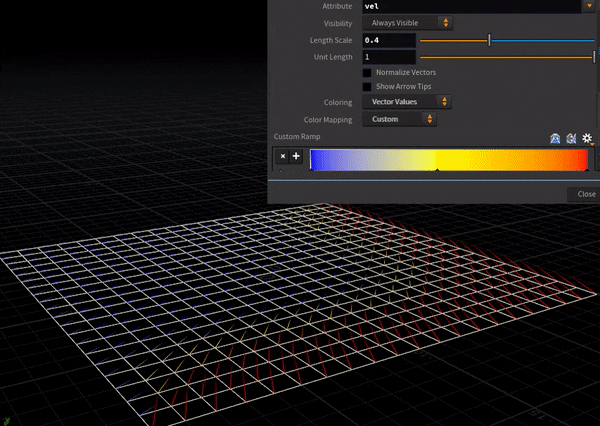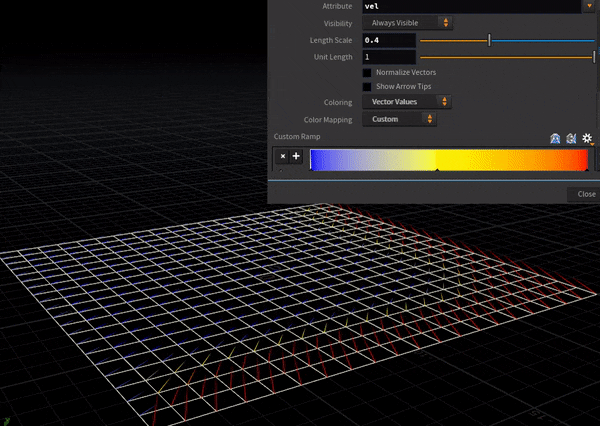
こんな単純な2例でも「現象をとらえた計算モデルを採用する」ことの重要さの片鱗が見える。
拡散方程式
もうすでに文字数が多すぎるのと、ほとんど移流方程式とやることが変わらないので方程式、Solverノード内attribute wrangle、実行結果だけ機械的に並べていくことにする。
qがスカラー量の場合
水中にインクを垂らしたときの広がり、とか熱の広がり、とか割といろんな現象がこの形式だった気がする。
拡散方程式に関しては逆に1次元の場合のほうがイメージしやすいかもしれない。
\frac{\partial q}{\partial t} - D\frac{\partial^2 q}{\partial \boldsymbol{r}^2} = \frac{\partial q}{\partial t} - D ( \frac{\partial^2 q}{\partial x^2} + \frac{\partial^2 q}{\partial z^2}) = 0 \tag{13'}
これを整理して
q^{n+1}_{i, j} = q^{n}_{i, j} + D (\displaystyle \frac{ q^{n}_{i-1, j} + q^{n}_{i+1, j} - 2q^{n}_{i, j} }{(\Delta x)^2} + \displaystyle \frac{ q^{n}_{i, j-1} + q^{n}_{i, j+1} - 2q^{n}_{i, j} }{(\Delta z)^2})\Delta t \tag{18}
そしてSolver内attribute wrangleはこう。
# 例によってparameter読み込み
float dt = ch("../../../../CONTROLLER/dt_q_1d-diff");
float dx = ch("../../../../CONTROLLER/dx_q_1d-diff");
float dy = ch("../../../../CONTROLLER/dy_q_1d-diff");
# 拡散係数D
float dif = ch("../../../../CONTROLLER/diff_coef");
# 前ステップの値格納
vector old_P = @P;
# いつもの
int index_xback = point(0, "x_back", @ptnum);
# ---以下略---
# 境界条件
if ( abs(@P.x) == ch("../../../../grid_q_1d-diff/sizex")/2 ||
( abs(@P.z) == ch("../../../../grid_q_1d-diff/sizey")/2 ) ) {
@P.y = 0;
} else {
# 違いはここだけ
@P.y += dif * dt * ( (p_xback.y + p_xfor.y - 2*old_P.y) + (p_zback.y + p_zfor.y - 2*old_P.y) );
}
# 可視化用
f@height = @P.y;
実行結果はこう。
(初期条件の置き方が悪いのだが)見栄え的にあんまり移流方程式と変わらない。。
qがベクトル(2次元)量の場合
こちらも移流方程式を1→2次元にしたときと同様。
\begin{eqnarray}
\begin{bmatrix}
\displaystyle u^{n+1}_{i, j} \\
\\
\displaystyle v^{n+1}_{i, j} \\
\end{bmatrix}
=
\begin{bmatrix}
u^{n}_{i, j} + D (\displaystyle \frac{ u^{n}_{i-1, j} + u^{n}_{i+1, j} - 2u^{n}_{i, j} }{(\Delta x)^2} + \displaystyle \frac{ u^{n}_{i, j-1} + u^{n}_{i, j+1} - 2u^{n}_{i, j} }{(\Delta z)^2})\Delta t \\
\\
v^{n}_{i, j} + D (\displaystyle \frac{ v^{n}_{i-1, j} + v^{n}_{i+1, j} - 2v^{n}_{i, j} }{(\Delta x)^2} + \displaystyle \frac{ v^{n}_{i, j-1} + v^{n}_{i, j+1} - 2v^{n}_{i, j} }{(\Delta z)^2})\Delta t \\
\end{bmatrix} \tag{17}
\end{eqnarray}
初期条件はこんな感じにしてみた。
# 一様流れの中で一部だけ流速が上がった場合(扇風機とかエアコンとかか)
if (@group_flow_point == 1) {
f@vel_u = 10.0;
f@vel_v = 5.0;
} else {
f@vel_u = 2.0;
f@vel_v = 2.0;
}
grid端以外の式がちょっと変わる。
# いつもの
float dt = ch("../../../../CONTROLLER/dt_q_2d-diff");
float dx = ch("../../../../CONTROLLER/dx_q_2d-diff");
float dy = ch("../../../../CONTROLLER/dy_q_2d-diff");
# 拡散係数D
float vis = ch("../../../../CONTROLLER/diff_coef");
# 前ステップの結果格納
f@old_u = @vel_u;
f@old_v = @vel_v;
# いつもの
int index_xback = point(0, "x_back", @ptnum);
# ---以下略---
# 境界条件は固定値
if( @group_boundary == 1 ) {
@vel_u = 2.0;
@vel_v = 2.0;
} else {
# 違いはここだけ
@vel_u += vis * dt * ( (u_xback + u_xfor- 2*@old_u) + (u_zback + u_zfor - 2*@old_u) );
@vel_v += vis * dt * ( (v_xback + v_xfor- 2*@old_v) + (v_zback + v_zfor - 2*@old_v) );
}
流速を供給し続けない限りはのっぺり広がっちゃうよ、の図。
冒頭のGIFはこれらの「流れの移動」+「流れの拡散」の2つの現象だけ盛り込んだビル周りのシミュレーション、ということになる。
展望編:今後の着手箇所
ここにたどり着くまでに何度か言及したが、圧力項を加えなければ最低限流れのシミュレーションとは呼べない。
そこまで実装したうえで緯度・経度を変えながら計算してやっとHoudiniである意味が出るという。
しかし圧力項の計算を説明するにはまずLaplace方程式、次にPoission方程式とステップを踏みたい。
そうするとgrid数サイズの行列計算も出てくる(しかも対角以外も成分を持つ)し収束条件も加味しなければいけない、それってVEXでできる計算量なのかpythonライブラリの力を借りたほうがいいのか、もはやVEXでやる必要はあるのか、・・・みたいな話になってきそうなのでこの辺で区切ることにした次第。
とりあえず書き上げてみて思ったことは2つ。
1つ目。正直講義を受けていた当時は全然理解できなかったし記事書き始め時点で知識0みたいなもんだったので、テーマを決めてから書籍を5冊くらい購入してしまった。一発ネタの予定だったけどほんの少しだけこの分野に詳しくなれたので、今後もちまちま進めてみてまた形になったころに記事にしてみようかと。
2つ目。
やっぱり本家は凄い。たったこれだけの実装で既に動作モッサリになるとは思わなかった。。
大人しくPyroを使おう。
以上。
その他参考文献はまとめてここ9 10 11 12 13に挙げておく。