【自己組織化マップ】多次元情報を可視化する

初めに

前回の記事では、画像データを例に自己組織化マップ(以下、SOM)の説明を記事にした
今回は、California HousingのデータでSOMを活用した
データの解釈の方法について記事にしようと思う。

私自身、SOMから得られた解釈をプレゼンするは非常に苦労するし、
なかなか分かってもらえないものだ・・・
ただし、自分のデータ分析にのみ活用する際、SOMは有効な手段だと考えている。

データの前処理

これについては、過去の記事と同様の処理を実施する
コードについては、下記の通り

# ライブラリのインポート
import pandas as pd
import numpy as np
import seaborn as sns
import time
from sklearn.datasets import fetch_california_housing

#california housingデータのインポート
cali_housing = fetch_california_housing(as_frame=True)
x=cali_housing.data
y=cali_housing.target
df=cali_housing.frame

#標準偏差による外れ値処理
ar_std=df['AveRooms'].std()
ab_std=df['AveBedrms'].std()
pop_std=df['Population'].std()
ao_std=df['AveOccup'].std()
mhv_std=df['MedHouseVal'].std()

ar_mean=df['AveRooms'].mean()
ab_mean=df['AveBedrms'].mean()
pop_mean=df['Population'].mean()
ao_mean=df['AveOccup'].mean()
mhv_mean=df['MedHouseVal'].mean()

limit_low=ar_mean - 1*ab_std
limit_high=ar_mean + 1*ab_std

limit_low1=ab_mean - 1*ab_std
limit_high1=ab_mean + 1*ab_std

limit_low2=pop_mean - 1*pop_std
limit_high2=pop_mean + 1*pop_std

limit_low3=ao_mean - 0.5*ao_std
limit_high3=ao_mean + 0.5*ao_std

limit_low4=mhv_mean -1*mhv_std
limit_high4=mhv_mean +1*mhv_std
newdf=df.query('@limit_low < AveRooms < @limit_high')
newdf1=newdf.query('@limit_low1 < AveBedrms < @limit_high1')
newdf2=newdf1.query('@limit_low2 < Population < @limit_high2')
newdf3=newdf2.query('@limit_low3 < AveOccup < @limit_high3')
newdf4=newdf3.query('@limit_low4 < MedHouseVal < @limit_high4')

#外れ値処理後、正規化する
#正規化(Max-Min法)
def minmax_norm(df):
    return (df - df.min()) / ( df.max() - df.min())

df_minmax_norm = minmax_norm(newdf4)
df_minmax_norm

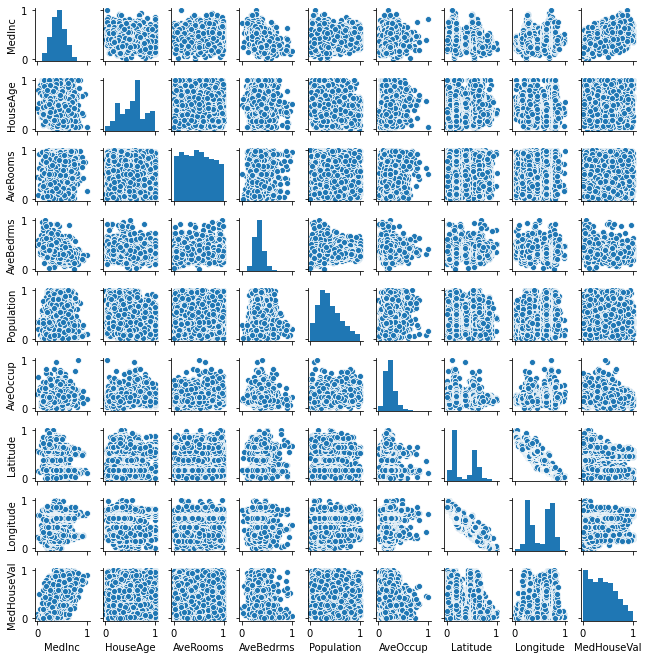
# 多変量連関図
sns.pairplot(df_minmax_norm, size=1.0)

SOMの初期場を構築する

本検討では10行・50列のSOMで構築する。
California housingのデータセットの因子数は9つであるので、
SOM1つのユニットの次元数は9である。

#SOMの行・列を定義する
scol=50#列
srow=10#行

#somのサイズ・ベクトルを定義しておく
#今回のデータは因子数9つなので9次元分確保しておく
som = np.random.random_sample(size=(srow, scol, 9)) # map construction


#各次元用の可視化SOM（9次元分を可視化するための設定）
som1 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som2 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som3 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som4 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som5 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som6 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som7 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som8 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som9 = np.random.random_sample(size=(srow, scol, 3)) # map construction

#端末依存性によらない乱数発生シードを定義する
np.random.seed(0)

#初期場を作る
ii=0
jj=0
for ii in range(srow):
    for jj in range(scol):
        #np.random.randomは0.0以上1.0未満の範囲で連続一様分布で乱数発生する
        som[ii][jj]= np.random.random(9)#()内の3は3つだけ乱数を発生する意味
        som1[ii][jj]=(som[ii,jj,0],1,1)
        som2[ii][jj]=(som[ii,jj,1],1,1)
        som3[ii][jj]=(som[ii,jj,2],1,1)
        som4[ii][jj]=(som[ii,jj,3],1,1)
        som5[ii][jj]=(som[ii,jj,4],1,1)
        som6[ii][jj]=(som[ii,jj,5],1,1)
        som7[ii][jj]=(som[ii,jj,6],1,1)
        som8[ii][jj]=(som[ii,jj,7],1,1)
        som9[ii][jj]=(som[ii,jj,8],1,1)

SOMの設定

学習回数、近傍ユニット数、学習率の設定を行う。
学習回数：10回
近傍ユニット数：2
学習率：0.3
で近傍関数、重みの更新は前回の記事と同じ設定である。

#学習回数
T=10
#近傍ユニット数
unit=5
#学習率0<a<1
a=0.3
#datasetの行数を取得する
count=len(df_minmax_norm)
print(count)
#ユークリッド距離・マンハッタン距離用のサイズを定義しておく
e_dis = np.random.random_sample(size=(count,1)) # map construction
m_dis = np.random.random_sample(size=(srow,scol,1)) # map construction

#カウンターなどの初期化
min_e_dis=1
min_ii=0
min_jj=0
min_si=0
min_sj=0

SOMを実行する

for step in range(T):
    ct=0
    si=0
    sj=0
    min_ct=0
    min_si=0
    min_sj=0
    # 処理前の時刻
    t1 = time.time() 
    for ct in range(count):
        #入力データに類似する勝利ユニットを探索する####################################
        min_e_dis=1
        for si in range(srow):
            for sj in range(scol):
                aa=df_minmax_norm.iloc[ct,0]
                bb=df_minmax_norm.iloc[ct,1]
                cc=df_minmax_norm.iloc[ct,2]
                dd=df_minmax_norm.iloc[ct,3]
                ee=df_minmax_norm.iloc[ct,4]
                ff=df_minmax_norm.iloc[ct,5]
                gg=df_minmax_norm.iloc[ct,6]
                hh=df_minmax_norm.iloc[ct,7]
                ii=df_minmax_norm.iloc[ct,8]
                soa=som[si,sj,0]
                sob=som[si,sj,1]
                soc=som[si,sj,2]
                sod=som[si,sj,3]
                soe=som[si,sj,4]
                sof=som[si,sj,5]
                sog=som[si,sj,6]
                soh=som[si,sj,7]
                soi=som[si,sj,8]
                e_dis[ct,0]=np.sqrt( (aa-soa)**2 + (bb-sob)**2 + (cc-soc)**2+
                                      (dd-sod)**2 + (ee-soe)**2 + (ff-sof)**2+
                                      (gg-sog)**2 + (hh-soh)**2 + (ii-soi)**2)
                #print(e_dis[ct,0])
                if(e_dis[ct,0]<min_e_dis) :
                    min_e_dis=e_dis[ct,0]
                    min_ct=ct
                    min_si=si
                    min_sj=sj
            #########################################################################################
            sii=0
            sjj=0
            for sii in range(srow):
                for sjj in range(scol):
                    #マンハッタン距離
                    m_dis[sii][sjj]=abs(sii-min_si)+abs(sjj-min_sj)
                    allowrange=(1-(step/T))*unit
                    #print(si,sj,unitdis[si,sj,0])
                    if(m_dis[sii,sjj,0]<=allowrange):
                        #print(sii,sjj,unitdis[si,sj,0])
                        #print("update",sii,sjj)
                        som[sii,sjj,0]+=(df_minmax_norm.iloc[min_ct,0]-som[sii,sjj,0])*a*(1-((step+1)/T))
                        som[sii,sjj,1]+=(df_minmax_norm.iloc[min_ct,1]-som[sii,sjj,1])*a*(1-((step+1)/T))
                        som[sii,sjj,2]+=(df_minmax_norm.iloc[min_ct,2]-som[sii,sjj,2])*a*(1-((step+1)/T))
                        som[sii,sjj,3]+=(df_minmax_norm.iloc[min_ct,3]-som[sii,sjj,3])*a*(1-((step+1)/T))
                        som[sii,sjj,4]+=(df_minmax_norm.iloc[min_ct,4]-som[sii,sjj,4])*a*(1-((step+1)/T))
                        som[sii,sjj,5]+=(df_minmax_norm.iloc[min_ct,5]-som[sii,sjj,5])*a*(1-((step+1)/T))
                        som[sii,sjj,6]+=(df_minmax_norm.iloc[min_ct,6]-som[sii,sjj,6])*a*(1-((step+1)/T))
                        som[sii,sjj,7]+=(df_minmax_norm.iloc[min_ct,7]-som[sii,sjj,7])*a*(1-((step+1)/T))
                        som[sii,sjj,8]+=(df_minmax_norm.iloc[min_ct,8]-som[sii,sjj,8])*a*(1-((step+1)/T))

            #########################################################################################
    # 処理後の時刻
    t2 = time.time()
    # 経過時間を表示
    elapsed_time = t2-t1
    print(f"経過時間：{elapsed_time}")
    print("step",step)

可視化する

#各次元用の可視化SOM
som1 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som2 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som3 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som4 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som5 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som6 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som7 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som8 = np.random.random_sample(size=(srow, scol, 3)) # map construction
som9 = np.random.random_sample(size=(srow, scol, 3)) # map construction
ii=0
jj=0
for ii in range(srow):
    for jj in range(scol):
        som1[ii][jj]=(som[ii,jj,0],1,1)
        som2[ii][jj]=(som[ii,jj,1],1,1)
        som3[ii][jj]=(som[ii,jj,2],1,1)
        som4[ii][jj]=(som[ii,jj,3],1,1)
        som5[ii][jj]=(som[ii,jj,4],1,1)
        som6[ii][jj]=(som[ii,jj,5],1,1)
        som7[ii][jj]=(som[ii,jj,6],1,1)
        som8[ii][jj]=(som[ii,jj,7],1,1)
        som9[ii][jj]=(som[ii,jj,8],1,1)

ちなみに、1次元目を可視化する際は下記のように実行する。

#1次ベクトルの可視化
plt.imshow(som1)

多次元情報の解析

上記のように1次から9次ベクトルまで可視化することで多次元情報を理解することができる。
今回は下図のようにまとめた。
本検討ではSOMの色味が白いほど因子の数値が高いと解釈する。
結果の解釈では
　①低緯度で高価な住宅価格であるグループは築年数が古く、部屋数が多い
　②高緯度で高価な住宅価格であるグループは築年数が古く、部屋数が多い
　③所得、ベッドルームの数、世帯数はほとんど住宅価格に影響がない
と理解できた。

注意点
特徴を捉える時は、各マップの同座標に情報の繋がりがあるので、
同座標の色の濃淡からどんな特徴があるか解釈する

最後に

上記のように、9次元データをSOM実行し、その後、各因子(各ベクトル)毎に可視化することで特徴把握が楽にできるようになります。
まぁ、どんな手法でも言えるが、統計的な分析だけを鵜吞みにするのではなく
なぜこの因子と特性値は相関があるのか？と考えながら解釈することが重要だと考えます。
最後までお読みいただきありがとうございました。