【自己組織化マップ】類は友を呼ぶ

初めに

自己組織化マップのイメージは、まさに類は友を呼ぶということわざのイメージがしてならない
(出典：デジタル大辞泉（小学館）)

2009年に私がこの手法に出会い、多次元情報を可視化できる点で感動した記憶がある
今回は今一度、理解を深めるために自己組織化マップについて記事にしようと思う

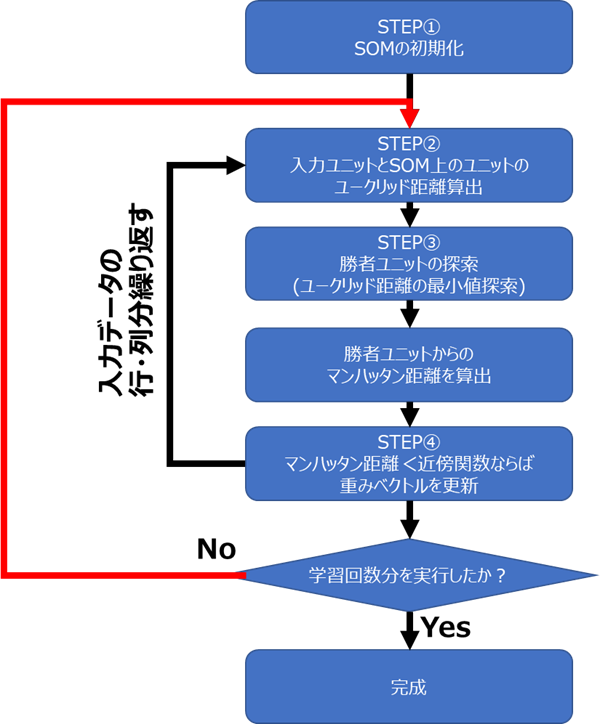
フロー図

自己組織化マップの簡単なフロー図は下図の通り

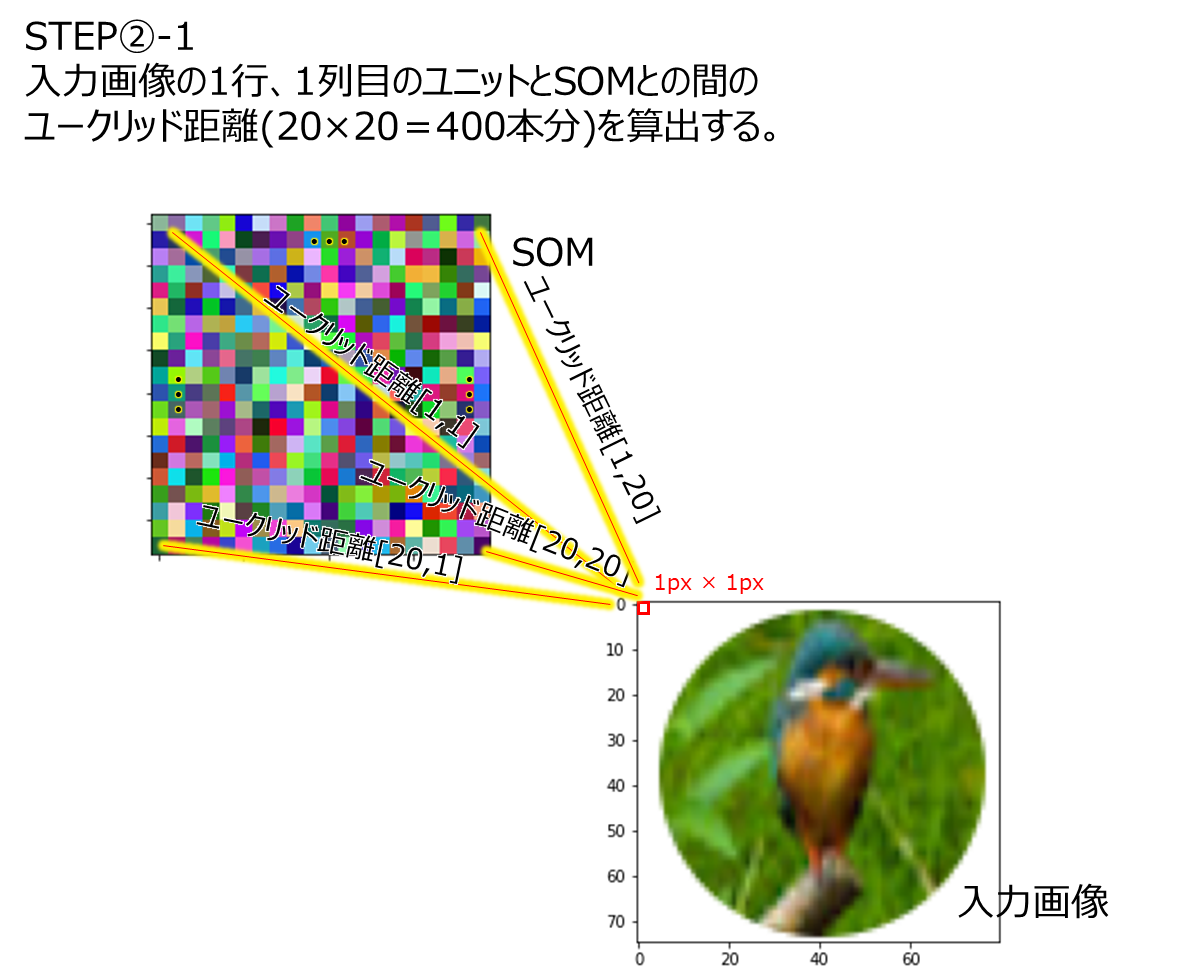
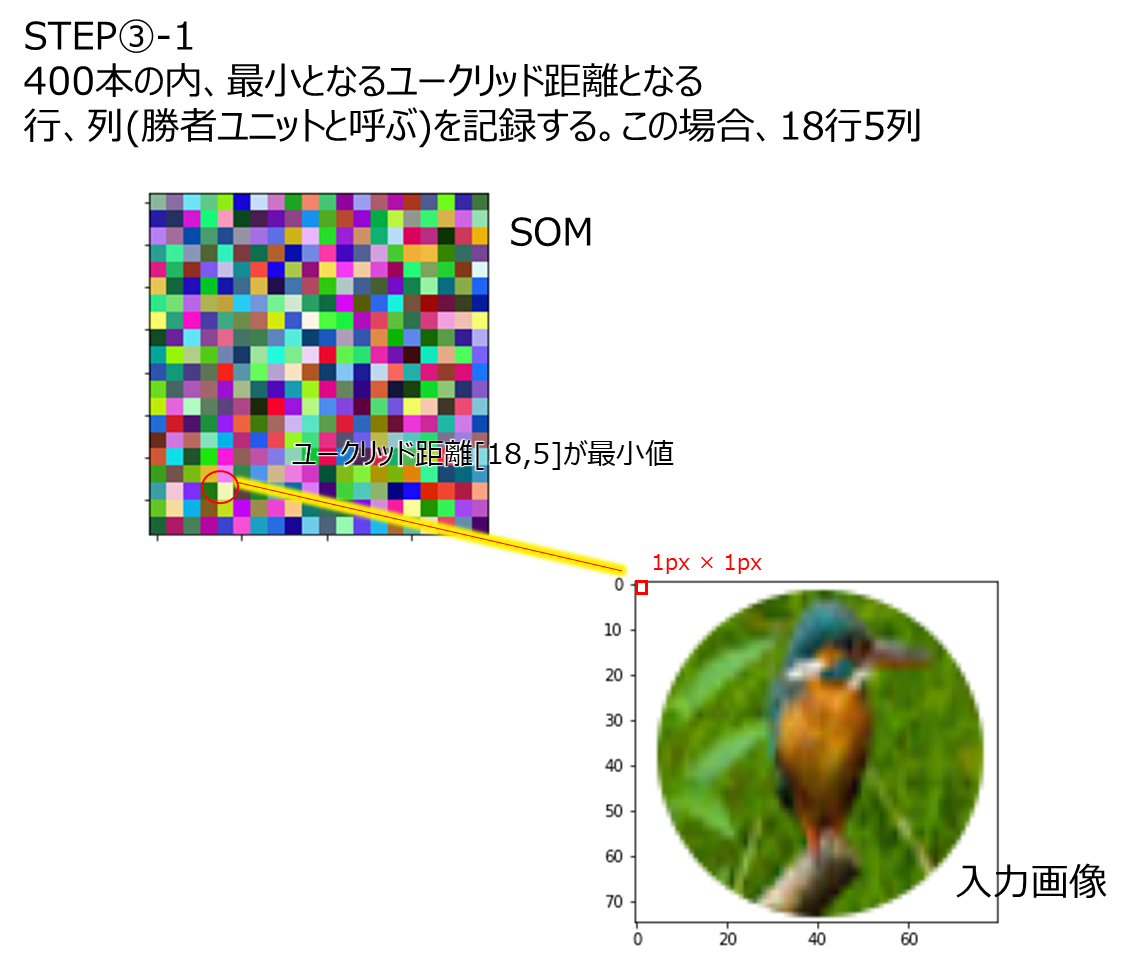
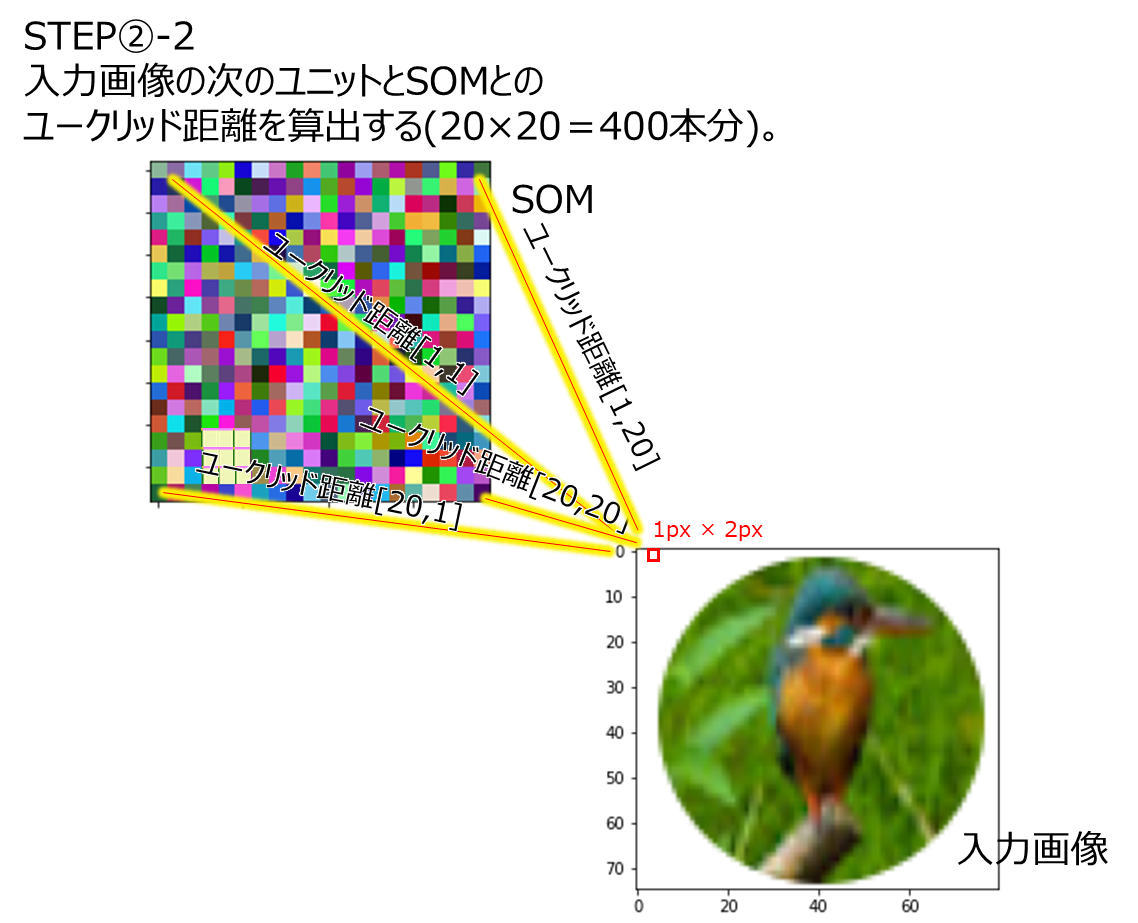
イメージ図

フロー図では分かり難いと思うので、イメージ図を描いてみる。

御覧いただいたように自己組織化マップはループ回数が膨大となる点注意が必要である。
特にSOMが大きくなるほど、計算回数は膨大となるため注意が必要である。

サンプル問題設定

今回はSOM（20×20ユニット）
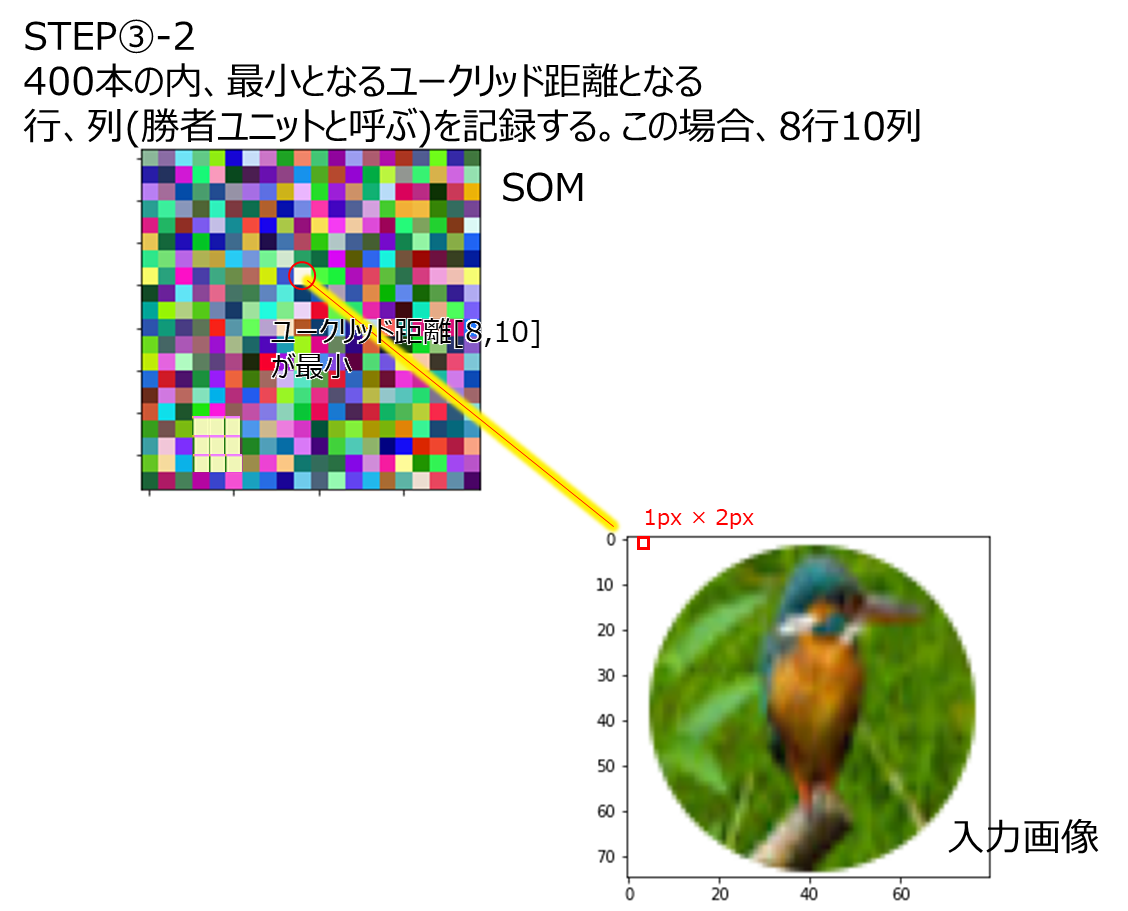
入力データは下図のkingfisher.png(75×80 px)とする。

・学習回数T 10回
・学習率α 0.3（ちなみに　0<α<1　）
・近傍ユニット数 2
・近傍関数は下記の通り

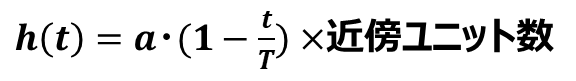
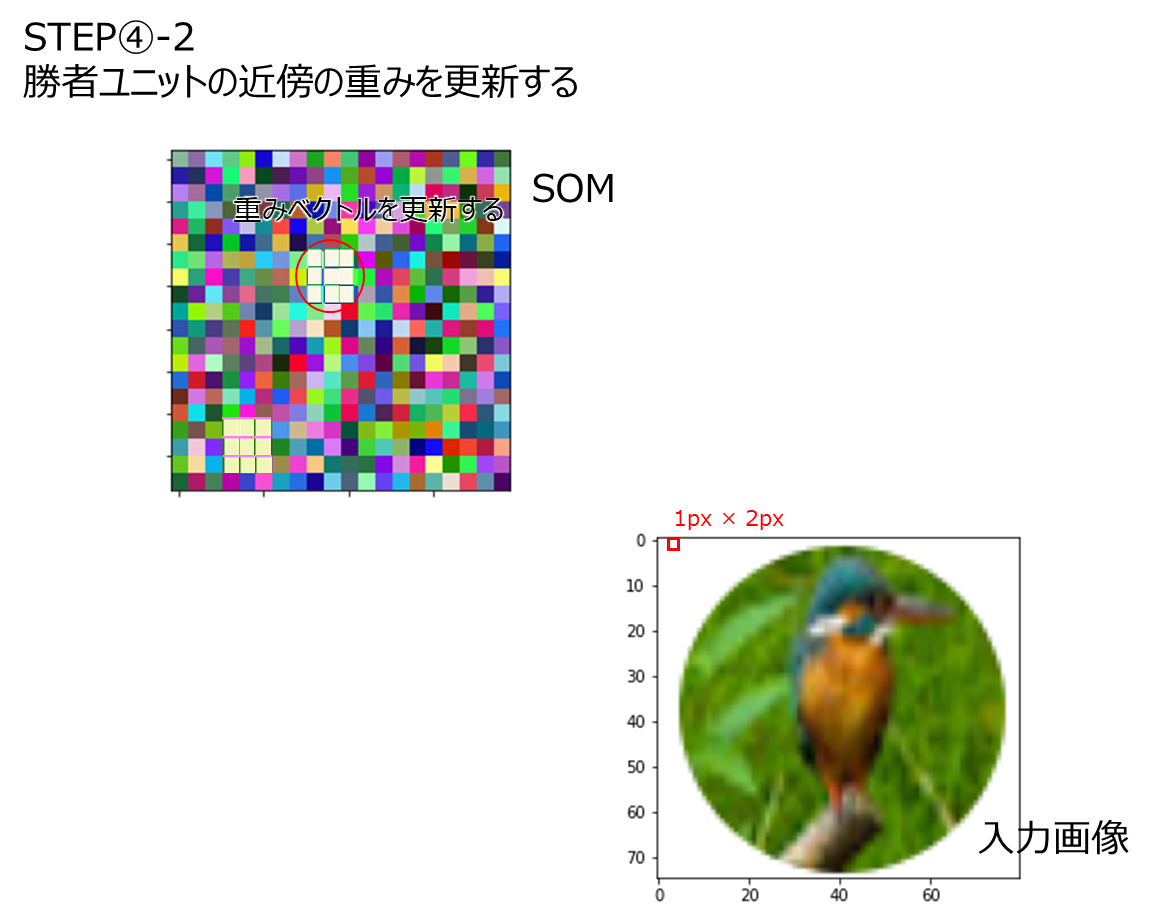
・重みベクトルの更新は下記の通り

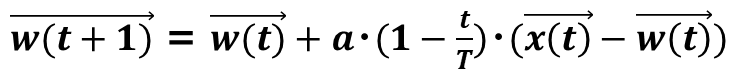
それではコードを下記に書く。

ライブラリをインポート

import numpy as np
from numpy.ma.core import ceil
import matplotlib.pyplot as plt
from matplotlib import animation, colors

SOMの初期場を構築する

#SOMの行・列を定義する
scol=20#列
srow=20#行

#somのサイズ・ベクトルを定義しておく
#今回は画像データの解析なので次元数はRGBの3次元
som = np.random.random_sample(size=(srow, scol, 3)) # map construction

#端末依存性によらない乱数発生シードを定義する
np.random.seed(0)

#初期場を作る
ii=0
jj=0
for ii in range(srow):
    for jj in range(scol):
        #np.random.randomは0.0以上1.0未満の範囲で連続一様分布で乱数発生する
        som[ii][jj]= np.random.random(3)#()内の3は3つだけ乱数を発生する意味
#初期のSOMマップ
plt.imshow(som)

下図の初期場が構築される。

データのインポートと正規化

#画像データをインポートする
from PIL import Image
import numpy as np

im = np.array(Image.open('kingfisher.png'))
row=75
col=80

#画像データを正規化する
im_nol=im/255

#正規化した入力データを確認
plt.imshow(im_nol)

下図のように表示される。

SOMの初期設定

学習率、近傍ユニット数、学習回数を設定しておく。

#学習回数
T=10
#近傍ユニット数
unit=2
#学習率0<a<1
a=0.3
#ユークリッド距離・マンハッタン距離用のサイズを定義しておく
e_dis = np.random.random_sample(size=(row, col,1)) # map construction
m_dis = np.random.random_sample(size=(srow,scol,1)) # map construction

#カウンターなどの初期化
min_e_dis=1
min_ii=0
min_jj=0
min_si=0
min_sj=0

SOMの実行

for step in range(T):
    ii=0
    jj=0
    si=0
    sj=0
    min_ii=0
    min_jj=0
    min_si=0
    min_sj=0
    for ii in range(row):
        for jj in range(col):
            #入力データに類似する勝利ユニットを探索する####################################
            min_e_dis=1
            for si in range(srow):
                for sj in range(scol):
                        r,g,b=im_nol[ii,jj]
                        sr,sg,sb=som[si,sj]

                        e_dis[ii,jj,0]=np.sqrt( (r-sr)**2 + (g-sg)**2 + (b-sb)**2)
                        if  (e_dis[ii,jj,0]<min_e_dis) :
                            min_e_dis=e_dis[ii,jj,0]
                            min_ii=ii
                            min_jj=jj
                            min_si=si
                            min_sj=sj
                            #print(min_si,min_sj,min_e_dis)
            #########################################################################################
            sii=0
            sjj=0
            for sii in range(srow):
                for sjj in range(scol):
                    #マンハッタン距離
                    m_dis[sii][sjj]=abs(sii-min_si)+abs(sjj-min_sj)
                    allowrange=(1-(step/T))*unit
                    #print(si,sj,unitdis[si,sj,0])
                    if(m_dis[sii,sjj,0]<=allowrange):
                        #print(sii,sjj,unitdis[si,sj,0])
                        #print("update",sii,sjj)
                        som[sii,sjj,0]+=(im_nol[min_ii,min_jj,0]-som[sii,sjj,0])*a*(1-((step+1)/T))
                        som[sii,sjj,1]+=(im_nol[min_ii,min_jj,1]-som[sii,sjj,1])*a*(1-((step+1)/T))
                        som[sii,sjj,2]+=(im_nol[min_ii,min_jj,2]-som[sii,sjj,2])*a*(1-((step+1)/T))
            #########################################################################################
    print("step",step)
    fname="som_"+str(step)+".png"
    plt.title(fname)
    plt.imshow(som)
    plt.savefig(fname)
plt.imshow(som)

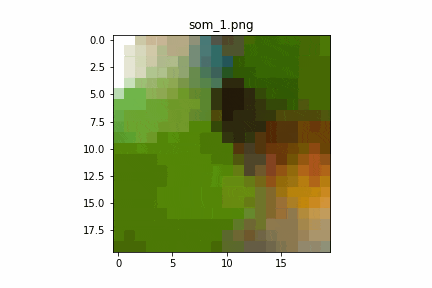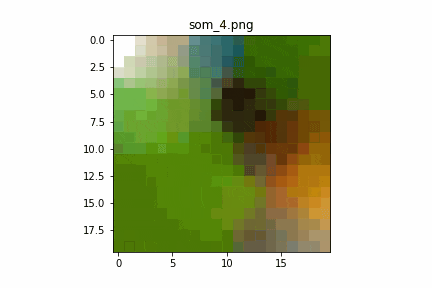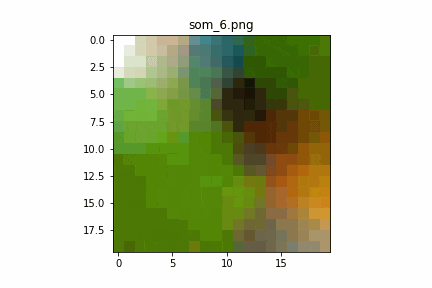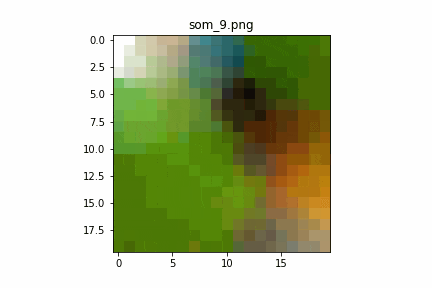
学習回数に対するSOMの変化

学習回数1回目で既にカワセミの写真が分解され、
類似したデータがまとまっているように感じます。
それ以降はサチュレーションしている感じが見て取れます。

アニメーション作成のサンプルコード

#必要に応じてpillowをインストールください
!pip install pillow
#ライブラリのインポート
from PIL import Image
#リスト作成
pictures=[]
#画像を箱に入れていく
for i in range(9):
    pic_name='som_' +str(i+1)+ '.png'
    img = Image.open(pic_name)
    pictures.append(img)
#gifアニメを出力する
pictures[0].save('anime.gif',save_all=True, append_images=pictures[1:],
optimize=False, duration=500, loop=0)

まとめ

自己組織化マップは教師なし学習の手法であり、
多次元情報を視覚的に整理する際に有効な手段であると考えます。
機会があれば、分類の問題で自己組織化マップの活用記事などを書こうと思います。
最後までお読みいただきありがとうございました。