はじめに
筆者はPythonならびにAIの初学者で、Aidemy Premiumの「データ分析3ヶ月コース」を受講しながらデータ分析について学習をしています。
講座内で学習した知識をもとに自身で時系列解析の実装・考察を行っていきます。
自己紹介
・2人目の子供を妊娠中の30代女性
現職は損害保険会社勤務でプログラミングやAIについての知識ゼロから、
出産までの休暇期間を利用して学習を行っています。
家族が増えることに伴い、より柔軟な働き方にチェンジしたいと思い、
自身の興味関心・やりたいことは何かを考えた結果、
AI学習やデータ分析にたどり着きました。
今回は受講の修了要件の1つである成果物としてこのブログを執筆しています。
受講修了後も今後のキャリアチェンジのために、産後もコツコツと継続して学習を行っていく予定です。
テーマと分析方法
普段子供の服を海外から個人輸入することがあったり、
そろそろ海外旅行に行きたいなという気持ちがあったりで、
最近よくドル円の為替を見ていたのですが、
2022年、一時は1ドル=150円の歴史的な円安に達してびっくり。(ここまでの円安は32年ぶり!)
今後個人輸入するタイミングはいつか、海外旅行に行くならいつ頃かを予測したいと思い、
過去の時系列データからドル円為替を予測するプログラムを作成することにしました。
時系列解析の分析にはSARIMAとLSTMの2種類の方法を採用し、比較を行いたいと思います。
実行環境
Google Colaboratory
Python 3.8.16
実装(SARIMA/LSTM共通部分)
step1 データの取得
データの取得にはpandas-datareaderモジュールを使用することにしました。
DataReader(stock_code, source, start, end)の形式でデータを取得します。
import pandas_datareader.data as pdr
import numpy as np
import datetime as dt
start = dt.datetime(1971,1,4)
end = dt.datetime(2022,11,30)
JPY_USD = pdr.DataReader('DEXJPUS', 'fred', start, end)
step2 時系列データの視覚化
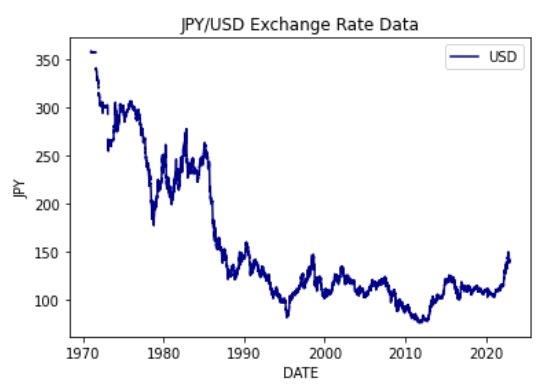
どのようなデータが取得できたのかを折れ線グラフで描写して確認します。
import matplotlib.pyplot as plt
plt.title("JPY/USD Exchange Rate Data")
plt.xlabel("DATE")
plt.ylabel("JPY")
plt.plot(JPY_USD, color='darkblue', label="USD")
plt.legend()
plt.show()
step3 データの前処理
step3.1 データの切り取り
過去15年分のデータを利用することにして、データの切り取りを行います。
JPY_USD1 = JPY_USD.loc["2007-12-01":]
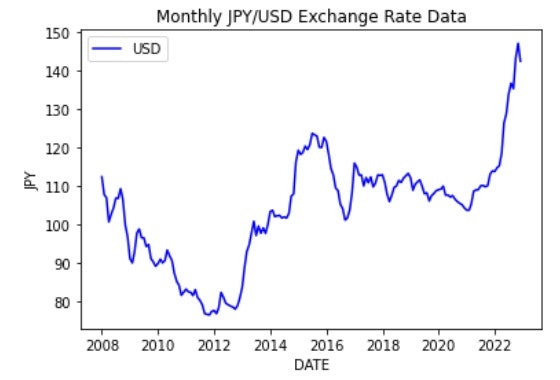
step3.2 日次データを月次データに変換
JPY_USD1.columns = ["Exchange Rate"]
Monthly_JPY_USD = JPY_USD1.resample("M").mean()["Exchange Rate"]
plt.title("Monthly JPY/USD Exchange Rate Data")
plt.xlabel("DATE")
plt.ylabel("JPY")
plt.plot(Monthly_JPY_USD, color='b', label="USD")
plt.legend()
plt.show()
実装(SARIMA)
step4 パラメーターの決定
PythonにはSARIMAモデルのパラメーター、(p, d, q) (sp, sd, sq, s)を自動で最も適切にしてくれる機能はありません。
そのため 情報量規準 (今回の場合は BIC(ベイズ情報量基準) )によってどの値が最も適切なのか調べるプログラムを書きます。
BICの場合は、その値が低ければ低いほどパラメーターの値は適切であると判断します。
パラメーターsに関しては、本来は事前に時系列データや偏自己相関の可視化を行うことによって調べておく必要があるのですが、今回は12ヶ月と仮定します。
import itertools
import statsmodels.api as sm
def selectparameter(DATA,s):
p = d = q = range(0, 2)
pdq = list(itertools.product(p, d, q))
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
parameters = []
BICs = np.array([])
for param in pdq:
for param_seasonal in seasonal_pdq:
try:
mod = sm.tsa.statespace.SARIMAX(DATA,
order=param,
seasonal_order=param_seasonal)
results = mod.fit()
parameters.append([param, param_seasonal, results.bic])
BICs = np.append(BICs,results.bic)
except:
continue
return parameters[np.argmin(BICs)]
best_params = selectparameter(Monthly_JPY_USD,12)
print(best_params)
以下の通り、最適な(p,d,q),(sp,sd,sq,s)が求められます。
[(1, 1, 0), (0, 1, 1, 12), 794.6119679719479]
step5 モデルの構築
モデルの構築にはsm.tsa.statespace.SARIMAX(DATA,order=(p, d, q),seasonal_order=(sp, sd, sq, s)).fit()を用います。
SARIMA_Monthly_JPY_USD = sm.tsa.statespace.SARIMAX(Monthly_JPY_USD,order=best_params[0],seasonal_order=best_params[1]).fit()
step6 予測
モデル名.predict("予測開始時","予測終了時")とすることで予測データが得られます。
pred = SARIMA_Monthly_JPY_USD.predict("2021-12-31","2025-11-30")
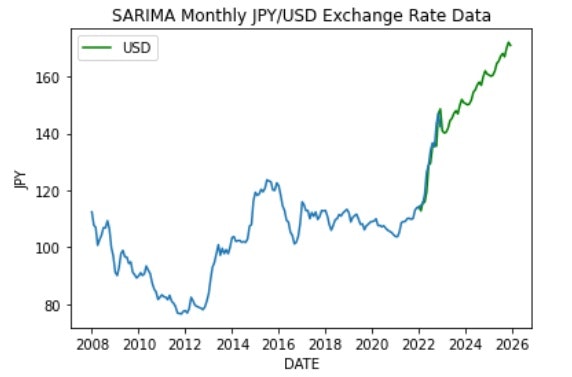
plt.title("SARIMA Monthly JPY/USD Exchange Rate Data")
plt.xlabel("DATE")
plt.ylabel("JPY")
plt.plot(pred, color="g", label="USD")
plt.plot(Monthly_JPY_USD)
plt.legend()
plt.show()
実データと予測データはFITしているようです。
未来の予測部分は直近の円安を反映したのか、総合的にかなりの右肩上がりとなりました。
(こんなに円安が進んでしまうと海外旅行は夢のまた夢です。)
実装(LSTM)
step3 データの前処理(続き)
step3.3 時系列データの値のみを取り出す
今回のLSTMによるデータ予測では、ある時点からいくつか前のデータを用いて次の時点のデータを予測するモデルを作成するので、用意されたデータから時系列データの値のみを取り出します。
print(Monthly_JPY_USD)
元のデータは以下の通りです。
DATE
2007-12-31 112.449000
2008-01-31 107.818095
2008-02-29 107.030000
2008-03-31 100.756190
2008-04-30 102.677727
...
2022-07-31 136.709000
2022-08-31 135.283478
2022-09-30 143.284286
2022-10-31 147.051500
2022-11-30 142.445000
Freq: M, Name: Exchange Rate, Length: 180, dtype: float64
時系列データの値のみを取り出します。
input_data = Monthly_JPY_USD.values.astype(float)
step3.4 データのスケーリング
データを0~1に正規化します。
与えられたデータをすべて用いてスケーリングしてしまうと、訓練データに検証データの情報が混入してモデルがデータに適合し過ぎてしまい、実際のデータを与えた際に予測精度が低くなるため注意が必要です。
よって、スケーリングは訓練データのみを基準に行います。
train_size = int(len(input_data) * 0.90)
norm_scale = input_data[:train_size].max()
input_data /= norm_scale
print(input_data[0:5])
先頭5行を出力して確認します。
[0.90890915 0.87147821 0.86510814 0.81439784 0.82992935]
step4 入力データ・正解ラベルの作成
基準となる時点からいくつか前のデータを用いて次の時点のデータの予測を行います。
今回は3つ前のデータまでを利用することにします。
また、データをLSTMで分析できるデータ形式に整形します。
def make_dataset(low_data, maxlen):
data, target = [], []
for i in range(len(low_data)-maxlen):
data.append(low_data[i:i + maxlen])
target.append(low_data[i + maxlen])
re_data = np.array(data).reshape(len(data), maxlen, 1)
re_target = np.array(target).reshape(len(data), 1)
return re_data, re_target
window_size = 3
# 入力データと正解ラベルへの分割
X, y = make_dataset(input_data, window_size)
print("shape X : " , X.shape)
print("shape y : " , y.shape)
step5 訓練データ・検証データの作成
時系列データにはある程度の周期性や連続性が存在するため、ランダムに分けてしまうと、これらの情報を破棄してしまうことになります。
今回は元データをのうち、前半の90%をトレーニング用、残りの10%をテスト用に分けます。
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
step6 モデルの構築
80層のLSTMと出力層のみによるモデルを構築します。
import keras
from keras.models import Sequential
from keras.layers import Dense, Activation, LSTM
from keras.optimizers import Adam
import tensorflow as tf
lstm_model = Sequential()
lstm_model.add(LSTM(80, batch_input_shape=(None, window_size, 1)))
lstm_model.add(Dense(1))
lstm_model.compile(loss='mean_squared_error', optimizer=Adam() , metrics = ['accuracy'])
step7 予測
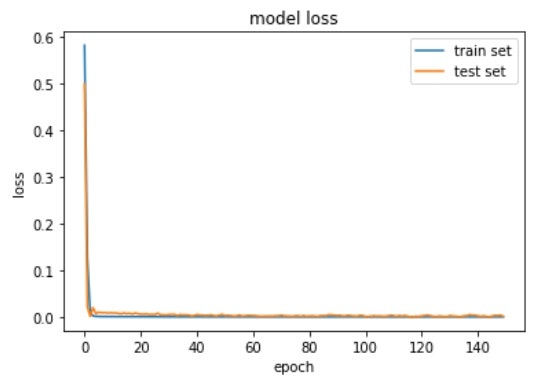
コンパイルしたモデルを学習させます。今回は150エポックで学習させました。
学習が収束していることを確認するため、エポックごとの損失の推移もプロットします。
batch_size = 10
n_epoch = 150
hist = lstm_model.fit(X_train, y_train,
epochs=n_epoch,
validation_data=(X_test, y_test),
verbose=0,
batch_size=batch_size)
# 損失値(Loss)の遷移のプロット
plt.plot(hist.history['loss'],label="train set")
plt.plot(hist.history['val_loss'],label="test set")
plt.title('model loss')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend()
plt.show()
損失の推移は以下の通りです。収束していることが確認できます。
検証データの予測を行います。
y_pred_train = lstm_model.predict(X_train)
y_pred_test = lstm_model.predict(X_test)
# RMSEで評価
def rmse(y_pred, y_true):
return np.sqrt(((y_true - y_pred) ** 2).mean())
print("RMSE Score")
print(" train : " , rmse(y_pred_train, y_train))
print(" test : " , rmse(y_pred_test, y_test))
# 推定結果のプロット
plt.plot(X[:, 0, 0], color='blue', label="observed") # 元データ
plt.plot(y_pred_train, color='red', label="train") # 予測値(学習)
plt.plot(range(len(X_train),len(X_test)+len(X_train)),y_pred_test, color='green', label="test") # 予測値(検証)
plt.legend()
plt.xticks(np.arange(0, 169, 12)) # 12ヶ月ごとにグリッド線を表示
plt.grid()
plt.show()
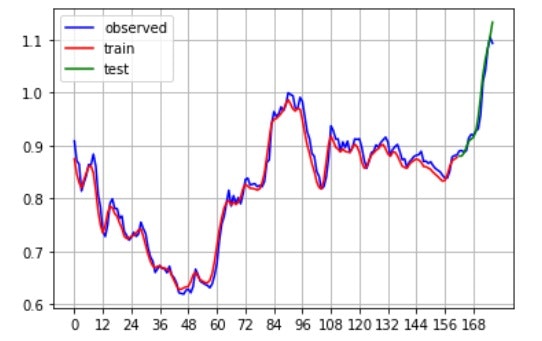
RMSEと予測結果のグラフは以下の通りです。
円安の山が少しずれる部分はありますが、学習結果はおおむね良好そうです。
6/6 [==============================] - 0s 3ms/step
1/1 [==============================] - 0s 16ms/step
RMSE Score
train : 0.02893243288232912
test : 0.05719647536949624
step8 未来予測
学習したモデルを用いて未来の時系列を予測してみます。
予測でも直近3ヶ月分のデータを参照して次の1ヶ月の予測を行い、これを繰り返していきます。
import matplotlib.dates as mdates
# 予測結果を保存する行列
future_pred = X[:,0,0].copy()
# 予測期間は観測値の終端から3年間を設定
pred_time_length = 12*3
for tmp in range(pred_time_length):
# 観測結果の最後尾から予測に使うデータをピックアップ
X_future_pred = future_pred[-1*window_size:]
# 予測
y_future_pred = lstm_model.predict( X_future_pred.reshape(1,window_size,1) )
# 予測値をfuture_predの最後尾に追加
future_pred = np.append(future_pred, y_future_pred)
#print(y_future_pred , future_pred[-5:])
import pandas as pd
date = pd.DataFrame(Monthly_JPY_USD.index)
inp = pd.DataFrame(input_data, columns=["DATA"])
input = pd.concat([date, inp], axis=1)
input.index = input["DATE"]
input=input.drop(columns="DATE")
DATE = []
for idx in range(37):
if idx in [i for i in range(0,12)]:
DATE.append(dt.datetime(2023, idx+1,28))
elif idx in [i for i in range(13,25)]:
DATE.append(dt.datetime(2024, idx-12,28))
elif idx in [i for i in range(25,37)]:
DATE.append(dt.datetime(2025, idx-24,28))
dfp = pd.DataFrame({"DATE":DATE, "DATA":future_pred[-1*pred_time_length:]})
# プロット
# 実測値
plt.plot(input.index, input["DATA"] * norm_scale, color='blue', label="observed")
# 予測値
plt.plot(dfp["DATE"], future_pred[-1*pred_time_length:] * norm_scale, color='red', label="feature pred")
plt.grid()
plt.show()
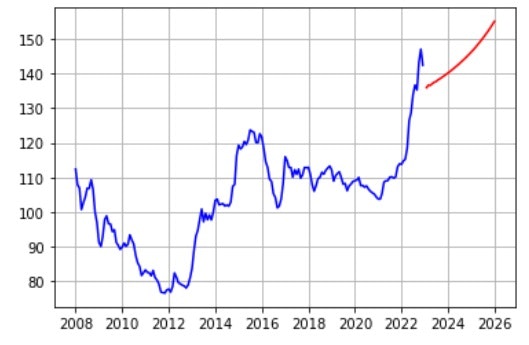
予測結果は以下の通りです。
SARIMAよりは上昇は抑えられているもののこちらも右肩上がりでした。
考察・反省
SARIMAとLSTMいずれも検証データの学習結果まではおおむね良好でしたが、
未来予測となると過去の時系列データを参照するだけでは難しいものがあるなと感じました。
特にLSTMに関しては、直近3ヶ月のデータを元に予測を行っているため、実測値の円安の影響を反映して直線的な右肩上がりとなってしまったようです。
過去のデータのみで予測が難しい為替変動については、他の説明変数(日米の金利差、平均賃金、物価など)を加えて分析することが必要なようです。
今後はそういった他の説明変数を加えた分析の実装にも取り組んでいきたいです。