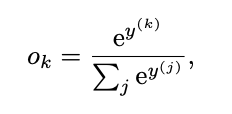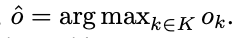Learning to Play Othello with Deep Neural Networks といういかにも面白そうな論文の日本語訳です。
Wojciech Jaskowski 氏らに許可をいただいて公開しています。
なお、原文では VI-B の図 IV が欠けていますが、Wojciech Jaskowski 氏から直接提供いただき許可を得て掲載しています。
また、脚注については原文を参照して下さい。
筆者の勉強不足で解釈の怪しいところがあるかもしれません。詳しい方は Pull Request 送ってもらえると助かります🙏
以下翻訳。
概要
AlphaGo による超人的なプレイレベルの達成は、複雑な空間パターンをデータとして保存できる CNN の威力を裏付けました。
この結果は、「囲碁の盤面状態」と「いままで CNN の対象になってきた 2D 画像」との間にある、いくつかの類似点が大きな要因でした。とりわけ、囲碁の大きな盤と並進不変性との間にある類似性に起因していました。
この論文では、CNN ベースの着手予測子がオセロに対して効果的であるかどうかを検証します。オセロは、盤面サイズが遥かに小さくて並進不変性が無いので、囲碁とは性質が全く異なるゲームです。
いくつかの CNN アーキテクチャとボードエンコーディングを比較し、それらを最先端の拡張機能で補強し、エキスパートたちの幅広いデータで訓練します。そして、着手の正確性と棋力について調べます。
今回の実験で得られた結果は、ニューラルな着手予測子の高い能力を裏付けており、予測精度と棋力の間に強い相関関係があることを示唆しています。
最高の CNN は、これまでに提案されてきた他の全ての 1-ply オセロソフトを上回るだけでなく、最高のオープンソースである Edax (の 2-ply) をも打ち負かします。
索引用語
deep learning, convolutional neural networks, Othello
著者は、ポーランドの Poznan にある Poznan 工科大学のコンピューティングサイエンス研究所に所属しています。
W. Jaskowsk が、スイスの Manno TI にある IDSIA Dalle Molle Institute for Artificial Intelligence Research に籍を置いてる間に、今回の研究を行いました。
I. 導入
ニューラルネットワーク、特に深い CNN は、あらゆる種類に対応しうると言ってもいいくらいに、優れたパターン認識能力を持っています。[32]
CNN は自然と任意の次元に一般化されるので、ラスター画像、時系列、ビデオシーケンス、そして 3D ボリュームデータの分析に適しています。[38]
このような性質を持つ CNN は、様々な挑戦的なタスクに対して、前例のないパフォーマンスレベルを発揮することが可能です。画像分類[12]、オブジェクトのローカライゼーション[10]、オブジェクト検出[27]、画像セグメンテーション[23]、さらには 3D 環境下での視覚的な強化学習[19] などで活躍します。
2D ラスター画像とゲームにおける盤面状態との構造的な類似性は自然なものなので、過去にニューラルネットワークのパラダイムで利用されてきたのも不思議ではありません([42]など)。
ただし、ほとんどの場合、ニューラルネットはゲームツリーの検索に使用される評価関数として機能していました。
これまで人間しか到達できないと考えられていたプレイレベルを、直接的な着手予測子として実現可能になったのはごく最近のことです。これは、深い CNN に活用可能な大規模コンピューティングや効率的な学習アルゴリズムのおかげです。
これにより、超人レベルの囲碁プログラムである AlphaGo という最高な成果を含む、一連の囲碁プログラムが誕生しました。
囲碁プレイヤーは、数手先までの "具体的な" 着手を読むことよりも、盤面状態のパターン検出に強く頼っていることが長い間知られていたため、囲碁における CNN は成功に至りました。
ツリー検索のアプローチは、膨大な分岐数および大きな盤面サイズと相まって、囲碁に対しては非効率なのです。
ここで我々は問いかけたいと思います。
minimax スタイルのツリー検索アルゴリズムが十分に機能しており、既に人間レベルのパフォーマンスを実現しているだけでなく、分岐係数も盤面サイズも囲碁より小さいゲームに、CNN が実用的であるかどうか?
それを検証するために、長年 AI のベンチマークとなっている[18] オセロに関して、CNN ベースの着手予測子を学習することを考えました。
これは囲碁と異なるだけでなく、コンピュータビジョンにおける画像分析とも大きく異なります。
入力ラスターが小さく(8×8 のサイズで、3 値で盤面状態が表される)、一般的な現実世界のノイズや歪み(センサーノイズ、ライティング、遠近法など)がありません。また、平行移動やスケーリングではなく、軸方向の対称性という理想的な不変性を持っています。
重要なことを言い忘れましたが、盤面上の石一つ一つどれもが重要であり、着手の決定に影響を与えます。CNN がこのような状況下で評価されたことはほぼありません。
私たちが取り組む項目は以下の通りです。
- オセロのための、ニューラルネットワークの様々な CNN ベースのアーキテクチャ検証
- フランスのオセロリーグのゲームデータセット WThor による、最先端の着手予測精度
- これまでのアプローチよりも大幅に改善された、最先端の 0-ply(先読み無し)ポリシー
- 着手予測子の精度と勝率の関係、特定の盤面状態での強みと弱み、様々な深さでゲームツリー検索を使用する相手との対決など、訓練されたポリシー特性の詳細な分析
本論文で得られた成果は、提案されたニュートラルアーキテクチャのいくつかが最新の着手予測子であることを示唆します。
Ⅱ. 関連功績
CNN は、Neocognitron で Fukushima によって紹介され[9]、以降の 20 年間、いくつかの画像分析タスクに利用されてきました。[22]
しかしながら、それらをより幅広い画像分類に適用する試みは、ほとんど成功しませんでした。
最近、深層学習が台頭して重要な概念のブレイクスルーをもたらしたことで、より深く複雑なネットワークの訓練が可能になりました。
これは、GPU によって提供される安価な計算能力と組み合わさって、機械学習に革命をもたらし、前例のない分類精度の達成を可能にしました。例として ImageNet データベースで性能評価が実施された、一連のニューラルアーキテクチャが挙げられます[21],[12]。
導入で触れたように、自然の画像とゲームボードの構造的な類似性は我々人間にとって非常に明白なので、長い間見過ごされ続けることはありませんでした。
それは、ボードゲームに CNN を適用する初期の試みに繋がりました。[8]
すぐに、深層学習パラダイムが、ゲームツリー検索技術と一緒に利用できるほど強力である可能性が明らかになりました。
この考えが、最初の超人レベル囲碁プレイシステムである DeepMind の AlphaGo に繋がりました。それは、教師あり学習、ポリシー勾配検索、モンテカルロ木探索を組み合わせたものでした。
オセロは、長い間計算知能手法で人気のベンチマークでした。[29], [35], [5], [25], [26], [42], [40], [28], [16], [30], [18]
全ての強力なオセロプレイシステムは、盤面評価機能を備えた minimax 検索の変化手法を使用しています。
過去の研究では、前者よりも後者を改善することで、より多くのことが得られることが示唆されています。そのため、最近は、自己学習[26],[18]、固定の対戦相手[20]、エキスパートのゲームデータベース[30]のいずれかを使用して、1つの先読み(1-ply)エージェントの訓練に焦点が当てられることが多かったです。
これまで、エージェントを訓練する複数の方法が提案されてきました。例えば、値ベースの時間差学習[25],[42],[34]、(共)進化[26],[31],[17],[15]、及びそのハイブリッド[39][40]。
盤面評価関数の設計には、適切な関数近似器を見つける必要があります。
ボードゲームで最も成功している関数近似器の 1 つは、N タプルネットワークです。
興味深いことに、それらはもともと光学式文字認識[4]のために提案されたものであり、ボードゲームへの適用は、ボードゲームの盤面と画像との間に類似性がある可能性を示していました。
それは、Buro により作られた有名な Logistello プログラムで、tabular value function と名付けられてオセロに採用され、後に Lucas[24] によって普及しました。
ニューラルネットワークは、例えば[42]で、関数近似器としてオセロにも使用されていますが、我々の知る限り、CNN がこの目的で使用されたことはありません。
我々は、オセロ向けに公開された着手予測子をいまだ知らないため、この論文の実験部分では、その方法を 1-ply 戦略の代表的なサンプルと比較します。
オセロの最先端の 1-ply プレイヤーの比較は[18]にあります。
公開されている功績では、最高の 1-ply プレイヤーは、共進化 MA ES (共分散行列適応進化戦略)[18]と体系的な N タプルネットワークによって得られたようです。
複数のオセロプログラムの中で、現代のリーダーの 1 つが Edax です。Edax は、ゲームの各段階で 1 つずつ、tabular value function を使用するオープンソースのプレイヤーシステムです。
Edax は高度に最適化されており、ディープツリー minimax のような検索(Multi Prob Cut を使用した NegaScout)を使用します。
残念ながら、その評価関数がどのように実現されたかについての説明は公開されていません。
これまでのオセロプレイヤーのトップ 5 の 1 つは、RL14_iPrefN で、フランスのオセロリーグエキスパートゲームデータセット[30]を順序学習して訓練されており、53.0 % の分類精度が得られたと報告されています。
この論文では、このベースラインを大幅に上回ります。
Ⅲ. オセロ
オセロは、8×8 ボードでプレイされる、二人零和有限確定完全情報ゲームです。
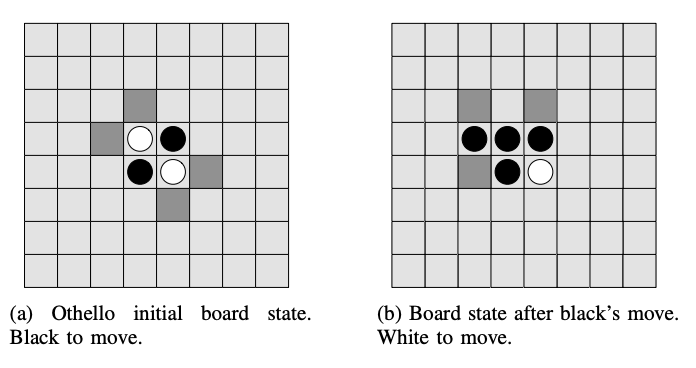
片手番が白、相手番が黒で、64 個の石があります。ゲームは、各プレイヤーが盤面の中央に 2 つの石を斜めに配置することから始まります。(図 1a)
黒のプレイヤーが最初に着手し、4 つの影付きの場所のいずれかに石を置きます。これにより、例えば図 1b の盤面状態になります。
新しく配置する石が、対戦相手の石に隣接し、1 つまたは複数の相手の石を水平,垂直または対角線上で両側から囲める場合、その着手は合法手になります。
着手したら、挟んだ石を裏返します。そして、プレイヤーは交互に石を置いていきます。
どちらのプレイヤーにも合法手がなくなった時にゲームは終了し、盤面上により多くの石があるプレイヤーの勝ちとなります。もし両プレイヤーの石数が同数であった場合、ゲームは引分となります。
このように単純なルールではありますが、オセロのゲーム性は決して薄くありません。
盤面状態の数は、およそ 10^28 であり、ゲームツリーとしては 10^58 空間量があります。[1]
そのため、しらみつぶしな探索手法は難しいです。
そしてまた、オセロは、時間的な変動性が大きいという特徴もあります。1 回の着手で多数の石が反転することがあり、盤面の状態が劇的に変化するのです。
これらの特徴と、ゲームがまだ完全に解析されていないという事実により、オセロは計算知能手法にとって興味深い実験台となっています。
IV. エキスパートの着手を予測するための学習
A. 分類問題
オセロは、決定論的で、完全に観測可能なゲームです。
そのため、ポリシー π: X->Y については、盤面状態が X、着手アクションの空間が Y = {1,...,K} になります。Y は盤面の全マス 1 つずつに対応します。
π(x) は、盤面状態 x ∈ X に対する望ましい着手を意味します。
X×Y における良い(エキスパートの)着手の N 個の訓練データセットを与えられた時、多クラス分類問題として π を見つける問題と捉えらることができます。
このような問題への典型的なアプローチは、パラメータ化された確率関数 p(y|x;θ) を訓練することです。これは、状態 x で y を着手する信頼度を表します。
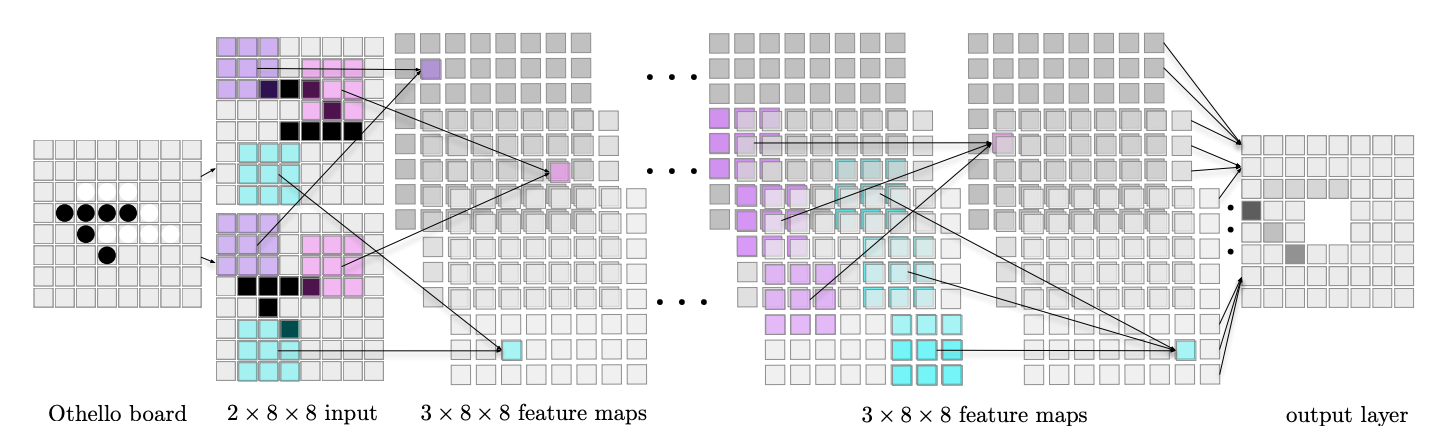
図Ⅱ: 着手予測子のための例示的な CNN。盤面は、8×8 の 2 チャンネルバイナリー画像としてネットワークに送られます。最初のチャンネルが片手番の石、2 番目のチャンネルが相手番の石を示します。特徴マップ(色付きの正方形)のユニットは、画像(あるいは前のレイヤー)の 3×3 RF (同じ色)からデータを受信します。ネットワークはエッジにゼロ埋めを使用(図示はされていません)しているため、全てのレイヤーのマップは 8×8 です。分かりやすくするために、各隠れ層には 3 つの特徴マップしかありません。
p を推定するには、交差エントロピー誤差を最小化する必要があります。
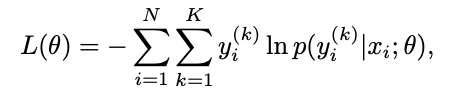
ここで、y = k の場合は y(k) = 1、それ以外の場合は 0 です。訓練アルゴリズムのゴールは、最適な θ を推定し、L(θ) を全体最適解に十分近づけるポリシーパラメータである ^θ を見つけることです。
一度見つかったら、プレイヤーは最高の信頼度を持つ着手を選択します。
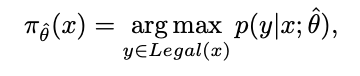
ここで、Legal(x) ⊂ Y は、盤面状態 X における合法手の部分集合です。
π が、数手先の進行に関する明示的なシミュレーション(例えば、minimax スタイルのアルゴリズムを使用したシュミレーション)なしで着手を決定する場合、それを着手予測子と呼びます。
オセロの盤面上のマスと着手は 1 対 1 で対応しているので、着手予測子の設計がとても容易です。
ボード外に着手可能な異種の駒を含む他のボードゲームの場合、着手 Y の空間はより複雑であり、より洗練された表現が必要になってしまいます。
B. 着手予測のための CNN
最も単純なシナリオは、X の盤面状態を 64 個の 3 値変数としてエンコードし、任意の確率評価器に入力することです。
ただし、一般的な確率評価器は、オセロの盤面状態のような類の構造には向いていません。
それを理解するには、盤面上の石がランダムに並び替えられた場面を想像するだけで十分です。
その状況は、人間にとってゲームが完全に難読化された状態であると言えます。(ただし、前のセクションで示した式の下では、依然として同じポリシーの学習タスクなのです)
これは、手番及び相手番の石配置の空間パターンを観測することが不可欠であることを示しており、そのような機能を備えた学習システムを利用すること、つまり盤面状態を画像として扱うことが適切です。
以下では、オセロの着手予測子のために調整された CNN アーキテクチャについて簡単に説明します。また、このトピックに関心のある読者に向けて他の研究も包括的に紹介します。[2][32]
話を分かりやすくするために、ここではコアとなる CNN アーキテクチャのみを示し、次の実験セクションで拡張的な内容を付け加えることにします。
CNN は、複数の基本処理ユニットの複合体であり、それぞれに重み付き入力と 1 つの出力が備わっており、入力信号を重み付きで畳み込み、非線形なフォーマットで結果を変換します。
ユニットは矩形の特徴マップ(グリッド)に配置され、入力画像のラスターと空間的に整列されます。ユニットの空間配置は、CNN が視覚情報の処理に適す理由の 1 つです。
特徴マップはレイヤーに配置され、特定レイヤーのマップは、前のレイヤーからの信号のみを取得します。(図2も参照)
我々の CNN は、現在の盤面状態を 2 つの 8×8 バイナリ行列にエンコードされた入力として受け取ります。
1 つ目は手番側の石配置を表す行列、2 つ目は相手番側の石配置を表す行列です。
このエンコーディングを pices と呼ぶことにします。
また、vmoves と呼ぶことにするエンコーディングでは、ゲームプレイ中に合法手を簡単に選択できるように、プレイヤーの合法手をマークしておく行列を追加します。
囲碁[33]で行われた最近の調査に従い、我々は、pices だけを含む正則化チャンネルを追加したエンコーディングも定義することにします。
上記の方法で表現された盤面状態は、2 つ(pieces の場合)あるいは 3 つ (vmoves と pieces の場合)のチャンネルで構成される 8×8 のバイナリイメージを形成し、CNN 第 1 層の特徴マップによって取得されます。
特徴マップの各ユニットは、受容野(RF)、すなわち隣接するマスの小さな矩形からのみデータを受信しますが、全てのチャンネルからデータを受信してチャンネルごとに個別の重みセットを使用します。(図2 の RF の例を参照)
後続のレイヤーでも同様に、ユニットは前のレイヤーの全ての特徴マップの対応する RF からデータを取得し、それらを個別の重みセットで処理します。
特徴マップ内の隣接するユニットの RF は、ストライドによってオフセットされます。盤面サイズ、RF サイズ、そしてストライドが一緒になって特徴マップの次元を決定します。
例えば、ストライド 1 の 3×3 RF を備えた特徴マップは、8×8 盤面に適用した場合、36 ユニットしか必要としません。なぜなら、幅 3 の 6 つの RF で 2 列ごとに重複し、盤面全体の横幅(そして高さ)に跨がるためです。
局所的な接続性により、重みの数が大幅に削減され、空間パターンのキャプチャが容易になります。
同じ特徴マップ内のユニットは重みを共有するため、盤面の異なる部分からとはいえ、同じ局所的な特徴を計算します。
これにより、パラメータの数がさらに減り、抽出された特徴が同変となります。
例えば、上記の 6×6 の特徴マップには、b 個のチャンネル入力に対して、9×(b + 1) のパラメータしかありません。(「3×3 = 9」+「特徴マップごとに 1 つの閾値」)
我々は、非線形性を f(x) = max(x, 0) と定義しつつ、正規化線形ユニット(ReLU)を使用して畳み込みの結果を処理します。
ReLU は、squeezing-function ユニット(例えば シグモイド関数や tanh 関数)よりも早くネットワークを学習させることができ、多層ネットワークで特に効果的です。
そのため、勾配が全ての正の excitation に対して誤差逆伝播するため、勾配消失問題を効果的に軽減します。これは squeezing ユニットでの小さな excitation 間隔とは対照的です。
我々の基本的なアーキテクチャは、表Ⅰに示した 4, 6, そして 8 つの畳み込み層で構成されるネットワークです。
表Ⅰ: 実験で使用された CNN アーキテクチャ。層の命名は、特徴マップの数に従っている。

各アーキテクチャでは、入力は、3×3 RF とスライドが 1 に設定された、64, 128 あるいは 256 の特徴マップで構成される畳み込み層のスタックを通過します。
入力は非常に小さいため、畳み込み後の空間解像度を維持するために、グリッドの境界をゼロ埋めします。(RF が入力グリッドを超えて到達できるようにする)
同じ理由で、小さな入力グリッドの場合は理論的な根拠が少ないため、畳み込み以外の方法で複数ユニットの出力を集約するなどのいかなる形式のプーリングを行わないことにします[36]。
したがって、全レイヤーの全ての特徴マップは 8×8 ユニットになります。
全てのアーキテクチャで、畳み込み層(conv)のスタックの後に 2 つの全結合層(fc)が続きます。
隠れ層は、ReLU による活性化を備えた 128 ユニットで構成され、出力層は着手候補 60 個に対応する K = 60 のユニットを持ちます。
各出力 y(k) は、単一の局面に対応し、必要な着手はバイナリ 1 of K エンコーディング(one-hot エンコーディング)を用してエンコードされます。
出力値を確率として解釈するには、合計を 1 にする必要があります。これは、 softmax 変換を使用して実現されます。
表Ⅰに示されているアーキテクチャは、一連の予備実験の結果です。畳み込み層を 8 より多くしても、訓練時間が大幅に長くなるだけで、パフォーマンスは向上しないことが分かりました。
また、実行時間と精度とのトレードオフを考慮すると、大きな RF を使用するよりも、小さな 3×3 RF + 深いネットワークの方が効率的であると判明しました。
V. 着手予測精度の実験
A. 実験のセットアップ
このセクションでは、ネットワークを着手予測子と見なし、実際のゲームには関与させません。
主要なパフォーマンス指標は、予測精度、つまりは正確に予測された着手の割合です。
後述のセクションⅣで説明しますが、我々は、人間のプレイしたゲーム(セクションV-A2を参照)から抽出されたデータセットで訓練された、様々な着手予測子の構成を比較します。
1) データセット
1985 年に作成された、WThor データベース 2 には、フランスの様々なトーナメントで行われたエキスパートプレイヤーの試合が 119,339 個含まれています。
我々は、それらの記録から、手番プレイヤーの盤面状態と、プレイヤーが選択した着手を添えた、全ての状態を抽出しました。
結果として得られた、盤面(board),色(color),着手(move)の 3 値から成る 6,874,503 のセットを、Original と呼ぶことにします。
次に、重複を削除したところ、4,880,413 のセットを得ました。これを、Unique と呼ぶことにします。
両方のデータセットに、一貫性のないデータが含まれうる点に注意して下さい。具体的には、異なる着手に関連づけられた同じ盤面状態のことです。
完全な分類器は、Original で 91.16 %、Unique で 97.49 % の精度を達成できます。
color 属性は、白手番が着手する時に盤面上の石を反転するためだけに使われます。これにより、データセット内の全ての状態を、黒手番視点で表現できるのです。
深層学習は、とりわけ大量のデータで訓練した場合にパフォーマンスを発揮することが知られています。
そこで、データセットを拡張するために、オセロの対称性を利用します。
Original と Unique データセットの盤面状態それぞれについて、7 つ全ての反射と回転を施したセットを生成します。
これにより、それぞれ 2 つの対称なデータセットが生成されます。Original-S (54,996,024 のセット)と、Unique-S (39,019,056 のセット)で、後者では対称変換から生じる重複も解消してあります。
着手予測子を一般的化した際の能力を評価するために、各データセットを互いに素な訓練セットとテストセットに分割しておきます。
非対称データセット(Original と Unique)の場合、テスト用に 25 % のセットを割り当てることにします。
対称データセットは遥かに大きいため、テストに割り当てる例は 5 % のみで十分で、全てのテストセットのサイズは同じです。
2) 訓練
訓練には、0.95 の momentum を持つ確率的勾配降下法を使用します。
ユニットの重みは[11]の方法を使用して初期化し、バイアス(オフセット)は 0 で初期化します。
学習率は最初は 0.1 に設定し、その後 epoch ごとに 2 度半分にします。
損失関数は、5 * 10^-4 の重みを持つ L2 ノルムによって正則化されます。
非対称データセット(171, 600 バッチ)の場合は 24 epoch 後に、対称データセット(434, 400 バッチ)の場合は 6 epoch 後に学習を停止します。
実装は、単精度演算で GPU 上の全ての計算を実行する Theano フレームワーク[41]に基づいています。
実験は、NVIDIA GTX TitanGPU を搭載した IntelCore i7-4770KCPU で実施しました。
訓練時間は構成に応じて 1~10 h まで変化させました。Unique-S で訓練された Conv8 は約 62 時間でした。
B. 結果
1) データ拡張の効果
表Ⅱ: 4 つの異なる訓練セットで訓練されて Original テストセットでその成果を評価された、ネットワークの予測精度です。pices エンコーディングが使用されています。

表Ⅱは、pices エンコーディングを使用して特定の訓練セットで訓練された、基本的なアーキテクチャ 3 つの予測精度を示しています。
公平を期すために、ネットワークは同じデータ、つまり Original テストセットで評価して比較します。
対称性によって拡張されたデータセットでの訓練は、高い予測精度をもたらします。
重複削除の影響はさほど大きくありませんが、一貫して予測精度にポジティブに働きます。
これら 2 つの傾向が相まって、Unique-S が最も有望なデータセットなので、次の実験ではそれのみを使用します。
2) ボードエンコーディングとレイヤー数の影響
表Ⅲ: 様々なボードエンコーディングと畳み込み層の数に対する、Unique-S テストセットの予測精度
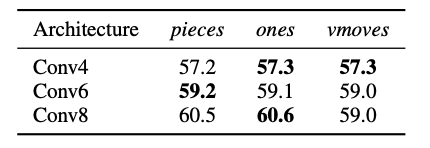
表Ⅲは、盤面状態の様々なエンコーディングを使用して Unique-S で訓練した場合の、3 つのアーキテクチャの予測精度を示しています。
今回は Unique-S テストセットでネットワークをテストします。これは、Original テストセットがテストに使用された表Ⅱと比べて小さな違いを示します。
精度は明らかにレイヤー数と相関関係があるので、より深いアーキテクチャに手をのばしたくなります。
ただし、Conv8 に類似した 10 層アーキテクチャでは、予測精度を向上させることができませんでした。
エンコーディングの比較に関しては、pieces は同等に機能しているように見えました。そのため、追加のレイヤーやチャンネルを必要としない、前者(Conv8)を優先するべきです。
vmoves の相対的なパフォーマンスの低下は不可解です。なぜなら、学習者に着手の有効性についてのヒントを与えることが、どのようにパフォーマンスの低下をもたらすのか理解しがたいためです。
この結果を調査する試みでは、有効な着手と無効な着手を識別する能力の観点でネットワークを評価します。
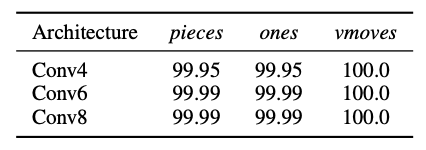
表Ⅳに、特定のネットワークのテストセットの精度を示します。
考慮されている全てのネットワークとエンコーディングにより、この指標は完璧なものに近く、vmoves を使用するネットワークはこの文脈においては全く間違えません。
これは、構成に関係なく、有効な着手と無効な着手を区別するのがとても簡単であり、その情報を vmoves で明示的に提供する必要が無いだけでなく、訓練処理の邪魔になる可能性があることを意味します。
したがって、以降の全ての実験では、pieces エンコーディングを使用することにします。
3) 正則化とバギングの影響
表Ⅴ: ドロップアウト,バッチ正則化,バギングが予測精度に及ぼす影響。pieces エンコーディングを使っています。
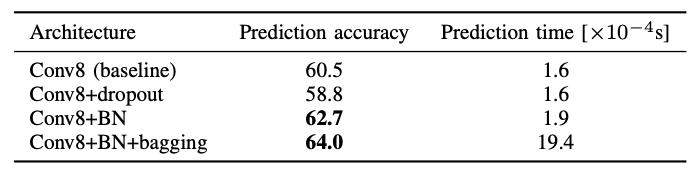
表Ⅴに、CNN の一般化パフォーマンスを改善する傾向が見られたいくつかの手法の影響を示しました。
ドロップアウトは、訓練データセットの個々のバッチに対してランダムにユニット(ここでは50%)を無効にします。
これにより、入力から出力への複数の代替経路を作ることを強制できます。
その結果、通常、ネットワークがより堅牢になり、特に入力データがもともと冗長である分野(数千ピクセルで構成される自然画像など)では、過学習を抑制できます。
ただし、オセロの盤面状態は事情が大きく異なります。入力が 64 個しかないため、着手を選択する時に全ての石がカウントされます。
つまり、オセロでは、実質的に入力値に冗長性がないのです。
表Ⅴが示すように、ドロップアウトは Conv8 ネットワークが盤面状態を完全にキャプチャすることを妨げ、予測精度に悪く働きます。
バッチ正則化の目的は、セットのバッチ全体で個々のネットワークユニットの出力を標準化することにより、内部共変量シフト[14]に対処することです。
これは、多くの文脈において有益であることが実証されています。
この場合、精度が 2 % 以上向上していることが裏付けられているため、この論文の残りでは、この構成をベースラインとします。
最後に、bootstrap aggregation (バギング)を使用して分類器の分散を減らすことを試みます。
訓練セットから bootstrap sampling されたデータで 10 個のネットワークを訓練し、対応する出力を平均して着手を決定します。
Conv8 + BN ネットワーク(表Ⅴ)に適用すると、バギングによってパフォーマンスが 64 % に向上します。
そのためには、訓練時間だけでなく予測時間も 10 倍に増加するという代償を支払う必要があります。
これは、他の対戦相手と対峙する、調査の後半で影響してきます。
4) スキップ接続のあるアーキテクチャ
最近の深層学習の研究では、数十のレイヤーを含むとても深いネットワークアーキテクチャが示され[37],[12]、これが画像分類の最先端になりました。
このようなネットワークの訓練は、レイヤー間の経路にショートカットを形成する skip connections を目的とした場合のみ可能です。通常、特定のレイヤーで学習した表現(特徴マップ)を、連続するレイヤーの 1 つで学習した表現に追加します。
これをネットワーク全体で複数回繰り返すと、訓練目標を達成するための新しい道を開きます。
その道とは、ネットワークが、 y(x) = H(x) のようなマッピング H を学習するのではなく、 y(x) = F(x) + x のように残差 x を学習するということです。
スキップ接続により、勾配が多くのレイヤーを介して変更されずに逆伝播する可能性があるため、勾配消失問題を緩和するのです。
表Ⅵは、いくつかのスキップ接続アーキテクチャの予測精度を示しています。
ResNet の N ネットワーク[12]は、n/2 個の残差ブロックで構成され、各ブロックは非線形層(ReLU アクティベーション)とそれに続く線形層、そして最初の層の入力を 2 番目の層の出力に追加するスキップ接続のショートカット で構成されます。
もともと画像分析用に設計された ResNet は、入力の次元数を減らすダウンサンプリングを実行しますが、非常に小さい 8×8 入力の場合はその必要が無いので、その機能を取り除いた変形版の ResNet-N-np を検討します。
予想通り、学習全体を通じて入力の次元を維持すると、小さいアーキテクチャ(ResNet-32)と大きいアーキテクチャ(ResNet-56)の精度が向上します。
レイヤーの出力の単純な追加は、それらが同じ次元である場合にのみ可能です。
それ以外の場合、ResNet アーキテクチャの作成者は、スキップ接続を線形マッピングとして実装することを提案しています。
表Ⅵの ResNet-N-np-p 構成はその機能を実装しており、予測がわずかに改善されています。
ResNet のスキップ接続は、それぞれが同じ残差ブロックの入力と出力に跨るため、1 次と見なすことができます。
DenseNets[13]では、レイヤーの各ペア間にスキップ接続が導入されているため、Iレイヤー(あるいは残差ブロック)のネットワークには、l(l-2)/2 個のスキップ接続があります。
我々は 2 つの DenseNet アーキテクチャを訓練しました。
小さい方のアーキテクチャ(DenseNet-40)は、このセクションで検討した他のネットワークと同等のパフォーマンスを発揮しました。大きい方(DenseNet-100)はそれらを大幅に上回り、ベースラインのパフォーマンスレベルにほぼ到達しました。
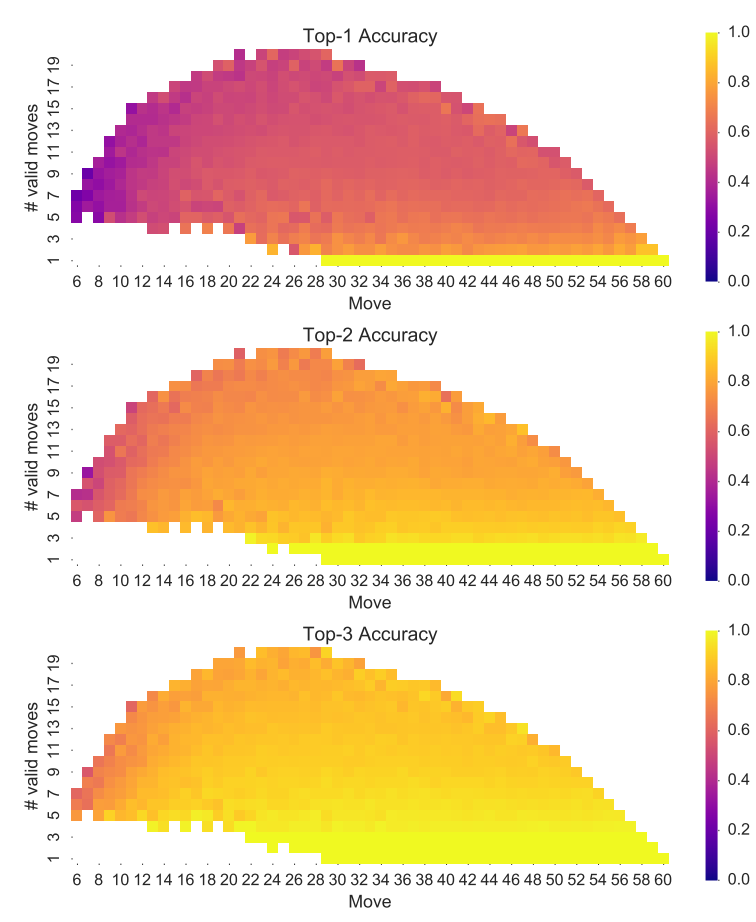
図Ⅲ: ゲームにおける着手回数と合法手の数に関する、トップ k の予測精度。
最後に、WideNet[43]と名付けられたアーキテクチャに関する最近の研究によると、残差ブロックの表現をより豊かにすることで、残差ネットワークのレイヤー数(要はパラメータ)を大幅に削減でき、精度を全く損なわないことが明らかになりました。
これは、ブロック内の畳み込み層を増やすか、特徴マップの数を増やすか、あるいはその両方によって実現できます。
このアーキテクチャの例は、残りブロック 3 つのスタックで構成され、各スタックは 6 つのブロックで構成されます。
各残差ブロックには、2 つの 3×3 畳み込み層が含まれます。
連続するスタックのレイヤーには、それぞれ 64, 128, 256 の特徴マップが備わっているため(k=4 の場合は[43]の表1を参照)、ネットワークは元の ResNet の 4 倍の幅になります。
表Ⅵの最後の行が示すように、この WideNet 構成は、ここで検討したスキップ接続アーキテクチャの中で最も優れています。
これは、処理の様々な段階で複数の特徴を集約することが、着手予測を成功させるために不可欠であることを示しています。
ただし、WideNet-40-4 は、クエリ実行が最も遅いネットワークの 1 つでもあります。
しかしながら、全体として、予想に反し、非常に深いスキップ接続ネットワークはいずれも Conv8 + BN ベースラインを上回っていませんでした。
5) 予測精度の分析
着手予測タスクは本質的に複数の手段に基づきます。上手くプレイするには、ゲーム序盤とゲーム終盤に発生する盤面状態について、ゲームの全過程に沿って正しい予測を行う必要があります。
それ故、ゲームの特定の段階でネットワークが上手く機能することがどれだけ難しいかを問うのは、興味深いことです。
ここで我々は、予測精度の観点からこの問いに答えます。
Ⅲで、ベースラインである Conv8 + BN の上位 k の予測精度を示しましたが、これは、ゲームにおける着手回数と特定局面での合法手数を考慮したものです。
初期配置で 4 つの石があるとすると、前者の数(ゲームにおける着手回数)は 5 から 60 まで変化します。ただし、5 番目の着手はオセロの対称性(ここでは考慮するものとします)の下では常に同じである(f5,d6,c4,e3 はどれも同じ)ため、6 から示すことにしました。
データポイントの色は、(WThor テストセットによる)正しい着手がネットワークによって示される上位 k の中にある確率を反映しています。
この図は、予測精度がゲーム全体でほぼ一貫していることを示しています。
ゲームの序盤時のみ、ネットワークの予測精度が低下します。これは、この序盤の Unique-S 訓練データが比較的少ないためです。(同一のものが多いのです)
トップ 1 とトップ 3 のグラフの違いによって、プレイに関して分かる他のことがあります。それは、勝利への代替経路が多くあること、そしてその選択には、プレイヤーの個人的な癖や好みが反映されており、序盤の一貫性の無いデータの大部分がそれであることです。
終盤が近づくにつれて 1 回の着手で盤面状態が大きく変わる可能性がある(この特徴は Othello が Othello という名である所以でもあります)ため、中盤以降(それまでの着手回数が多い局面)の推測が高品質であることは我々にとって励みとなります。
VI. プレイの強さ分析
我々は最終的には "強さ" に関心があるので、前のセクションで検討した予測精度はパフォーマンスの代用的な測定に過ぎません。
このセクションでは、予測子を他のプレイヤーと対戦させます。
A. 実験のセットアップ
我々が以前の調査[18]で収集および比較した、13 個の 1-ply プレイヤーたちを検討します。
それらは、お手製の設計や時間差学習、共進化などの様々な方法で訓練されており(cf. セクションⅡ)、重み付けされた石のカウンタと N タプルネットワークによってエンコードされた盤面評価関数を備えたプレイヤーです。
その一連の対戦相手に加えて、強力で高度に最適化されたオセロプログラムである、Edax の ver 4.3.24 との対戦も検証します。
Edax は、特定の ply (読みの深さ) でプレイすることが可能です。これを Edax-n と呼ぶことにします。
我々の着手予測子は、14 の対戦相手(Edax を含む)と同様に全て決定論的であるため、勝率の確固たる推定値を得る目的で我々は以下の手法を用います。
初期盤面から始まる単一のゲームをプレイするのではなく、我々は Runarsson と Lucas によって準備された 1000 個の 6-ply オープニング[30]を使用することにします。
そうやっていくつかの初期状態から始めることとし、2 つのゲームをプレイして、プレイヤーの手番(色)を切り替えます。
1 つのゲームについて、勝ちで 1, 引分で 0.5, 負けで 0 ポイントを得られることとします。
我々は、勝率、すなわち 2000 ゲーム(1000 個 6-ply オープニングの両手番分)で獲得できるポイントを示したいと思います。
B. プレイの強さ評価
セクションⅤから、5 つの最良な予測子を代表として選び、13 人の対戦相手全てと Edax-1 と対戦しました。
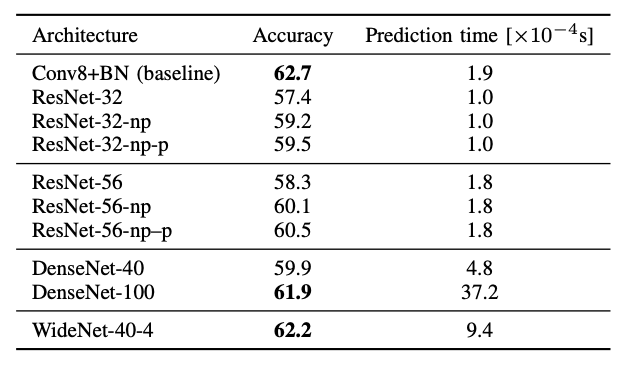
表Ⅶ: 1-ply に対する最高のパフォーマンスを発揮する最良の着手予測子の勝率。CoCMAES は 13 の対戦相手に含まれていますが、Edax-1 は含まれていない点に注意して下さい。
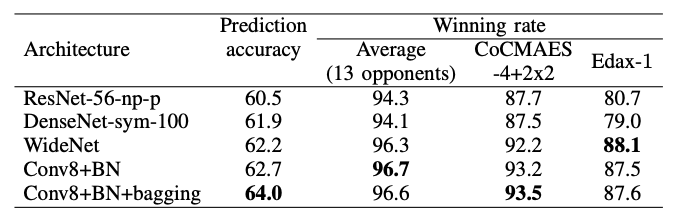
表Ⅶは、13 のプレイヤーに対する平均勝率と、[18] で最高であることが証明された CoCMAES-4+2×2 と、Edax-1 に対する勝率を個別に示しています。
全てのネットワークは、既存の 1-ply 先読みプレイヤーよりも大幅に強力であり、それらに対して約 90 % の勝率を達成しています。
着手予測子は先読みを行わないため、本質的には 0-ply 戦略なことを考えると、これは興味深い結果だと言えます。
Conv8+BN は最高の平均勝率を達成しました。ただし、CoCMAES-4+2×2 と対戦する場合は Conv8+BN+バギング よりも僅かに劣ります。Edax-1 と対戦する場合は WideNet よりも僅かに劣ります。
この全体的なパフォーマンスは、その高い予測精度を裏付けています。
表Ⅶで観測された予測精度と勝率の間のほぼ単調な関係性を見ると、そのような傾向が一般的なものであるかどうかを問いたくなります。
図Ⅳ: ネットワークの着手予測精度に関する、13 の対戦相手全てのプレイヤー(赤い点)および Edax-1 (青い三角形) に対する勝率。
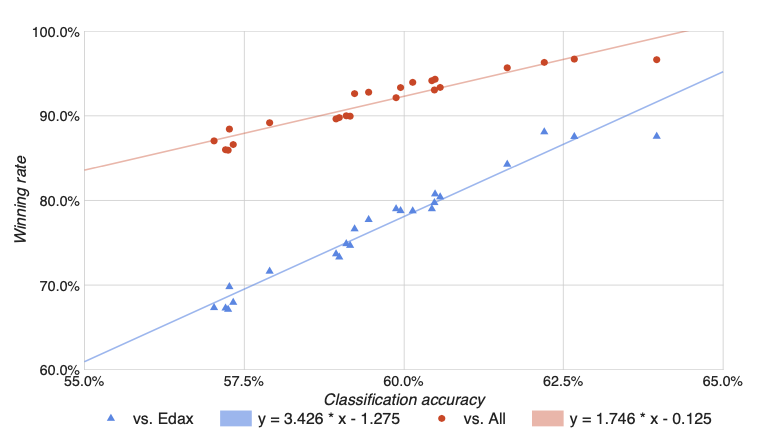
図Ⅳでは、各プレイヤーのモデルや Edax-1 と直面した時について、この論文で評価した全てのネットワークについて後者を前者に対してプロットしています。
グラフは、非常に強い線形従属関係を示しています。(決定係数は、それぞれ r2=0.997、r2=0.999)
線形モデルの適合は、考慮された予測精度の範囲(57~64%)において、予測精度が 13 のプレイヤーに対して 1.7 % ポイント、Edax-1 に対して 3.4 % ポイントがもたらされることを示唆しています。
Conv8+BN+バギング(右端の2つのデータポイント)に示されているように、明らかに、この傾向が全体で維持されているとは言えません。
それは外れ値かもしれませんが、63 % という数値が、予測精度の更なる向上が勝率にあまり寄与しない閾値であることを示唆している可能性もあります。
C. プレイ強さに対するデータ増強の効果
セクションV-B1 で重複を取り除き、オセロの対称性を利用して拡張された訓練セット Unique-S が、最高の着手予測精度をもたらすことが発見できました。
ただし、予測精度は、私たちが本当に興味のある "強さ" の代用的な指標に過ぎません。
したがって、同様の主張がプレイの強さに当てはまるかどうかは明らかで無いため、このセクションでは、セクションV-B の基本的な畳み込み予測子を、一連のプレイヤーと対戦させます。
その他の設定は前のセクションと同じです。
表Ⅷ: 様々なデータセットで訓練された基本的なニューラル予測子の、13 のプレイヤーに対する勝率

表Ⅷに示されている勝率は、表Ⅱに示されている予測精度で裏付けられます。
重複除去と、増強の両方がプレイの強さに大きなプラスの効果をもたらしています。
この相関関係は、少なくとも一定の間隔で、着手予測精度が "強さ" の信頼できる因子であることを改めて示していると言えます。(cf. 図4)
D. ゲームツリー検索との対戦
セクションⅥ-Bで、0-ply のニューラル着手予測子が 1-ply の対戦相手よりも優れており、大幅な差があることを明らかにしました。(同点の 50 % に対して、約 90 %)
対戦相手に深いゲームツリー検索を許した時に、そのマージンがどのように減少するかを見るのは興味深いことです。
表Ⅸ: Conv8+BN の Edax-n に対するパフォーマンス

それを調査するために、Conv8+BN を Edax-n (n ∈ [2, 5]) と対戦させ、結果を表Ⅸに集めました。
驚くべきことに、Edax に 2-ply の先読みを許した場合、予測子は優位性を維持しますが、その勝利のオッズは今のところおよそ 6 : 4 に過ぎません。
読みの深さを 3 から開始すると、Conv8+BN は勝ちよりも負けの可能性が高く、5-ply の読みの深さを許すと、勝率は 1 : 9 にまで下がります。
オセロの平均分岐係数が 10 であることを考えると、これは依然として印象的です。
読みの深さが 5 の場合、Edax の決定は、それぞれが数万の盤面状態に基づいていますが、一方でニューラル予測子は 1 つだけで非常にうまく機能しているのです。
読みの深さは、Edax が着手するのに使う平均時間に影響します。これは、表Ⅸでも示してあります。
Edax は高度に最適化されているため、読みの深さ 3 で Conv8 CNN の時間(1.9×1.0-4s)に匹敵する速度で着手できます。
より深い検索を Edax でしようとすると、もちろんより長い時間がかかります。
しかしながら、一方で、ニューラル予測子について報告された時間は、GPU コンピューティングの一般的な効率化手段である 256 の盤面状態のバッチで評価されています。
単一の盤面状態の着手を予測するように求められた場合、CNN は 5~20 倍遅くなります。
表Ⅸには、Original データセットに対する Edax の予測精度も含まれています。
これを見るに、読みの深さに応じて精度が高くなっていることが分かります。ただし、読みの深さを 4 から 5 に増やしても、Conv8+BN に対する一致度が増加するだけで、精度は向上しません。
また、Edax の予測精度 (n=5 で 99 %)は、Conv8+BN によって示される 64 % よりも大幅に低くなっています。
したがって、Edax は、CNN が模倣しようとする人間のプレイヤーとは異なる方法でプレイしているようです。
E. ゲームステージの分析
我々の 0-ply 着手予測子のパフォーマンスが印象的であったのと同程度に、以前の実験は高い勝率のためにはより深い先読みが不可欠なことを示しています。
我々の最後の実験では、着手予測子をゲームツリー検索で補完する際に、どのゲームステージが最も効果的か(そして逆にどのゲームステージがニューラル予測子に最も問題があるか)を求めることにします。
この目的のために、手数の間隔によってゲームを 4 つのステージ、[1,15], [16,30], [31,45], [46,60] に分割します。
各ステージで、Edax-5 を使用するハイブリッド戦略を設計し、残りのステージで Conv8+BN ポリシーを使用して意思決定を行います。
我々は、これらのハイブリッド戦略を Edax-1 ~ Edax-5 と対戦させます。
図Ⅴ: ゲームの特定ステージにおける、Edax-5 vs ハイブリット化した Conv8+BN の勝率推移。勝率は、Edax-1 ~ Edax-5 に対して独立に評価されています。
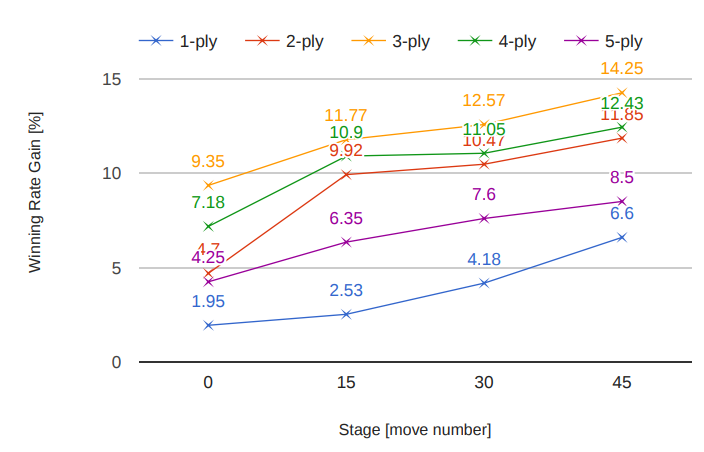
図Ⅴに要約された結果は、どのステージにおいても Edax に着手させることで、ハイブリッド戦略のパフォーマンスが向上することを示しています。
Gain は n=3 で最大です。セクションVI-D で示したように、n が小さい場合、純粋な Conv8+BN で比較的簡単に Edax を打ち負かすことが既に可能なため、単一のゲームステージで Edax-5 を使用しても、勝率はさほど向上しません。
逆に n > 3 の場合、対戦相手の Edax-n は非常に強くなるため、勝率を上げることが困難になります。
グラフは、対戦相手の読みの深さに関係なく、ゲームの後半で Edax に着手させることが勝率に繋がることも示しています。
これは、ゲームの分岐数の性質によるものと思われます。これにより、CNN のパターン認識能力は、ゲームの終盤での成功との関連性が低くなります。
オセロは最大 60 の着手が行われることを考えると、終盤で読みの深さ 5 による探索を行うことで、Edax はしばしば終局図に辿り着き、潜在的な着手の堅牢な評価を下すことができます。
大事なことを言い忘れましたが、WThor から得た着手の一部は最適でない可能性があるため、ネットワークを "だましている" 可能性はあります。
Ⅶ. 議論
精度が 63 % 近くある深い CNN ベースの着手予測子は、同じデータセットで 53 % しか達成できなかった N タプルベースの順序学習[30]よりも遥かに優れていることが分かりました。
我々の Conv8+BN は、それに対して 93.9 % の勝率を収めました。これまでで最強の 1-ply プレイヤーである CoCMAES プレイヤー[18]に対しても、同様の勝率 93.2 % を得ることができました。(cf. 表Ⅶ)
オセロの分岐係数は比較的に小さく、盤面サイズが小さいにも関わらず、CNN は最高の着手予測子であることが証明され、何百万もの人間の着手により表現される専門知識を効率的に学習することができました。
離散値の小さい盤面状態が、自然の画像とは間違いなく大きく異なることを考えると、この結果は印象的なものです。
畳み込み演算を使用する主な動機は並進不変性であるため、並進不変性がほとんどないボードゲームにおいて CNN が非常にうまく機能したのは興味がそそることです。
これは、オセロで観測される特定のパターンがある程度並進不変であることを示唆しています。
また、少なくとも、非線形性と絡み合ったいくつかの畳み込み層のスタックによって実装される "高次な畳み込み" を使用して検出できることを示唆しています。
アプローチの限界について述べておくと、我々は、スキップ接続のあるより深いネットワークを使用して Conv8+BN ネットワークでの結果を改善することはできませんでした。
これは、高次元の画像データで機能するものが、オセロなどの低次元の問題でも常に成功するとは限らないことを示唆しています。
訓練に関して得られた興味深い観測は、大規模なネットワークがデータにほとんど適用しないことです。
訓練セットの分類精度は、通常、テストセットの精度の 1 %以内です。これは、ここで検討したネットワークでは、訓練データを完全に記憶できないことを示しています。
したがって、我々は、それらのアーキテクチャを改善する余地がまだあると結論づけます。
とりわけ、これは畳み込み処理固有の制限である兆候な可能性があり、サイズの制限された RF は、盤面全体で発生する任意の複雑な組み合わせパターンをキャプチャするには不十分な可能性があります。
フォローアップのステップは、その制限を受けない、完全に接続されたネットワークを検討することです。
ただし、訓練にかかるコストも遥かに高く、過学習する傾向にあります。これに関連して、最大 3 つの隠れ層を持つ完全に接続されたネットワークに関する興味深い研究が[3]で行われています。
Ⅷ. 結論
我々の研究は、深層学習がオセロエージェントを訓練するために有用な手法であるという証拠を示しました。
ゲームのルールや戦略に関する明確な知識、広範なゲームツリーの検索、個々の盤面状態や着手の先読みの明示的な比較などを必要としません。
それよりも、盤面状態から観測されるパターンと目的の着手との関連を学習することで、高レベルなプレイを実現したのです。
したがって、ある程度は、訓練されたニューラル着手予測子がオセロというドメインの専門知識を具現化すると主張して良いかもしれません。
これは、主にアルゴリズムの効率が強さの多くを占めているゲームツリー検索技術では、カバーすることが難しいところです。
一方、ここで提案されている教師あり学習アプローチは、例えば進化的学習や強化学習の方法と同じ意味で、"専門知識と関連が無い"などと言い切ることはもちろんできません。
今回で言えば、訓練に使用されるエキスパートたちのゲームに本質的な専門知識が隠されているわけです。
CNN の力は、その知識を抽出して、訓練データにとどまらずに一般化されたシステムとして表現できるところにあります。
これまで、オセロでエキスパートレベルのプレイを達成するのに十分な方法は他にありませんでした。
CNN の最高のパフォーマンスを考慮すると、この作業はいくつかの方向に展開する価値があるかもしれません。
セクションⅦで言及した、完全に接続されたレイヤーに頼ったネットワークを構築することは、その 1 つです。
Logistello[7]と Edax は、ゲームの各ステージで異なる評価関数を使用(cf. セクションⅥ-E)しますが、そのような "ゲームのコーナーケースに基づく因子の分解" も CNN エージェントのパフォーマンス向上に寄与する可能性があります。
他には、確かな拡張として、着手するプレイヤーに関する情報を追加することが考えられます。これは、オセロが非対称ゲームであることを考えると有益でしょう。
最後になりますが、ここで証明された、畳み込まれた特徴の有用性を考えると、着手予測子の教師あり学習以外の文脈でそれらの特徴を検証することは興味深いと思います。例えば、強化学習法で訓練された状態あるいは評価関数として。
謝辞
P. Liskowskiは、ポーランドの国立科学センターから資金提供(2014/15/N/ST6/04572)を受け、感謝しています。
W. Jaskowskiは、Ministry of Science と "MobilityPlus" からの資金提供(1296/MOB/IV/2015/0)を受け、感謝しています。
K. Krawiec は、ポーランドの国立科学センターの助成金サポート(2014/15/B/ST6/05205)を受けました。
以上翻訳。