$$\def\mA{\mathbf{A}} \def\mB{\mathbf{B}} \def\mC{\mathbf{C}} \def\mD{\mathbf{D}} \def\mE{\mathbf{E}} \def\mF{\mathbf{F}} \def\mG{\mathbf{G}} \def\mH{\mathbf{H}} \def\mI{\mathbf{I}} \def\mJ{\mathbf{J}} \def\mK{\mathbf{K}} \def\mL{\mathbf{L}} \def\mM{\mathbf{M}} \def\mN{\mathbf{N}} \def\mO{\mathbf{O}} \def\mP{\mathbf{P}} \def\mQ{\mathbf{Q}} \def\mR{\mathbf{R}} \def\mS{\mathbf{S}} \def\mT{\mathbf{T}} \def\mU{\mathbf{U}} \def\mV{\mathbf{V}} \def\mW{\mathbf{W}} \def\mX{\mathbf{X}} \def\mY{\mathbf{Y}} \def\mZ{\mathbf{Z}} \def\va{\mathbf{a}} \def\vb{\mathbf{b}} \def\vc{\mathbf{c}} \def\vd{\mathbf{d}} \def\ve{\mathbf{e}} \def\vf{\mathbf{f}} \def\vg{\mathbf{g}} \def\vh{\mathbf{h}} \def\vi{\mathbf{i}} \def\vj{\mathbf{j}} \def\vk{\mathbf{k}} \def\vl{\mathbf{l}} \def\vm{\mathbf{m}} \def\vn{\mathbf{n}} \def\vo{\mathbf{o}} \def\vp{\mathbf{p}} \def\vq{\mathbf{q}} \def\vr{\mathbf{r}} \def\vs{\mathbf{s}} \def\vt{\mathbf{t}} \def\vu{\mathbf{u}} \def\vv{\mathbf{v}} \def\vw{\mathbf{w}} \def\vx{\mathbf{x}} \def\vy{\mathbf{y}} \def\vz{\mathbf{z}} \def\veps{\boldsymbol{\epsilon}} \def\vnu{\boldsymbol{\nu}} \def \vmu{\boldsymbol{\mu}} \def\mSigma{\boldsymbol{\Sigma}} $$
はじめに
前回はKalman filter (KF)の解説を行いました。Kalman filterでは状態遷移モデル・観測モデルに強い制約があったため、使える場面が限られていました。この記事では、この制約を取り除いたExtended Kalman filter (EKF) と、求めたい事後分布をサンプルの集合で表現するPaticle filter (PF) について説明していきます。
参考文献
[1] Probabilistic robotics 3章・4章
[2] パター認識と機械学習 下 11章・13章
数式表記
- $x$(小文字+イタリック)$\rightarrow\ $スカラー
- $ \vx$(小文字+太字)$\rightarrow\ $列ベクトル
- $\mA$(大文字+太字)$\rightarrow\ $行列
- $\approx\ \rightarrow\ $近似
- $\vx \sim p(\vx) \rightarrow \ $確率変数$\vx$が分布$p(\vx)$に従う
状態空間モデル
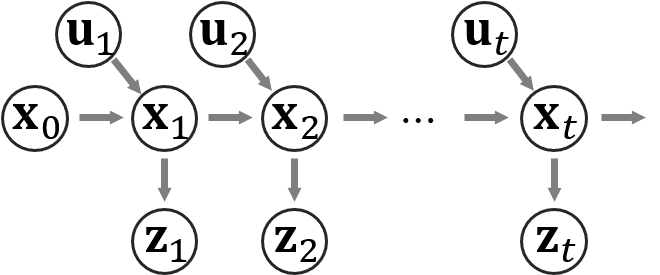
復習のため、前回と同じ状態空間モデルの図を示しておきます。$\vx_t$は例えば時刻$t$でのロボットの位置などの状態を表し、$\vz_t$は時刻$t$でのセンサの観測値を表します。$\vu_t$は例えば$\vx_{t-1}$から$\vx_t$にロボットの状態が変化する際にコントローラなどから与えた指示や、オドメトリ(タイヤの回転数などから計算した移動量)などの情報を表します。この状態空間モデルは変数間の関係を表しており、$\vx_{t-1} \rightarrow \vx_t$の関係を状態遷移モデル、$\vx_t \rightarrow \vz_t$の関係を観測モデルと呼びます。前回のKFの場合には、2つのモデルの設計の際に強い制約があり、以下の式で関係が表されないといけませんでした。
\begin{align}
\vx_{t} &= \mA \vx_{t-1} + \vb + \veps \\
\vz_{t} &= \mC \vx_{t} + \vd + \vnu
\end{align}
ここで、$\veps \sim \mathcal{N}(\mathbf{0}, \mQ)$、$\vnu \sim \mathcal{N}(\mathbf{0}, \mR)$はガウス分布に従うノイズを表します。EKFやPFではこの制約は必要ないため、状態遷移モデルと観測モデルを以下で表します。
\begin{align}
\vx_{t} &= \vf(\vx_{t-1}, \vu_t) + \veps \\
\vz_{t} &= \vg(\vx_{t}) + \vnu
\end{align}
$\vf(), \vg()$はそれぞれ$\vx$と$\vz$と同じ次元の値を返す任意の関数です。
Extended Kalman filter
KFの場合と同様に$p(\vx_{t-1}|\vu_{1:t-1}, \vz_{1:t-1}) = \mathcal{N}(\vx_{t-1}|\vmu_{t-1}, \mSigma_{t-1})$まで求まっているとして、$p(\vx_{t}|\vu_{1:t}, \vz_{1:t})$を計算することがEKFの目標となります。KFの場合と同様にまず以下のように$p(\vx_{t}|\vu_{1:t}, \vz_{1:t})$を分解していきます。
\begin{align}
p(\vx_t | \vu_{1:t}, \vz_{1:t}) &= \frac{p(\vz_t | \vx_t, \vu_{1:t}, \vz_{1:t-1}) p(\vx_t | \vu_{1:t}, \vz_{1:t-1})}{p(\vz_t | \vu_{1:t}, \vz_{1:t-1})} \\
&\propto p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1})
\end{align}
状態遷移モデルや観測モデルが線形でない場合に問題となるのは、$p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$の計算と、$p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$を$\vx_t$の2次式になるように整理する部分です。
EKFのアイデアは非常に単純で、$\vf(\vx_{t-1}, \vu_t)$や$\vg(\vx_{t})$を$\mA \vx + \vb$の形に近似することによってKFの場合と同様に扱えるようにするだけです。そのため、まず$\vf(\vx_{t-1}, \vu_t)$を平均$\vmu_{t-1}$の周りでテイラーの1次近似を用います。
\begin{align}
\vx_t = \vf(\vx_{t-1}, \vu_t) + \veps
&\approx
\vf(\vmu_{t-1}, \vu_t) + \left.\frac{\partial \vf}{\partial \vx}\right|_{\vx=\vmu_{t-1}} (\vx_{t-1} - \vmu_{t-1}) + \veps \\
&= \mF_t \vx_{t-1} + \left(\vf(\vmu_{t-1}, \vu_t) - \mF_t \vmu_{t-1} \right) + \veps
\end{align}
2行目では$\mF_t = \left.\frac{\partial \vf}{\partial \vx}\right|_{\vx=\vmu_{t-1}}$としています。$\frac{\partial \vf}{\partial \vx}$は ($\vx$の次元)$\times$($\vx$の次元) の行列であり、その$(i, j)$成分は$\vf(\vx, \vu)$の第$i$成分を$\vx$の第$j$成分で偏微分した値になっています。この式の意味は図を見れば分かるかと思います。

これによって、KFの場合と同様にして、$p(\vx_{t-1}|\vu_{1:t-1}, \vz_{1:t-1}) = \mathcal{N}(\vx_{t-1}|\vmu_{t-1}, \mSigma_{t-1})$であることから、以下のように$p(\vx_{t}|\vu_{1:t-1}, \vz_{1:t-1})$が計算できます。
\begin{align}
p(\vx_t | \vu_{1:t}, \vz_{1:t-1}) &\approx \mathcal{N}(\vx_{t} | \vf(\vmu_{t-1}, \vu_t), \mF_t \mSigma_{t-1} \mF_t^T + \mQ) \\
&= \mathcal{N}(\vx_{t} | \tilde{\vmu}_t, \tilde{\mSigma}_{t} )
\end{align}
$\vg(\vx)$については、今得られた$\tilde{\vmu}_t$の周りで同様に1次近似します。
\begin{align}
\vz_t = \vg(\vx_t) + \vnu
&\approx
\vg(\tilde{\vmu}_{t}) + \left.\frac{\partial \vg}{\partial \vx}\right|_{\vx=\tilde{\vmu}_{t}} (\vx_{t} - \tilde{\vmu}_{t}) + \vnu \\
&= \mG_t \vx_t + ( \vg(\tilde{\vmu}_{t}) - \mG_t \tilde{\vmu}_{t}) + \vnu
\end{align}
したがって、$p(\vz_t | \vx_t)$は以下のように書くことができます。
\begin{align}
p(\vz_t | \vx_t) &\approx \mathcal{N}(\vz_t | \mG_t \vx_t + ( \vg(\tilde{\vmu}_{t}) - \mG_t \tilde{\vmu}_{t}), \mR)
\end{align}
あとは、KFの場合と同様に$p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$から$\vx_t$の2次の項、1次の項を取り出して、平均と分散を計算するだけです。
まとめると、以下がEFKの更新式になります。
\begin{align}
\tilde{\vmu}_{t} &= \vf(\vmu_{t-1}, \vu_t) \\
\tilde{\mSigma}_{t} &= \mF_t \mSigma_{t-1} \mF_t^T + \mQ \\ \\
\mK_t &= \tilde{\mSigma}_t \mG_t^T (\mG_t \tilde{\mSigma}_t \mG_t^T + \mR)^{-1} \\
\vmu_t &= \tilde{\vmu}_t + \mK_t(\vz_t - \vg(\tilde{\vmu}_{t} ) ) \\
\mSigma_t &= (\mI - \mK_t \mG_t) \tilde{\mSigma}_t
\end{align}
以下のKFの更新式と比較するとほとんど同じになっていることがわかるかと思います。KFにおいて$\mA \vx_{t-1} + \vb$に$\vx_{t-1} = \vmu_{t-1}$を代入しているのと同様に、$\mF_t \vx_{t-1} + (\vf(\vmu_{t-1}, \vu_t) - \mF_t \vmu_{t-1})$に$\vx_{t-1} = \vmu_{t-1}$を代入したのが1行目であり、$\mC \vx_t + \vd$に$\vx_t = \tilde{\vmu}_t$を代入しているのと同様に、$\mG_t \vx_t + ( \vg(\tilde{\vmu}_{t}) - \mG_t \tilde{\vmu}_{t})$に$\vx_t = \tilde{\vmu}_t$を代入したのが4行目になっています。
\begin{align}
\tilde{\vmu}_{t} &= \mA \vmu_{t-1} + \vb \\
\tilde{\mSigma}_{t} &= \mA \mSigma_{t-1} \mA^T + \mQ \\
\mK_t &= \tilde{\mSigma}_t \mC^T (\mC \tilde{\mSigma}_t \mC^T + \mR)^{-1} \\
\vmu_t &= \tilde{\vmu}_t + \mK_t(\vz_t - (\mC \tilde{\vmu}_t + \vd)) \\
\mSigma_t &= (\mI - \mK_t \mC) \tilde{\mSigma}_t
\end{align}
Particle filter (PF)
PFの説明は[2]を参照しています。PFの考え方はKFやEKFと大きく異なり、$p(\vx_t|\vu_{1:t}, \vz_{1:t})$をガウス分布で表現するのではなく、サンプルの集合を用いて近似します。どういうことかと言うと、$p(\vx_t|\vu_{1:t}, \vz_{1:t})$の値の大きさをサンプルの数で表現する、つまり値が大きいところ付近にはサンプルが多く分布し、値が小さい所にはサンプルがほとんど分布しないようなサンプルの集合で確率分布を表現するということです。
KFやEKFでは$p(\vx_t|\vu_{1:t}, \vz_{1:t})$がガウス分布で表されるため、例えばロボット位置の推定問題ではガウス分布の平均パラメータが推定値として使われることがあります。PFの場合には同じようにはできませんが、代わりに、$\vx_t$についての関数$h(\vx_t)$の期待値をモンテカルロ法により近似することができます。
\begin{align}
\mathbb{E}_{p(\vx_t | \vu_{1:t}, \vz_{1:t})}[h(\vx_t)] &= \int h(\vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t}) d \vx_t \\
&\approx \frac{1}{M} \sum_{m=1}^M h(\vx_t^{(m)})
\end{align}
ここで、$\vx_t^{(m)}$は$p(\vx_t^{(m)} | \vu_{1:t}, \vz_{1:t})$からの$m$番目のサンプルを表します。状態$\vx_t$自体の期待値が欲しいならば、$h(\vx_t) = \vx_t$と置けば計算できます。
ではどのように$p(\vx_t|\vu_{1:t}, \vz_{1:t})$からサンプルを得るのかということですが、非線形な状態遷移モデルや観測モデルを考えているために$p(\vx_t|\vu_{1:t}, \vz_{1:t})$を解析的に計算できないというのが問題です。そのためPFでは Sampling Importance Resampling (SIR)というテクニックを用いてサンプリングを行います。
SIRとは、ある分布$p(\vx)$からのサンプリングをしたいけれど、それが困難である場合に、サンプリングが容易な他の分布$q(\vx)$からSamplingを行い、各サンプルの重み(Importance)を計算して、その重みに基づいてサンプル集合からもう一度サンプリング(Resampling)を行うことで、$p(\vx)$から擬似的にサンプリングする手法です。あるサンプル$\vx^{(m)}$の重み$w^{(m)}$は$p(\vx^{(m)})/q(\vx^{(m)})$によって計算されます。
今は$p(\vx_t | \vu_{1:t}, \vz_{1:t})$からのサンプリングを行いたいのですが、それができないので代わりに$p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$からのサンプリングを行います。すると重み$w^{(m)}$は以下のように計算されます。
\begin{align}
\frac{1}{M} \frac{p(\vx_t^{(m)} | \vu_{1:t}, \vz_{1:t})}{p(\vx_t^{(m)} | \vu_{1:t}, \vz_{1:t-1})}
&= \frac{p(\vz_t | \vx_t^{(m)}) p(\vx_t^{(m)} | \vu_{1:t}, \vz_{1:t-1})}{Mp(\vx_t^{(m)} | \vu_{1:t}, \vz_{1:t-1}) p(\vz_t|\vu_{1:t}, \vz_{1:t})} \\
&= \frac{p(\vz_t | \vx_t^{(m)})}{M \int p(\vz_t | \vx_t) p(\vx_t | \vu_{1:t}, \vz_{1:t-1}) d\vx_t} \\
&\approx \frac{p(\vz_t | \vx_t^{(m)})}{\sum_{m'=1}^M p(\vz_t | \vx_t^{(m')}) } = w^{(m)} \\
\end{align}
ここで、$M$はサンプルの総数を表し、$1/M$は$\{w^{(m)}\}$を全ての$m$について足し合わせた時に1にするための正規化係数です。これで各サンプルの重みが計算できたので、あとは$M$個のサンプルからこの重みに基づいてサンプリングし直すだけです。このサンプル集合を用いると、$p(\vx_t^{(m)} | \vu_{1:t}, \vz_{1:t})$は以下のように近似することができます。
\begin{align}
p(\vx_t | \vu_{1:t}, \vz_{1:t}) \approx \frac{1}{M} \sum_{m=1}^M \delta(\vx_t - \vx_t^{(m)})
\end{align}
ここで、$\delta(\vx)$はディラックのデルタ関数(wiki)を表します。簡単に説明すると、$\vx=0$の時にのみ無限大の大きさを持つような関数で、積分すると1になるという性質を持ちます。これはつまりサンプル点が存在する位置でのみ値を持つような確率分布になっています。
残りの問題は$p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$からどのようにサンプリングをするかということだけです。$p(\vx_{t-1} | \vu_{1:t-1}, \vz_{1:t-1})$がディラックのデルタ関数の和で近似されているとすると、$p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$は以下のように書き直すことができます。
\begin{align}
p(\vx_t | \vu_{1:t}, \vz_{1:t-1}) &= \int p(\vx_t | \vx_{t-1}, \vu_t) p(\vx_{t-1} | \vu_{1:t-1}, \vz_{1:t-1}) d\vx_{t-1} \\
&\approx \int p(\vx_t | \vx_{t-1}, \vu_t) \frac{1}{M} \sum_{m=1}^M \delta(\vx_{t-1} - \vx_{t-1}^{(m)}) d\vx_{t-1} \\
&= \frac{1}{M} \sum_{m=1}^M p(\vx_t | \vx_m^{(t-1)}, \vu_t) \\
&= \sum_{m=1}^M \frac{1}{M} \mathcal{N}(\vx_t | \vf(\vx_m^{(t-1)}, \vu_t), \mQ)
\end{align}
これはクラス数$M$で、各クラスの重みが全て$1/M$である混合ガウス分布になっています。混合ガウス分布からのサンプリングは、まずクラスをサンプリングして、そのクラスのガウス分布からサンプリングすればよいです(サンプルしたクラスは無視)。$p(\vx_t | \vu_{1:t}, \vz_{1:t-1})$からサンプリングする場合、各クラスの重みは同じなので、$M$回サンプルして各クラスが1回ずつ得られたと仮定すると、各ガウス分布から1つサンプリングすればよいということになります。これで$p(\vx_{t} | \vu_{1:t}, \vz_{1:t-1})$ からのサンプリングができるようになりました。以上をまとめるとPFは以下のようなアルゴリズムになります。
$p(\vx_{t-1} | \vu_{1:t-1}, \vz_{1:t-1})$に従うサンプル集合$\{ \vx_{t-1}^{(m)} \}$が得られていると仮定し、以下の1~3を新しい$\vu_t, \vz_t$が得られるたびに繰り返す
- 各サンプル$\vx_{t-1}^{(m)}$について、$ \mathcal{N}(\vx_t | \vf(\vx_{t-1}^{(m)}, \vu_t), \mQ)$ から$\vx_t^{(m)}$をサンプリング
- $\vx_t^{(m)}$の重み $w^{(m)} = p(\vz_t | \vx_t^{(m)})/\sum_{m'=1}^M p(\vz_t | \vx_t^{(m')})$ を計算
- サンプル集合$\{ \vx_{t}^{(m)} \}$から重み$\{ w^{(m)} \}$に基づいて$M$個サンプリングすると、このサンプル集合は$p(\vx_{t}^{(m)} | \vu_{1:t}, \vz_{1:t})$ からのサンプルになっている
まとめ
この記事では、前回紹介したKalman filterでは扱えなかった非線形な状態遷移モデル、観測モデルに対応するための手法としてExtended Kalman filterと Particle filterについて紹介しました。次の記事では、これらの手法を用いてSLAMの問題をどう扱うかについて説明していきます。