#初めに
本記事はJDLAのE資格の認定プログラム「ラビット・チャレンジ」における深層学習day3のレポート記事です。この記事では以下の内容について、そのモデルの概念から確認し、数式・実装を含めてまとめていきます。
- 再帰型ニューラルネットワークの概念
- LSTM(Long Short Term Memory)
- GRU
- 双方向RNN
- Seq2Seq
- Word2Vec
- Attention Mechanism
#再帰型ニューラルネットワークの概念
##Recurrent Neural Network(RNN)
再帰型ニューラルネットワーク(Recurrent Neural Network:RNN)は、時系列データの扱いを得意とするニューラルネットワークです。時系列データとは、ある要素が順番に
$$
x_{1}, x_{2}, x_{3}, \ldots, x_{T}
$$
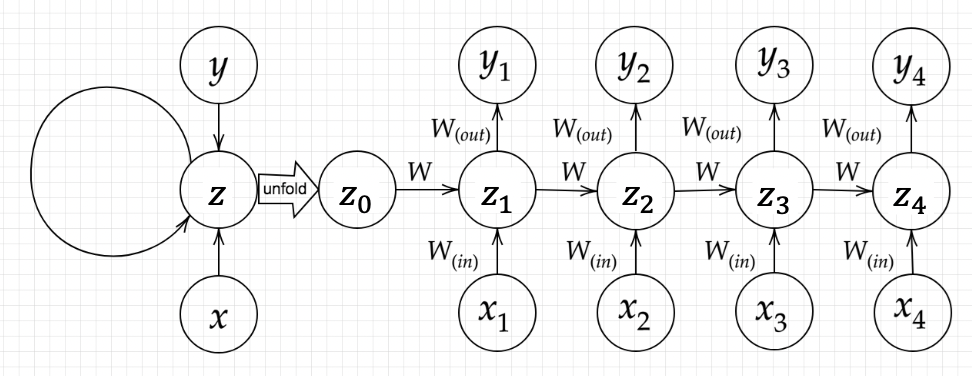
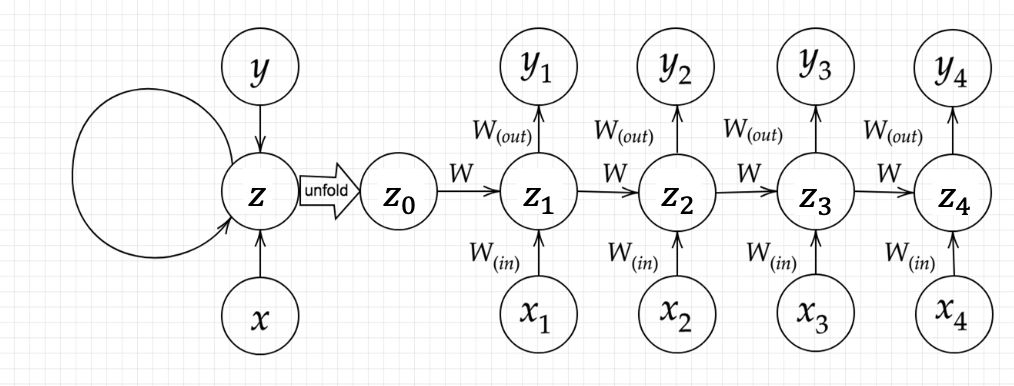
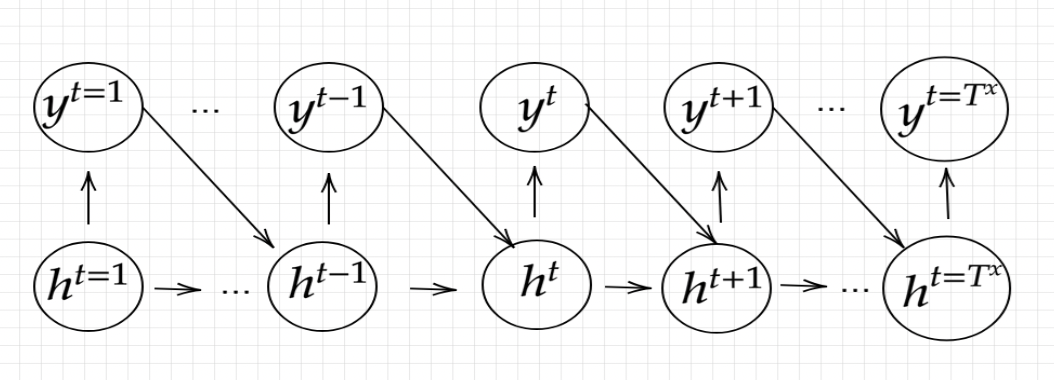
のように並んでいるデータのことを言います。このデータの添え字は通常tで表されますが、このtはデータの種類によって若干意味合いが異なります。時系列データの代表例として音声の波形、動画、文章(単語列)などがありますが、音声の波形なら一定の時間間隔(数ms)でのサンプル時間になりますし、文章なら単語を前から並べたときの番号になります。RNNの構造は下図のようになります。
ラビットチャレンジ講義資料
順伝播の式
\begin{gathered}
u^{t}=W_{(i n)} x^{t}+W z^{t-1}+b \\
z^{t}=f\left(W_{(i n)} x^{t}+W z^{t-1}+b\right) \\
v^{t}=W_{(o u t)} z^{t}+c \\
y^{t}=g\left(W_{(o u t)} z^{t}+c\right)
\end{gathered}
RNNの特徴
通常のニューラルネットワークでは、ある層の出力は、次の層の入力に利用されるのみです。しかしRNNでは、ある層の出力は、次の層の入力として利用されるだけでなく、一般的なニューラルネットワークの最後の層のような出力としても利用されます。また、各層の入力として、前の層の入力のみではなく、時系列のデータポイントも入力とします。このように、ニューラルネットワークの出力を別のネットワークの入力として利用するような再帰的構造を持ったニューラルネットワークのことをRecursive Neural Networkと呼びます。Recursive Neural Networkの中でも、隠れ層同士の結合が時系列に沿って直線的であり、かつその隠れ層が同一構造のものであるような場合を「RNN」といいます。RNNでは、再帰的に出現する同一のネットワーク構造のことをセル(cell)と呼びます。
##Backpropagation Through Time(BPTT)
基本的には、全損失Lを時間t=1からt=Tまでのすべての損失関数の総和であると考えます。
$$
L=\sum_{t=1}^{T} L^{(t)}
$$
時間tまでの損失は、それ以前のすべての時間刻みの隠れユニットに依存するため、勾配は次のように計算されます。
$$
\frac{\partial L^{(t)}}{\partial W_{h h}}=\frac{\partial L^{(t)}}{\partial y^{(t)}} \times \frac{\partial y^{(t)}}{\partial h^{(t)}} \times\left(\sum_{k=1}^{t} \frac{\partial h^{(t)}}{\partial h^{(k)}} \times \frac{\partial h^{(k)}}{\partial W_{h h}}\right)
$$
ここで、$\frac{\partial h^{(t)}}{\partial h^{(k)}}$は連続する時間刻みの総乗として計算されます。
$$
\frac{\partial h^{(t)}}{\partial h^{(k)}}=\prod_{i=k+1}^{t} \frac{\partial h^{(i)}}{\partial h^{(i-1)}}
$$
損失関数の勾配を計算するときの乗法係数$\frac{\partial h^{(t)}}{\partial h^{(k)}}$により、いわゆる勾配消失問題と勾配発散問題が発生してしまいます。
Backpropagation Through Time: What It Does and How to Do It
1 重み・バイアス
\begin{gathered}
\frac{\partial E}{\partial W_{(i n)}}=\frac{\partial E}{\partial u^{t}}\left[\frac{\partial u^{t}}{\partial W_{(i n)}}\right]^{T}=\delta^{t}\left[x^{t}\right]^{T} \\
\frac{\partial E}{\partial W_{(o u t)}}=\frac{\partial E}{\partial v^{t}}\left[\frac{\partial v^{t}}{\partial W_{(o u t)}}\right]^{T}=\delta^{\text {out }, t}\left[z^{t}\right]^{T} \\
\frac{\partial E}{\partial W}=\frac{\partial E}{\partial u^{t}}\left[\frac{\partial u^{t}}{\partial W}\right]^{T}=\delta^{t}\left[z^{t-1}\right]^{T} \\
\frac{\partial E}{\partial b}=\frac{\partial E}{\partial u^{t}} \frac{\partial u^{t}}{\partial b}=\delta^{t} \\
\frac{\partial E}{\partial c}=\frac{\partial E}{\partial v^{t}} \frac{\partial v^{t}}{\partial c}=\delta^{\text {out }, t}
\end{gathered}
\begin{gathered}
\frac{\partial E}{\partial u^{t}}=\frac{\partial E}{\partial v^{t}} \frac{\partial v^{t}}{\partial u^{t}}=\frac{\partial E}{\partial v^{t}} \frac{\partial\left\{W_{\text {(out) }} f\left(u^{t}\right)+c\right\}}{\partial u^{t}}=f^{\prime}\left(u^{t}\right) W_{(c u t)}^{T} \delta^{\text {out }, t}=\delta^{t} \\
\delta^{t-1}=\frac{\partial E}{\partial u^{t-1}}=\frac{\partial E}{\partial u^{t}} \frac{\partial u^{t}}{\partial u^{t-1}}=\delta^{t}\left\{\frac{\partial u^{t}}{\partial z^{t-1}} \frac{\partial z^{t-1}}{\partial u^{t-1}}\right\}=\delta^{t}\left\{W f^{\prime}\left(u^{t-1}\right)\right\} \\
\delta^{t-z-1}=\delta^{t-z}\left\{W f^{\prime}\left(u^{t-z-1}\right)\right\}
\end{gathered}
4
パラメータの更新
\begin{gathered}
W_{(\text {in })}^{t+1}=W_{(\text {(in) }}^{t}-\epsilon \frac{\partial E}{\partial W_{(\text {in })}}=W_{(\text {in })}^{t}-\epsilon \sum_{z=0}^{T_{t}} \delta^{t-z}\left[x^{t-z}\right]^{T} \\
W_{(\text {out })}^{+1}=W_{(\text {out })}^{t}-\epsilon \frac{\partial E}{\partial W_{(\text {ou })}}=W_{(\text {out })}^{t}-\epsilon \delta^{\text {out }, t}\left[z^{t}\right]^{T} \\
W^{t+1}=W^{t}-\epsilon \frac{\partial E}{\partial W}=W_{(\text {in })}^{t}-\epsilon \sum_{z=0}^{T_{t}} \delta^{t-z}\left[z^{t-z-1}\right]^{T} \\
b^{t+1}=b^{t}-\epsilon \frac{\partial E}{\partial b}=b^{t}-\epsilon \sum_{z=0}^{T_{t}} \delta^{t-z} \\
c^{t+1}=c^{t}-\epsilon \frac{\partial E}{\partial c}=c^{t}-\epsilon \delta^{\text {out }, t}
\end{gathered}
##コード実装
RNNの実装を行なったgithubです。
weight_init_stdやlearning_rate, hidden_layer_sizeを変更
hidden_layer_size = 16 -> 32
weight_init_std = 1 -> 2
learning_rate = 0.1 -> 0.2
重みの初期化方法を変更(He)
中間層の活性化関数を変更 ReLU(勾配爆発)
中間層の活性化関数を変更 tanh(勾配爆発)
##確認テスト
###確認テスト1
サイズ5×5の入力画像を、サイズ3×3,ストライドは2、パディングは1のフィルタで畳み込んだ時の出力画像のサイズを答えよ。
縦
$$
\frac{5+2 \times 1-3}{2}+1=3
$$
横
$$
\frac{5+2 \times 1-3}{2}+1=3
$$
-> 3×3
###確認テスト2
RNNネットワークには大きく分けて3つの重みがある。1つは入力から現在の中間層を定義する際にかけられる重み、1つは中間層から出力を定義する際にかけられる重みである。残りひとつの重みについて説明せよ。
-> 前の中間層(t−1)から現在の中間層(t)を定義する際にかけられる重み
###確認テスト3
連鎖律の原理を使い、dz/dxを求めよ。
\begin{gathered}
z=t^{2} \\
t=x+y
\end{gathered}
\frac{d x}{d x}=\frac{d x}{d t} \frac{d t}{d x}=2 t \times 1=2(x+y)
-> よって$2(x+y)$
###確認テスト4
下図のy1を$x \cdot z_{0} \cdot z_{1} \cdot w_{\text {in }} \cdot w \cdot w_{\text {out }}$を用いて数式で表わせ。
中間層の出力にシグモイド関数g(x)を作用させよ。
\begin{gathered}
z_{1}=f\left(z_{0} \text { W }+x_{1} \text { Win }+b\right) \\
y_{1}=g\left(z_{1} \text { Wout }+c\right)
\end{gathered}
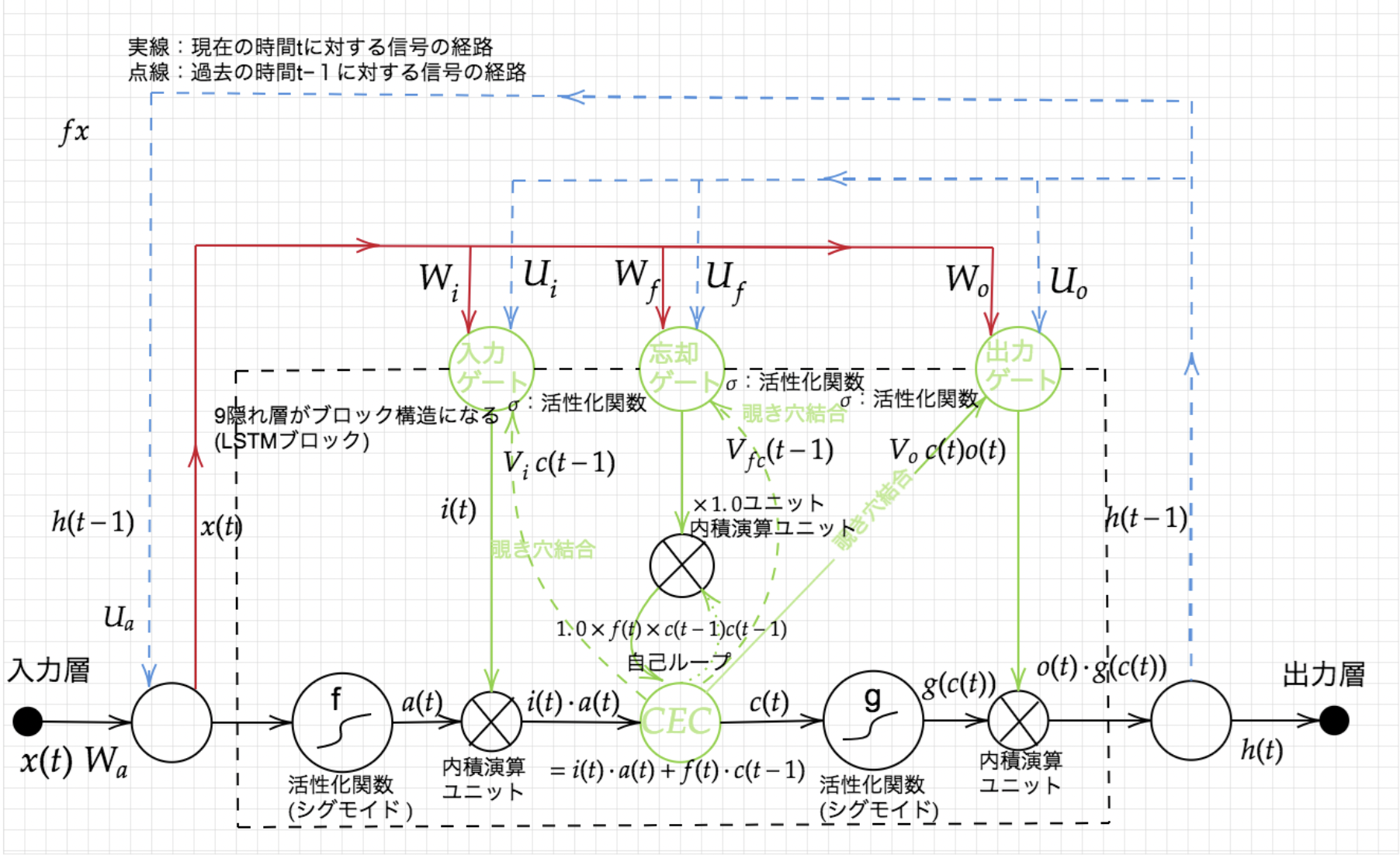
#LSTM(Long Short Term Memory)
LSTM(Long Short-Term Memory)は勾配消失問題を解決する方法として1997年に提唱されたものです。LSTMはRNNの中間層のユニットをLSTM Blockと呼ばれるメモリと3つのゲートを持つブロックに置き換えることで実現されています。
- LSTMの基礎
LSTMのその最も大きな特長は、従来のRNNでは学習できなかった長期依存(long-term dependencies)を学習可能であるところにあります。その最も単純な一例を以下に示します。
$$
\begin{aligned}
&\left(x, a_{1}, a_{2}, \cdots, a_{p-1}, x\right) \
&\left(y, a_{1}, a_{2}, \cdots, a_{p-1}, y\right)
\end{aligned}
$$
通常のRNNでも数十ステップの短期依存(short-term dependencies)には対応できるのですが、1000ステップのような長期の系列は学習することができませんでした。LSTMはこのような系列に対しても適切な出力を行うことができます。
-
CEC
記憶セルのことです。時刻tにおけるLSTMの記憶が格納されており、この部分に過去から時刻t
までにおいて必要な情報が格納されています。 -
入力ゲート
入力ゲートは、a(t)の各要素が新たに追加する情報としてどれだけ価値があるかを判断します。この入力ゲートによって、追加する情報の取捨選択を行います。別の見方をすると、入力ゲートによって重みづけされた情報が新たに追加されることになります。 -
出力ゲート
出力ゲートは、g(c(t))の各要素が次時刻の隠れ状態h(t)としてどれだけ重要かという事を調整します
入力ゲート同様、必要な誤差信号のみ伝達する仕組みを導入し出力の重み衝突問題を解決します。 -
忘却ゲート
記憶セルであるCECに対して、不要な記憶を忘れさせるための役割をするゲートです。
過去の情報がいらなくなる時に、過去の情報を削除する機能を持つために忘却ゲートを使用する。 -
覗き穴結合(peep hole)
ゲートにより遮断された情報を再度活用するためにメモリセルから各ゲートへ情報を流し込むために使用します。
##確認テスト
###確認テスト1
以下の文章にLSTMに入力し空欄に当てはまる単語を予測したいとする。文中の「とても」という言葉は空欄の予測において無くなっても影響を及ぼさないと考えられる。このような場合、どのゲートが作用すると考えられるか。
「映画面白かったね。ところで、とてもお腹が空いたから何か____。」
-> 忘却ゲート
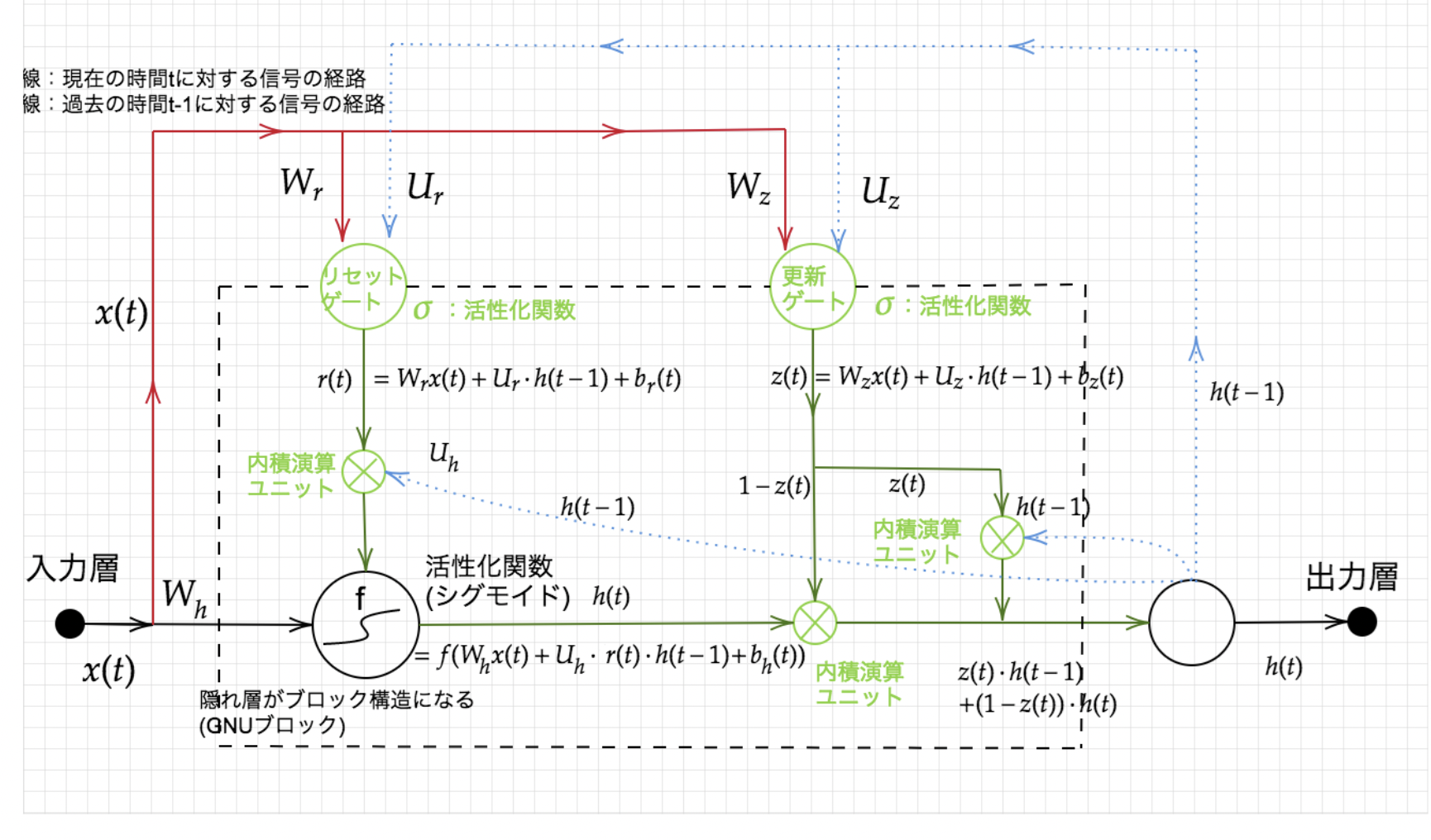
#GRU
LSTMではパラメータ数が多く、計算負荷が高くなることが問題でした。しかし、GRUでは、そのパラメータを大幅に削減し、さらにLSTMより計算量が少なく学習可能です。LSTMと比べて、音声モデリングなどの限定的な用途でのみ同等またはそれ以上の性能を発揮します。LSTMはGRUより厳密に強力なため、GRUで学習できることは全てLSTMで学習可能です。
##確認テスト
###確認テスト1
LSTMとCECが抱える問題について、それぞれ簡潔に述べよ。
-> LSTMは多くのパラメータを持つため、複雑で計算負荷が大きくなってしまいます。CEC自体には学習機能がなく、周りに学習能力のあるゲート(入力ゲート、出力ゲート、忘却ゲート)が必要です。
###確認テスト2
LSTMとGRUの違いを簡潔に説明せよ。
-> LSTMはCEC、入力ゲート、出力ゲート、忘却ゲートを持ちパラメータが多いため計算負荷が大きです。一方、GRUはリセットゲート、更新ゲートを持ち、パラメータが少ないので計算コストがLSTMよりも小さいです。
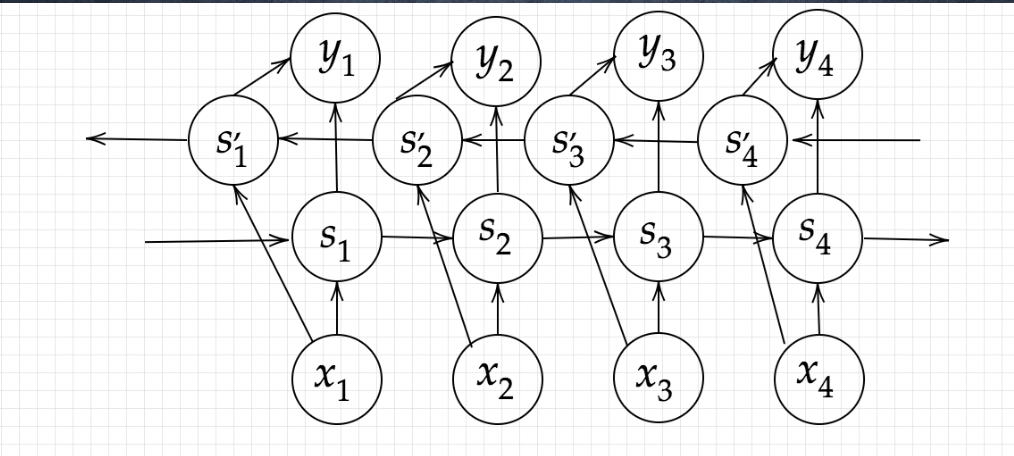
#双方向RNN(BRNN (Bidirectional Recurrent Neural Networks))
2つの正反対の方向の隠れ層を使用します。1つは過去に向かって、もう一つは未来に向かって学習します。これは手書き文字の認識などに効果を発揮します。過去の手書き文字と未来の手書き文字の双方向から現在の文字を予想することができます。
#Seq2Seq
EncoderRNNという入力部とDecoderRNNという出力部を持つRNNです。文章をトークン(単語などの単位)に区切って、EncoderRNNで最初のトークンから順に次のトークンへ時系列的に重みを伝搬させていきます。EncoderRNNの最後の重みの出力をDecoderRNNに学習結果として反映させます。同じく時系列ごとにDecoderRNNの前の時系列の出力(トークン単位)が、DecoderRNNの次の時系列の入力となって、次々とトークンを出力して文章を完成させます。
課題-> 一問一答しかできない。(文脈を学習することができない)
####Encoder RNN
####Decoder RNN
##HRED
Seq2Seq+ Context RNN
seq2seqは一問一答しかできません。問に対して文脈も何もなく、ただ応答が行われる続けます。この時、過去n-1個の発話から次の発話を生成します。Seq2Seqでは、会話の文脈無視で応答されましたが、HREDでは、前の単語の流れに即して応答されるため、Seq2Seqと比較してより人間らしい文章が生成されます。
課題-> HRED は確率的な多様性が字面にしかなく、会話の「流れ」のような多様性がありません。同じコンテキスト(発話リスト)を与えられても、答えの内容が毎回会話の流れとしては同じものしか出せません。
##VHRED
HREDに、VAEの潜在変数の概念を追加したもので、VAEの潜在変数の概念を追加することで解決した構造です。
##Auto Encoder
教師なし学習の一つです。そのため学習時の入力データは訓練データのみで教師データは利用しません。
MNISTの場合、28x28の数字の画像を入れて、同じ画像を出力するニューラルネットワークということになります。
オートエンコーダ構造
入力データから潜在変数zに変換するニューラルネットワークをEncoder逆に潜在変数zをインプットとして元画像を復元するニューラルネットワークをDecoderです。
メリット
次元削減が行えることと、zの次元が入力データより小さい場合、次元削減とみなすことができることです。
##VAE
通常のオートエンコーダーの場合、何かしら潜在変数zにデータを押し込めているものの、その構造がどのような状態かわかりません。VAEはこの潜在変数zに確率分布z∼N(0,1)を仮定したものです。VAEは、データを潜在変数zの確率分布という構造に押し込めることを可能にします。
##確認テスト
###確認テスト1
下記の選択肢から、seq2seqについて説明しているものを選べ。
(1)時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである。
(2)RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(3)構文木などの木構造に対して、隣接単語から表現ベクトル(フレーズ)を作るという演算を再帰的に行い(重みは共通)、文全体の表現ベクトルを得るニューラルネットワークである。
(4)RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである。
-> (2)
###確認テスト2
seq2seqとHRED、HREDとVHREDの違いを簡潔に述べよ。
-> seq2seqは、一文の一問一答に対して処理できるモデルです。
HREDは一問一答ではなく、今までの会話の文脈から答えを導き出せるようにしたモデルです。HREDは会話の流れのような多様性はなく、情報量の乏しいな短い応答しかできないという課題がありました。VHREDはこの課題を、VAEの潜在変数の概念を追加することにより多様性を改善させたモデルです。
###確認テスト3
VAEに関する下記の説明文中の空欄に当てはまる言葉を答えよ。
自己符号化器の潜在変数に____を導入したもの。
-> 確率分布z∼N(0,1)
#Word2Vec
RNNでは、単語のような可変長の文字列をNNに与えることはできない。固定長形式で単語を表す必要があります。そこでWord2Vecでは、OneHotベクトルで重み1行分を単語1つと対応させたニューラルネットワークを採用しています。
メリット-> 大規模データの分散表現の学習が、現実的な計算速度とメモリ量で実現可能にしました。
#Attention Mechanism
前述の通りSeq2Seqでは、長い文章への対応に問題がありました。これを解決するために、入力と出力のどの単語が関連しているかを学ぶAttention Mechanismという仕組みを導入しました。
##確認テスト
###確認テスト1
RNNとWord2vec、Seq2SeqとSeq2Seq+Attentionの違いを簡潔に述べよ。
RNNは時系列データを処理するのに適したネットワークです。
Word2Vecは単語の分散表現ベクトルを得る手法のことです。
Seq2Seqは一つの時系列データから別の時系列データを得るネットワークです。
Attentionは時系列データの中身のそれぞれの関係性に重みをつける手法のことです。
#参考文献