Cyclic Reductionの"くりっくり"の部分
アブストラクト
- ポアソン方程式を直交格子上で離散化すると、三重対角行列を係数行列とする線形連立方程式になる。
- 三重対角行列を係数行列とする線形連立方程式の解法としてCyclic Reduction法がある。
- 今回は一次元のポアソン方程式を対象とする。この場合Cyclic Reduction法は不等間隔格子にも対応できる。
- pythonコードの全体は最後にあります。
ポアソン方程式を不等間隔格子上で離散化する
今回解きたいのは一次元のポアソン方程式
\frac{d^2p}{d x^2}=S
です。$p=p(x)$、$S=S(x)$です。$p$は未知、$S$は既知。境界条件は後述。
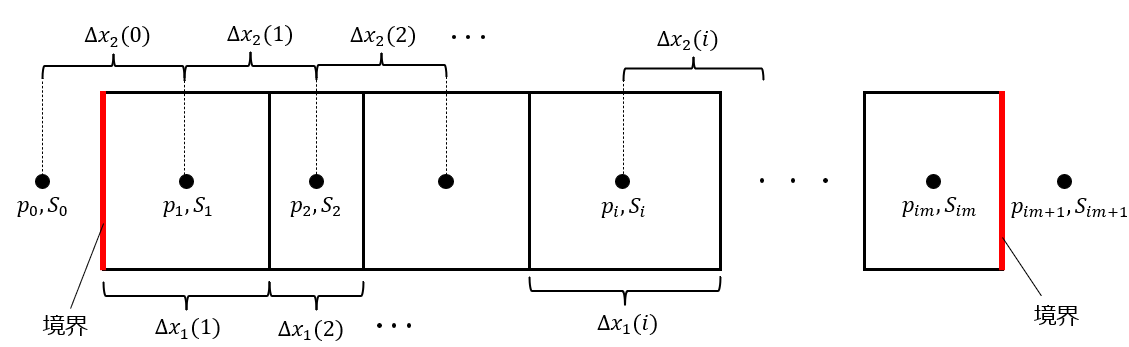
これを図のような一次元の格子上で離散化します。変数は格子中央で定義されます。格子幅は等間隔でなくともよいです。格子幅を$\Delta x_1(i)$、格子中央と格子中央の距離を$\Delta x_2(i)$とします。また、$\Delta x_1(0)=\Delta x_1(1)$、$\Delta x_1(im+1)=\Delta x_1(im)$としておきます。
\frac{(p_{i+1}-p_i)/\Delta x_2(i)-(p_i-p_{i-1})/\Delta x_2(i-1)}{\Delta x_1(i)}=S_i
$i(=0からim+1)$は格子番号。$p_0$と$p_{im+1}$は領域外です。等間隔格子であればよくみる形$(p_{i+1}-2p_i+p_{i-1})/\Delta x^2=S_i$に一致します。
左辺を式変形すると、
\frac{1}{\Delta x_2(i-1)\Delta x_1(i)}p_{i-1}
-\left(\frac{1}{\Delta x_2(i-1)\Delta x_1(i)}+\frac{1}{\Delta x_2(i)\Delta x_1(i)}\right)p_i
+\frac{1}{\Delta x_2(i)\Delta x_1(i)}p_{i+1}
=S_i
\tag{1}
となります。
境界条件
今回は境界で$p=0$とします。
すると$p_0=-p_1$、$p_{im+1}=-p_{im}$なので、(1)の$i=1$番目の式は、
-\left(\frac{2}{\Delta x_2(0)\Delta x_1(1)}+\frac{1}{\Delta x_2(1)\Delta x_1(1)}\right)p_1
+\frac{1}{\Delta x_2(1)\Delta x_1(1)}p_2
=S_1
となります。$i=im$番目も同様。
(補足)
たとえば境界上で$p=1$のときは$p_0=2-p_1$となり、$p_1$の係数に吸収させられません。このような場合、$p_1$を含まない部分は右辺にまわしてしまって、合わせてあらたに$S_1$とすればよいと思います。
Cyclic Reduction法の準備 ~三重対角行列~
(1)を書き下すと、こうなります↓↓
\begin{align}
-\left(\frac{2}{\Delta x_2(0)\Delta x_1(1)}+\frac{1}{\Delta x_2(1)\Delta x_1(1)}\right)p_1
+\frac{1}{\Delta x_2(1)\Delta x_1(1)}p_2
&=S_1\\
\frac{1}{\Delta x_2(1)\Delta x_1(2)}p_{1}
-\left(\frac{1}{\Delta x_2(1)\Delta x_1(2)}+\frac{1}{\Delta x_2(2)\Delta x_1(2)}\right)p_2
+\frac{1}{\Delta x_2(2)\Delta x_1(2)}p_{3}
&=S_2\\
\frac{1}{\Delta x_2(2)\Delta x_1(3)}p_{2}
-\left(\frac{1}{\Delta x_2(2)\Delta x_1(3)}+\frac{1}{\Delta x_2(3)\Delta x_1(3)}\right)p_3
+\frac{1}{\Delta x_2(3)\Delta x_1(3)}p_{4}
&=S_3\\
\vdots \\
&=S_{im}
\end{align}
行列形式で書くと係数行列が三重対角行列になります。
後のために式変形をしておきます。
$i$番目の式に対して、$p_i$の係数で割ります。表記が煩雑になるので$p_{i-1}$の係数は$L_i$、$p_{i+1}$の係数は$R_i$とおいておきます。右辺$S_i$は割ったあとの値を改めて$S_i$と書くとします。
そうすると上式は、行列の形$Ap=S$でかくと係数行列$A$は次のようになります。
A=
\begin{pmatrix}
1 & R_1 & & & \\
L_2 & 1 & R_2 & & \huge{0} \\
& L_3 & 1 & R_3 & \\
& & L_4 & 1 & R_4 & \\
& \huge{0}& & \ddots &\ddots &\ddots\\
& & & & L_{im} & 1
\end{pmatrix}
R= np.zeros(im+2)
L= np.zeros(im+2)
R[1:im ]=(1./dx2[1:im]/dx1[1:im ])/(-1./dx2[0:im-1]/dx1[1:im ]-1./dx2[1:im ]/dx1[1:im ])
L[2:im+1]=(1./dx2[1:im]/dx1[2:im+1])/(-1./dx2[1:im ]/dx1[2:im+1]-1./dx2[2:im+1]/dx1[2:im+1])
S[2:im ]=S[2:im ]/(-1./dx2[1:im-1]/dx1[2:im ]-1./dx2[2:im ]/dx1[2:im ])
R[1] =1./dx2[1 ]/dx1[1] /(-2./dx2[0 ]/dx1[1 ]-1./dx2[1 ]/dx1[1 ])
L[im]=1./dx2[im-1]/dx1[im]/(-1./dx2[im-1]/dx1[im]-2./dx2[im]/dx1[im])
S[1] =S[1] /(-2./dx2[0 ]/dx1[1 ]-1./dx2[1 ]/dx1[1 ])
S[im]=S[im]/(-1./dx2[im-1]/dx1[im]-2./dx2[im]/dx1[im])
Cyclic Reduction法(前半)
Cyclic Reduction法(以下CR法)は次のようなアルゴリズムです。(この記事↓↓を参考にしています)
まず!CR法は格子数が$im=2^N-1$のときに使える手法です。($im=2^N$のときも少しの変更で適応できるが今回はなし。)そのうえで、
\begin{align}
L_{i-1}p_{i-2}+p_{i-1}+R_{i-1}&p_{i}&=S_{i-1}\\
L_{i}p_{i-1}+&p_{i}+R_{i}p_{i+1}&=S_{i}\\
L_{i+1}&p_{i}+p_{i+1}+R_{i+1}p_{i+2}&=&S_{i+1}
\end{align}
$i$番目の式から「$i-1$番目の式を$L_i$倍したもの」と「$i+1$番目の式を$R_i$倍したもの」を引きますと、
\begin{equation}
-L_{i}L_{i-1}p_{i-2}+(1-L_{i}R_{i-1}-R_{i}L_{i+1})p_i-R_iR_{i+1}p_{i+2}=S_i-L_iS_{i-1}-R_iS_{i+1}
\end{equation}
となり、$p_{i-2}$、$p_i$、$p_{i+2}$の式となります。前節と同じように$p_i$の係数で両辺を割れば、
\begin{equation}
L_{i}^{(1)}p_{i-2}+p_i+R_i^{(1)}p_{i+2}=S_i^{(1)}
\end{equation}
となり、元の形にできます。係数と右辺は新たに置きなおしています。
すべての偶数番目の$i$に対してこの操作をすれば式の数は半分になります(正確には$2^N-1$個が$2^{N-1}-1$個になる)。したがって、それを$N-1$回くり返せば、最終的に$p_{2^{N-1}}$に関する一本の式
\begin{equation}
p_{2^{N-1}}=S_{2^{N-1}}^{(N-1)}
\tag{2}
\end{equation}
が得られます。
前半おわり。
N=int(np.log(float(im+1))/np.log(2.))
for n in range(1,N-1+1):
dm=2**(n-1)
for m in range(2**n , im+1-2**n+1 , 2**n):
dc=L[m]*R[m-dm]-1.+R[m]*L[m+dm]
S[m]=(L[m]*S[m-dm]-S[m]+R[m]*S[m+dm])/dc
R[m]=( R[m]*R[m+dm])/dc
L[m]=(L[m]*L[m-dm] )/dc
Cyclic Reduction法(後半)
得られた$p_{2^{N-1}}$から、上の手順を逆にたどってすべての$p_i$を求めていきます。
具体的には、(2)のひとつ前の段階で$p_{2^{N-1}-2^{N-2}}$(と$p_{2^{N-1}}$)の式、$p_{2^{N-1}+2^{N-2}}$(と$p_{2^{N-1}}$)の式があるはずなのでここから$p_{2^{N-1}-2^{N-2}}$と$p_{2^{N-1}+2^{N-2}}$が得られます。すなわち、(添え字だけ見ると)$2^{N-1}$の値から$\pm 2^{N-2}$番目の値が求められます。
次の段階では、ここまで得られた3つの値から、それぞれの$\pm 2^{N-3}$番目の値が求められます。これを繰り返せば($N-1$回ですかね)、すべての$p_i$が計算できます。
for n in range(N-1,0,-1):
dm=2**(n-1)
for m in range(2**n , im+1-2**n+1 , 2**(n+1)):
S[m-dm]=S[m-dm]-L[m-dm]*S[m-2*dm]-R[m-dm]*S[m]
S[m+dm]=S[m+dm]-L[m+dm]*S[m] -R[m+dm]*S[m+2*dm]
p[1:im+1]=S[1:im+1]
# 境界条件
p[0]=-p[1]
p[im+1]=-p[im]
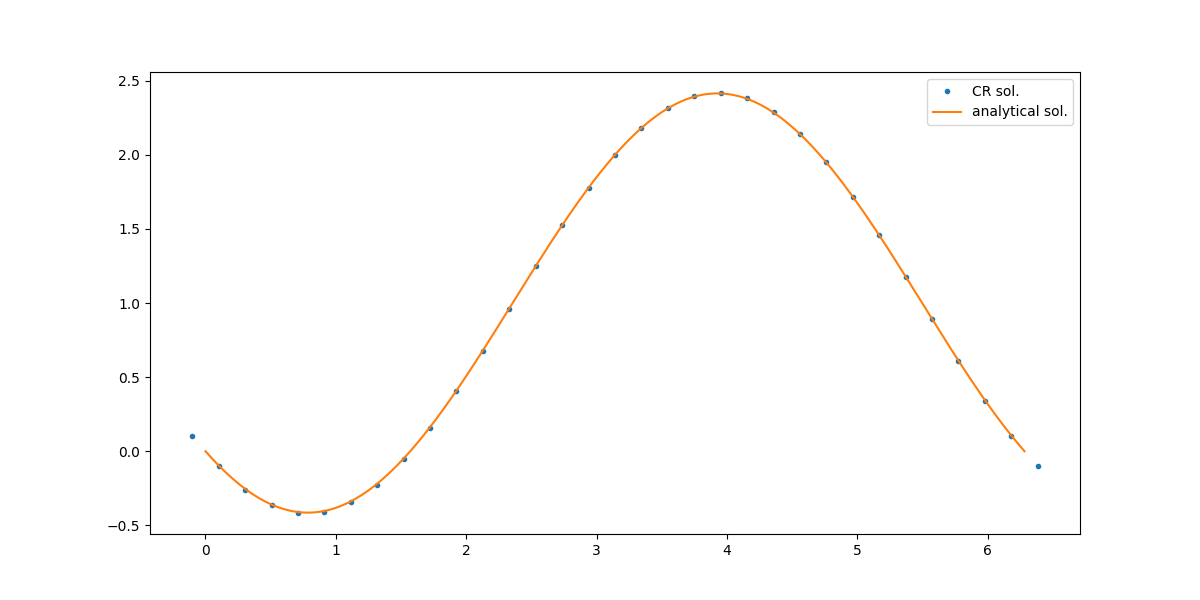
検証
テスト問題として、なんでもいいですが、簡単に、
\begin{equation}
\frac{d^2p}{dx^2}=\cos x +\sin x
\end{equation}
としてやってみます。$0 \leq x \leq 2\pi$で、境界条件を$p(0)=p(2\pi)=0$とすると解は
\begin{equation}
p(x)=-\cos x -\sin x +1
\end{equation}
となるはず。
計算条件
- 格子数$im=2^5-1=31$(領域外含めると$33$)
- 領域サイズ$L=2\pi$
- 一旦、等間隔格子$\Delta x_1=\Delta x_2=L/im$
結果
不等間隔格子の場合
CR法のイイトコロは格子が等間隔でなくてもよいことと、処理がそこそこはやい(らしい↓↓)ことです。
高速なポアソン方程式解法として名高い、高速フーリエ変換やコサイン変換を使うものがあります↓↓
が、これは等間隔格子でのみ適用可能です。その点CR法は不等間隔でもいいというのがいい。計算速度については今回は調べませんが、SOR法とかよりはさすがにはやそうな気がします。
上のテスト問題を格子幅を変えてやってみます。
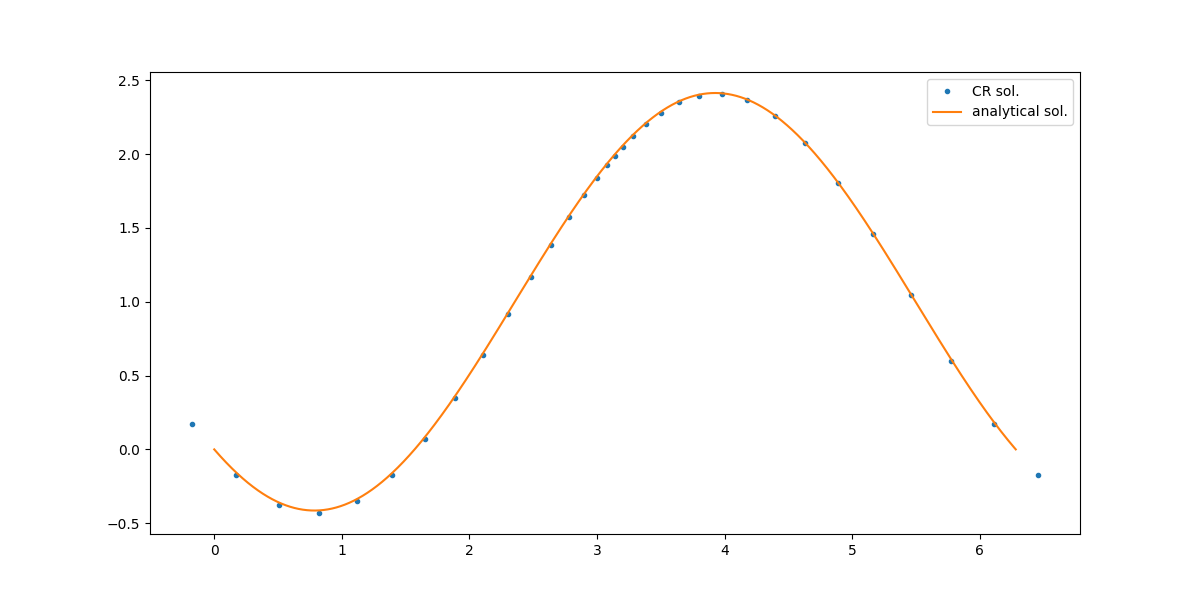
ケース1
等間隔($1:1:1\cdots$)だったのを$0.5:0.5:2\cdots$にします。
\begin{equation}
\Delta x_1(i)=
\begin{cases}
2 L/im & \text{if $i$は3の倍数,} \\
0.5 L/im & \text{if $i$は3の倍数でない.}
\end{cases}
\end{equation}
境界近くだけ$\Delta x_1=L/im$にしておきます。その他の条件は上と同じ。
# 不等間隔格子(ケース1)------------------------------
dx1[:]=Lx/float(im)
dx1[3:im-1:3]=2.*Lx/float(im)
dx1[4:im:3]=0.5*Lx/float(im)
dx1[5:im:3]=0.5*Lx/float(im)
結果
できていそうです。少し精度悪いか?格子数を増やせば大丈夫...。間違いがあれば教えてください。
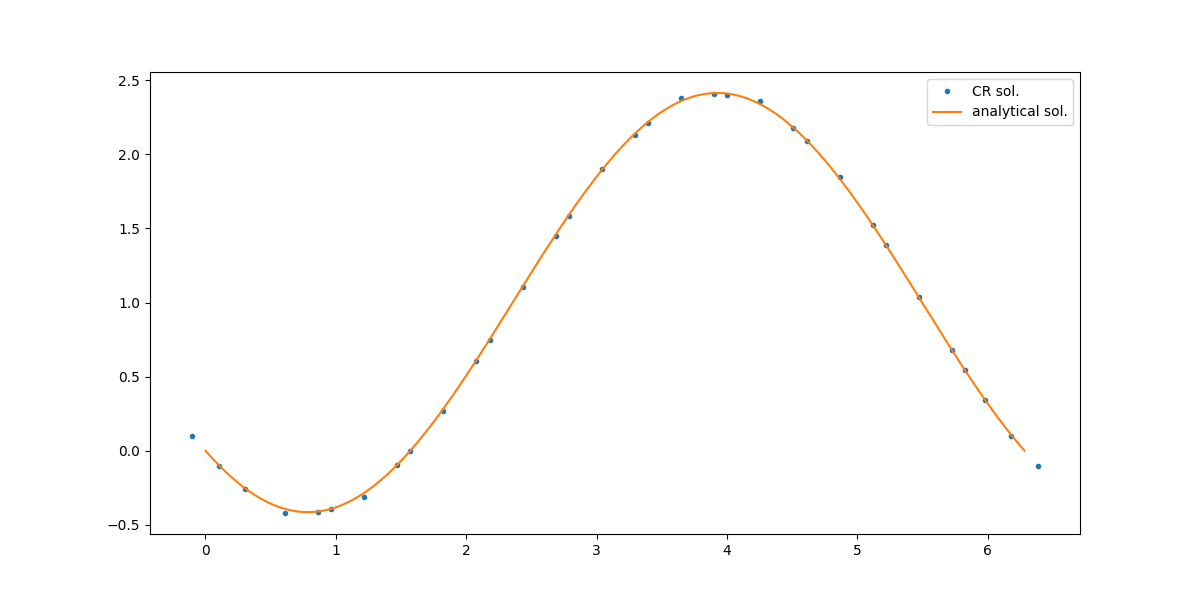
ケース2
領域の端で大きめの格子で、中央に近づくにつれて線形に細かくなっていくようにします。
- 端 :$\Delta x_1(1)=\Delta x_1(im)=1.7L/im$
- 中央:$\Delta x_1((im+1)/2)\risingdotseq 0.25L/im$
# 不等間隔格子(ケース2)------------------------------
dmax=1.7*Lx/float(im) # L/im < dmax < 2L/(im+1)
dmin=2./float(im-1)*(Lx-float(im+1)/2.*dmax)
dx1[1]=dmax
dx1[int((im+1)/2)]=dmin
for i in range(2,int((im+1)/2)):
dx1[i]=(dmin-dmax)/float((im+1)/2-1)*float(i-1)+dmax
dx1[int((im+1)/2+1):im+1:1]=dx1[int((im+1)/2-1):0:-1]
dmaxを自分で決めればあとは勝手に決まるようにしています。L/im < dmax < 2L/(im+1)の範囲でないと、dminがdmaxより大きくなったりdminが負の値になったりするので注意。
結果
おしまい(Unfortunately)
うまく実装できていそうでよかったです。短いコードで、特別なライブラリも使わず実装できるかっこいいアルゴリズムだと思います。
残念ながら二次元とか三次元のポアソン方程式をCR法で解こうとなると、難しいようです。二次元の場合は調べるといくつか出てきますが、等間隔格子の場合ばかりです。等間隔ならFFTでいいからなあ。本記事で言うところの$R_i$とか$L_i$が二次元の場合は行列になるから逆行列とかを計算しないといけなくて難しい、とか?どなたか教えてください。
なので、$x$方向に等間隔、$y$方向に不等間隔みたいな格子のときに、$x$方向はFFT、$y$方向はCR法で解く、みたいなことをしたい。そのうちやります。
コード全体
import numpy as np
import matplotlib.pyplot as plt
im=32-1
Lx=2.*np.pi
dx1=np.zeros(im+2)
dx2=np.zeros(im+2)
x =np.zeros(im+2)
p =np.zeros(im+2)
# 等間隔格子----------------------------
dx1[:]=Lx/float(im)
# -------------------------------------
# # 不等間隔格子(ケース1)-------------------
# dx1[:]=Lx/float(im)
# dx1[3:im-1:3]=2.*Lx/float(im)
# dx1[4:im:3]=0.5*Lx/float(im)
# dx1[5:im:3]=0.5*Lx/float(im)
# # ----------------------------------------
# # 不等間隔格子(ケース2)------------------------------
# dmax=1.7*Lx/float(im) # L/im < dmax < 2L/(im+1)
# dmin=2./float(im-1)*(Lx-float(im+1)/2.*dmax)
# dx1[1]=dmax
# dx1[int((im+1)/2)]=dmin
# for i in range(2,int((im+1)/2)):
# dx1[i]=(dmin-dmax)/float((im+1)/2-1)*float(i-1)+dmax
# dx1[int((im+1)/2+1):im+1:1]=dx1[int((im+1)/2-1):0:-1]
# #--------------------------------------------------------
dx1[0]=dx1[1]
dx1[im+1]=dx1[im]
x[0]=-0.5*dx1[0]
for i in range(1,im+2):
x[i]=x[i-1]+0.5*(dx1[i-1]+dx1[i])
dx2[0:im+1]=x[1:im+2]-x[0:im+1]
S= np.zeros(im+2)
for i in range(0,im+2):
S[i]=np.cos(x[i])+np.sin(x[i])
S[0]=0.
S[im+1]=0.
R= np.zeros(im+2)
L= np.zeros(im+2)
R[1:im ]=(1./dx2[1:im]/dx1[1:im ])/(-1./dx2[0:im-1]/dx1[1:im ]-1./dx2[1:im ]/dx1[1:im ])
L[2:im+1]=(1./dx2[1:im]/dx1[2:im+1])/(-1./dx2[1:im ]/dx1[2:im+1]-1./dx2[2:im+1]/dx1[2:im+1])
S[2:im ]=S[2:im ]/(-1./dx2[1:im-1]/dx1[2:im ]-1./dx2[2:im ]/dx1[2:im ])
R[1] =1./dx2[1 ]/dx1[1] /(-2./dx2[0 ]/dx1[1 ]-1./dx2[1 ]/dx1[1 ])
L[im]=1./dx2[im-1]/dx1[im]/(-1./dx2[im-1]/dx1[im]-2./dx2[im]/dx1[im])
S[1] =S[1] /(-2./dx2[0 ]/dx1[1 ]-1./dx2[1 ]/dx1[1 ])
S[im]=S[im]/(-1./dx2[im-1]/dx1[im]-2./dx2[im]/dx1[im])
N=int(np.log(float(im+1))/np.log(2.))
for n in range(1,N-1+1):
dm=2**(n-1)
for m in range(2**n , im+1-2**n+1 , 2**n):
dc=L[m]*R[m-dm]-1.+R[m]*L[m+dm]
S[m]=(L[m]*S[m-dm]-S[m]+R[m]*S[m+dm])/dc
R[m]=( R[m]*R[m+dm])/dc
L[m]=(L[m]*L[m-dm] )/dc
for n in range(N-1,0,-1):
dm=2**(n-1)
for m in range(2**n , im+1-2**n+1 , 2**(n+1)):
S[m-dm]=S[m-dm]-L[m-dm]*S[m-2*dm]-R[m-dm]*S[m]
S[m+dm]=S[m+dm]-L[m+dm]*S[m] -R[m+dm]*S[m+2*dm]
p[1:im+1]=S[1:im+1]
# 境界条件
p[0]=-p[1]
p[im+1]=-p[im]
fig1=plt.figure(figsize=(12,6))
ax1= fig1.add_subplot()
ax1.plot(x,p,'.',label='CR sol.')
x=np.linspace(0,Lx,10000)
print(x)
ax1.plot(x,-np.sin(x)-np.cos(x)+1.,label='analytical sol.')
ax1.legend()
# plt.savefig('CR.png')
plt.show()