はじめに
前編「グラフ最適化をマスターしよう!」では、グラフ最適化の全体像を説明し、独自の汎用グラフ最適化ライブラリ(graph_solver)を紹介しました。今回はこのライブラリを利用して、リー群ベースのループ閉じ込み (Loop Closure / Loop Closing)の解法について解説したいと思います。
ループ閉じ込みとは?
ループ閉じ込みは、SLAM(Simultaneous Localization and Mapping)研究において重要なテーマの一つです。移動体が未知の環境で自己位置推定と地図作成を行うSLAMのプロセスにおいて、誤差が蓄積されて地図と自己位置推定の間に不整合が生じる場合に、その不整合を修正する手法を指します。
ループ閉じ込みの例
わかりやすく説明するために、簡単なループ閉じ込みの例を示します。
以下の図では、緑の円形のロボットが未知の環境を探索し、車輪オドメトリから自己位置を累積的に算出します。車輪オドメトリの誤差が存在し、この誤差はロボットの移動(青いエッジ)とともに蓄積され、自己位置の信頼性が低下していきます。
上の図に、自己位置の信頼性(ロボットが高い確率で存在する領域)はピンクの楕円で示します。誤差伝播(Error Propagation)により、誤差は徐々に蓄積され、楕円が拡大していきます。
蓄積された誤差を修正するために、ロボットが同じ場所を再度通過することを検出し(赤いエッジのようにループを検出)、自己位置を修正することができます。ただし、ループのみを修正すると、他の箇所に不整合が発生する可能性があるため、グラフ最適化の手法を使用して、全体(赤いエッジと青いエッジ)の誤差を最小化するように補正する必要があります。
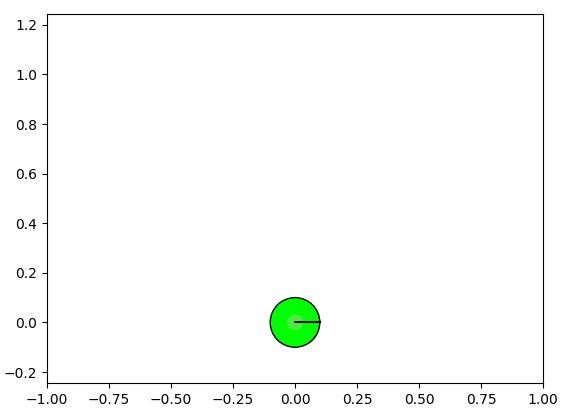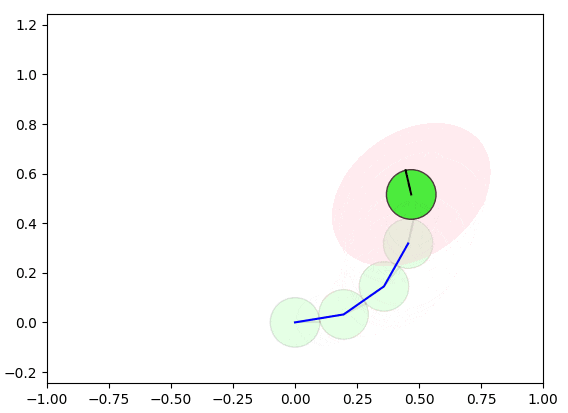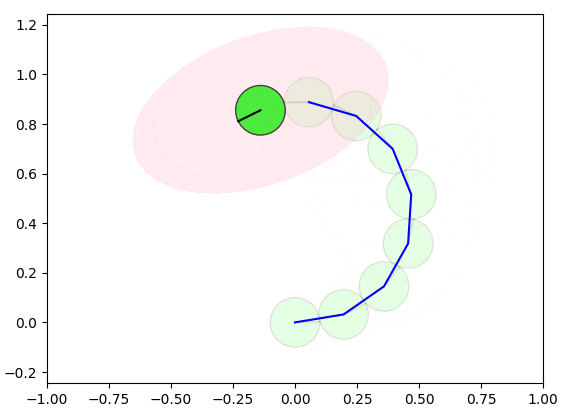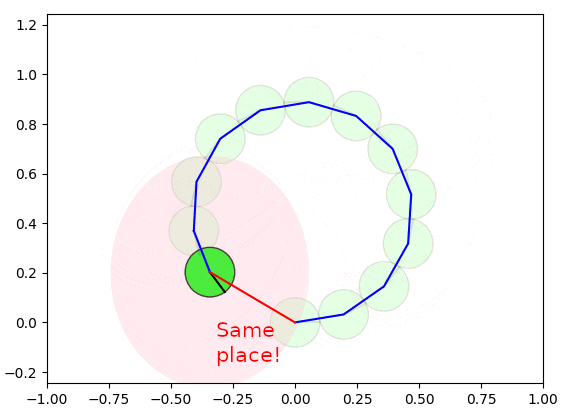
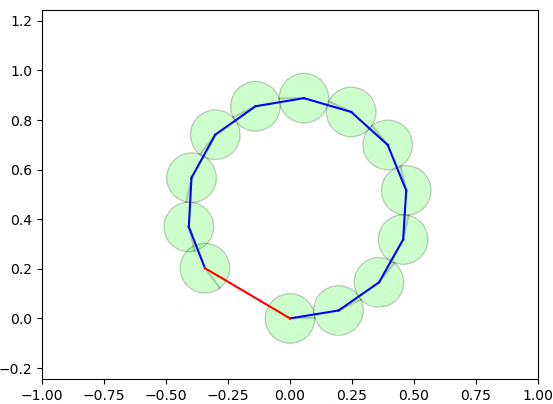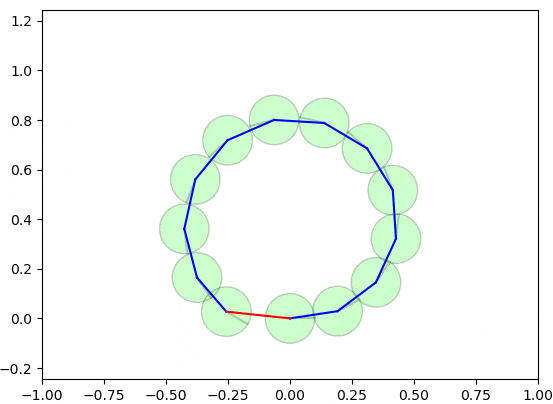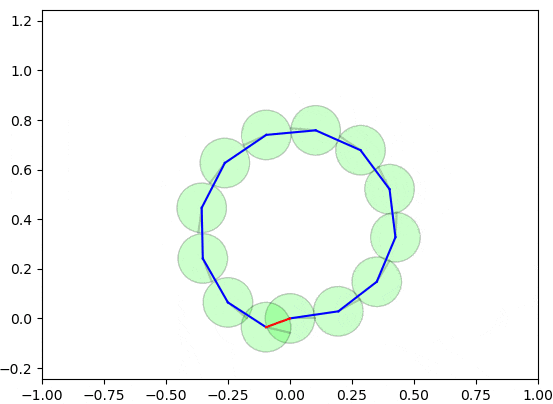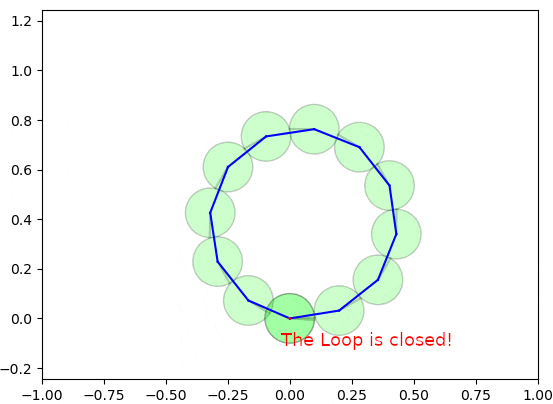
以下の図は、グラフ最適化の手法によるループ閉じ込みが実施される様子を示しています。
実際は2〜3ステップぐらいで収束可能ですが、理解しやすいようにゆっくり収束するようにしています。
グラフベースのループ閉じ込み
なかなか面白いと思いませんか?全体的な整合性を維持しつつ、誤差を修正しましたね。本章では、このデモで使用したループ閉じ込みのアルゴリズムを詳細に説明します。
$$
\newcommand{\skew}[1]{[{#1}]_{\times}} %skew matrix
\newcommand{\so}[1]{ \mathfrak{so}{(#1)} } %lie algebra so3
\newcommand{\se}[1]{ \mathfrak{se}{(#1)} } %lie algebra se3
\newcommand{\norm}[1]{|{#1}|} %norm
$$
グラフは頂点とエッジから構成されるデータ構造ですので、まず、ループ閉じ込み問題における頂点とエッジを定義します。
頂点
この問題では、グラフの頂点が一定間隔で記録されたロボットの過去の自己位置$T$を表しています。$T$は$SE(n)$※に属します。
$$
V = \lbrace T_1, T_2, ..., T_n \mid T_i\in SE(n) \rbrace
$$
※2Dと3Dの問題のとき、$T$はそれぞれ$SE(2)$と$SE(3)$に属します。
エッジ
エッジには、異なる頂点間の相対位置(誤差を含む)が格納されています。連続する頂点間では、オドメトリに基づいて算出された相対位置が把握できます。また、ループが検出された頂点間でも相対位置はセンサーから観測可能です。したがって、エッジ$e_k$の残差$r_k$は以下のように定義できます。
$$
\begin{aligned}
r_k(T_i, T_j) &= \log(Z_k^{-1} (T_i^{-1} T_j) )^{\vee} \\
&= \exp(\widehat{T_j \boxminus T_i}) \boxminus Z_k
\end{aligned}
\tag{1}
$$
残差$r_k$は$\se{n}$に属し、頂点$T_i$と$T_j$間の相対位置($\exp{\widehat{(T_j \boxminus T_i})}$)とセンサーから観測された相対位置($Z_k$)の差分を表します。
また、$\boxminus$は差分演算を示す記号であり、リー群の差分演算は以下に定義されます。
$$
T_j \boxminus T_i = \log(T_i^{-1} T_j)^{\vee}
\tag{2}
$$
ちなみに、$\boxplus$は更新演算の記号であり、リー群の更新演算は以下に定義されます。
$$
T \boxplus \delta = T \exp{(\hat{\delta})}
\tag{3}
$$
ヤコビ行列
前編の説明に従って、残差のヤコビ行列を算出することができれば、ガウス・ニュートン法を使用して、すべてのエッジの残差の合計を最小化することで、グラフ最適化問題を解決することができます。
以下では、ヤコビ行列の計算方法について議論します。
ヤコビ行列の定義
ヤコビ行列は、ある多変数関数$F$のパラメータが微小な量$\delta$だけ更新した場合に、その関数の出力値がどれだけ変化するかを表すものです。
$F(x)$のパラメータ$x$が$\mathbb{R}^n$に属する場合、ヤコビ行列$J$は以下のように定義されます。
$$
\begin{aligned}
J &= \frac{F(x_0 + \delta) - F(x_0)}{\delta}
\end{aligned}
\tag{4}
$$
しかし、パラメータが$SE(n)$に属する場合、$SE(n)$上の更新($\boxplus$)と差分($\boxminus$)の定義は$\mathbb{R}^n$上と異なるため、ヤコビ行列の定義を以下のように書き直します。
$$
\begin{aligned}
J &= \frac{F(T_0 \boxplus \delta) \boxminus F(T_0)}{\delta}
\end{aligned}
\tag{5}
$$
式(5)に式(2)と(3)を代入すると、$SE(n)$のヤコビ行列は以下のように計算できます。
$$
J = \frac{\log(F(T_0)^{-1}F(T_0 \exp(\hat{\delta})))^{\vee}}{\delta}
\tag{6}
$$
残差のヤコビ行列
ようやく、残差のヤコビ行列を議論する準備が整いました。式(1)の残差定義を式(6)に代入することで、ヤコビ行列を計算することができます。
式(1)の$r_k$には2つのパラメータがあるため、それぞれのヤコビ行列を以下のように計算することができます。
Tiに関するヤコビ行列
式(6)に式(1)を代入して、$T_i$に関するヤコビ行列$J_i$を以下のように計算できます。
$$
\begin{aligned}
J_i
&= \frac{\log((Z_k^{-1} T_i^{{-1}} T_j)^{-1}(Z_k^{-1}(T_i\exp(\hat{\delta}))^{{-1}}T_j))^{\vee}}{\delta} \\
&= -\frac{ \log(T_{ji} \exp ( \hat{\delta} )T_{ji}^{-1})^{\vee}}{\delta} \\
&= -\frac{ \log( \exp (T_{ji} \hat{\delta} T_{ji}^{-1}))^{\vee}}{\delta} \\
\end{aligned}
\tag{7}
$$
ここで、$T_{ji} = T_j^{-1}T_i$
$\hat{\delta}$の定義は、$\delta$が$\se{2}$と$\se{3}$に属する場合で異なるため、それぞれについて議論する必要があります。しかし、記事が長くなりすぎないように、ここでは$\se{3}$のみ説明します。
- 式(7)の2行目を3行目に変形できる理由は、前編の「リー群による回転表現」の式(9)を参考してください。
- $\se{2}$の場合のヤコビ行列の証明について、MathematicalRoboticsのgraph_optimization.pdfを参考してください。
se(3)の場合
以前の記事「3D剛体変換群」の式(10)より、$\delta$は微小並進$\rho$と微小回転$\omega$から構成された6次元ベクトルであり、$\hat{\delta}$は以下のように定義されます。
$$
\hat{\delta} = \begin{bmatrix}
\skew{\omega} & \rho \\
0 & 0
\end{bmatrix}
$$
$\hat{\delta}$を式(7)に代入すると、$J_i$を計算することができます。
$$
\begin{aligned}
J_i
&=
-\frac{\log \biggl( \exp \biggl( T_{ji}
\begin{bmatrix}
\skew{\omega} & \rho \\
0 & 0
\end{bmatrix}
T_{ji}^{{-1}} \biggr) \biggr)^{\vee}}{[\rho, \omega]^T} \\
&=
-\begin{bmatrix}
R_{ji} & \skew{t_{ji}} R_{ji} \\
0 & R_{ji}
\end{bmatrix}
\end{aligned}
\tag{8}
$$
- 式(8)の計算の証明は、付録に記載されています。
Tjに関するヤコビ行列
式(6)に式(1)を代入して、$T_i$に関するヤコビ行列を以下のように計算できます。
$$
\begin{aligned}
J_i
&= \frac{\log((Z_k^{-1} T_i^{{-1}} T_j)^{-1}(Z_k^{-1}T_i^{{-1}}T_j\exp(\hat{\delta})))^{\vee}}{\delta} \\
&= \frac{\log( T_j^{-1} T_i Z_kZ_k^{-1}T_i^{{-1}}T_j\exp(\hat{\delta}))^{\vee}}{\delta} \\
&= I \\
\end{aligned}
\tag{9}
$$
ここで、$I$は単位行列です。
$\hat{\delta}$が完全に消えたため、$\se{2}$と$\se{3}$の場合のいずれも同じ結果になります。
Python実装
上記の内容を完全に理解した後、独自のグラフ最適化ライブラリを使用して、以下のようにループ閉じ込みのエッジを実装できます。
以下に、3Dのエッジの実装例を示します。
# BaseEdgeを継承し、3Dループ閉じ込みのEdgeを実装します。
class Pose3dbetweenEdge(BaseEdge):
def __init__(self, link, z, omega=np.eye(6), kernel=None, color='black'):
super().__init__(link, z, omega, kernel)
self.color = color #可視化するときの色
def residual(self, vertices):
Ti = vertices[self.link[0]].x # 頂点Ti
Tj = vertices[self.link[1]].x # 頂点Tj
Tij = np.linalg.inv(Ti) @ Tj
r = logSE3(np.linalg.inv(self.z) @ Tij) # rの計算 式(1)
Tji = np.linalg.inv(Tij)
Rji, tji = makeRt(Tji)
J = np.zeros([6, 6])
J[0:3, 0:3] = -Rji # J_iの計算 式(8)
J[0:3, 3:6] = -skew(tji).dot(Rji) # J_iの計算 式(8)
J[3:6, 3:6] = -Rji # J_iの計算 式(8)
return r, [J, np.eye(6)] # J_jの計算 式(9)
2Dのエッジの実装については、直接GitHubを参照してください。
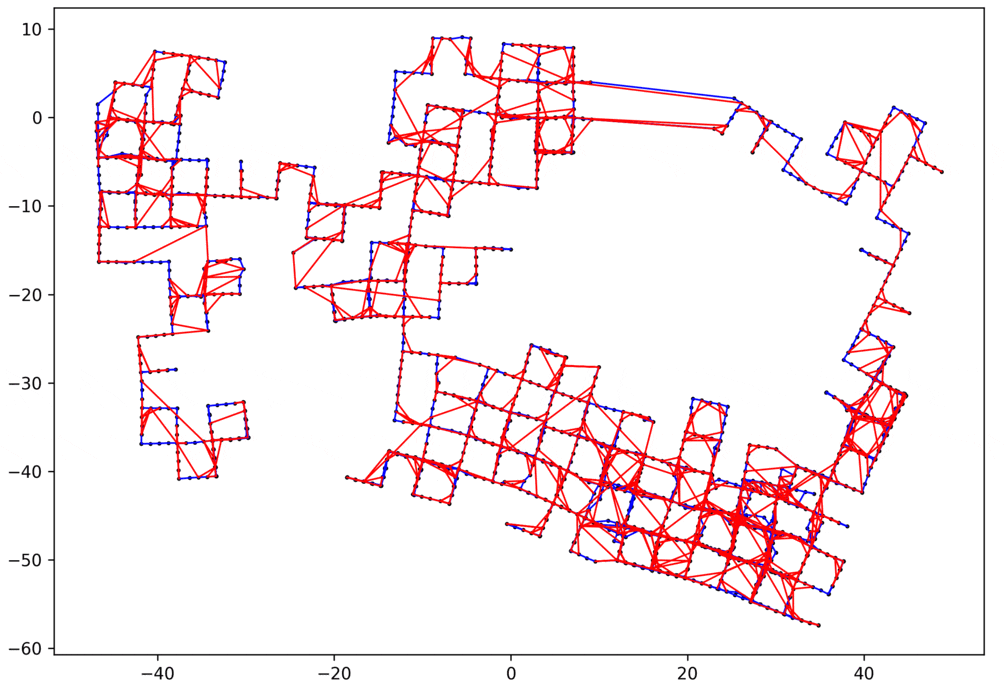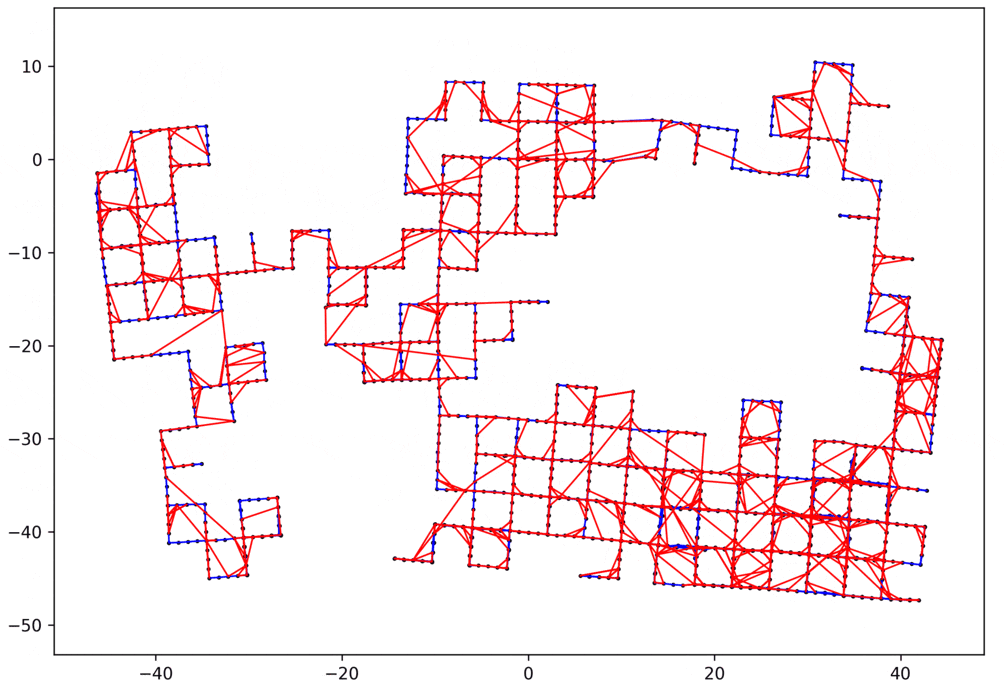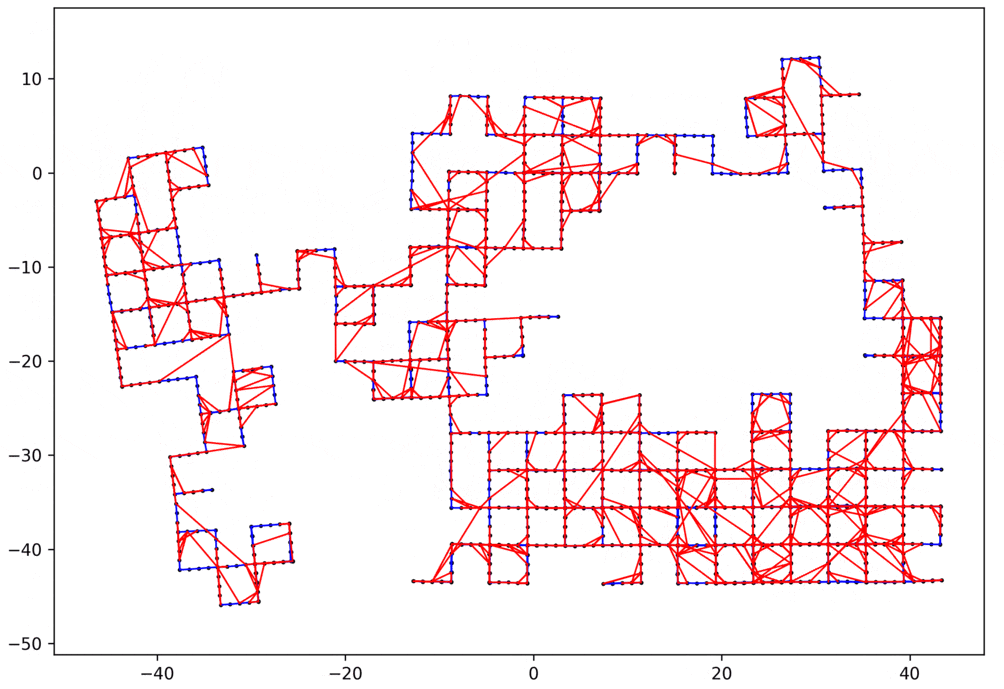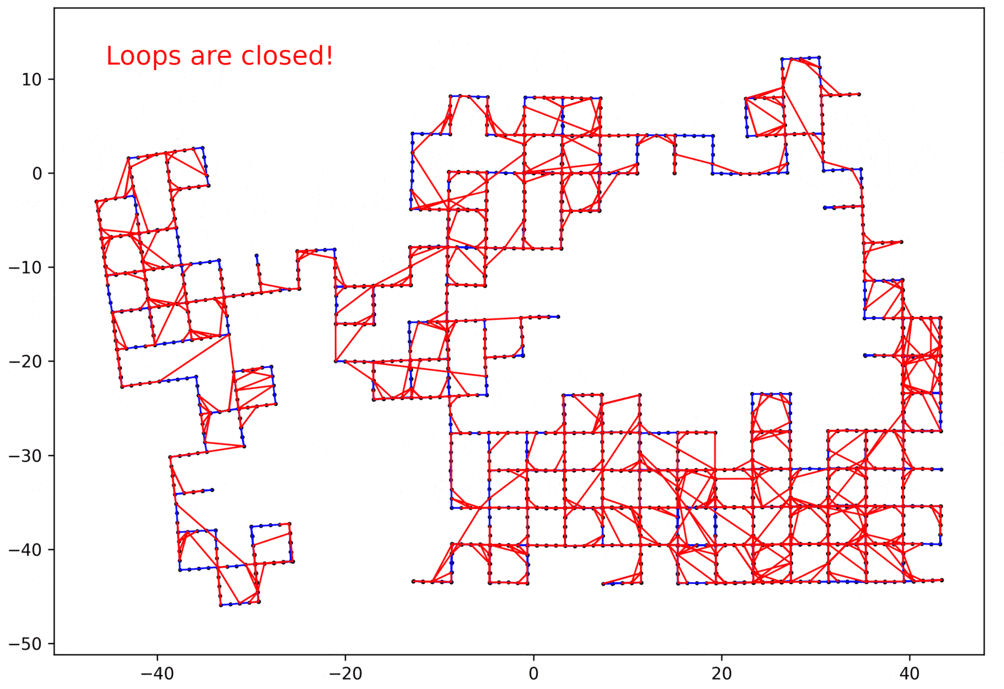
デモ
以上のように実装できたら、簡単な問題だけでなく、かなり複雑なループ閉じ込み問題も解くことができます。以下にいくつかの例を示します。
- 赤いエッジ:ループのエッジ
- 青いエッジ:ループじゃないエッジ
2Dのループループ閉じ込み問題
データ:manhattanOlson3500 1
データ:ringCity 1

3Dのループループ閉じ込み問題
データ:sphere2500 1
球面上を移動するロボットのシミュレーションを行います。自己位置の誤差があり、初期値が崩れた状態から始めますが、ループ閉じ込めによって完璧な球面に戻りました。

まとめ
本文では、リー群ベースのループ閉じ込みの解法について解説しました。結論だけでなく、すべての計算式の詳細証明も示しました。単に実装して使用するだけでなく、より深い理論的な根拠を理解できましたでしょうか。数学的な根拠を完全に理解することで、他の課題にも適用できるようになりますので、ぜひ、リー群ベースのループ閉じ込みを完全理解しましょう。
付録
式(8)の計算の証明を以下に示します。
$$
\begin{aligned}
J_i
&=
-\frac{\log \biggl( \exp \biggl( T_{ji}
\begin{bmatrix}
\skew{\omega} & \rho \\
0 & 0 \
\end{bmatrix}
T_{ji}^{{-1}} \biggr) \biggr)^{\vee}}{[\rho, \omega]^T} \\ %line1
&=
-\frac{\log \biggl( \exp \biggl( \begin{bmatrix}
R_{ji} & t_{ji} \\
0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
\skew{\omega} & \rho \\
0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
R_{ji}^T & -R_{ji}^T t_{ji} \\
0 & 1 \\
\end{bmatrix} \biggr) \biggr)^{\vee}}{[\rho, \omega]^T} \\ %line2
&=
-\frac{\log \biggl( \exp \biggl(
\begin{bmatrix}
R_{ji} \skew{\omega} R_{ji} ^T & -R_{ji} \skew{\omega} R_{ji} ^T t_{ji} +R_{ji} \rho \\
0 & 0 \
\end{bmatrix}\biggr) \biggr)^{\vee}}
{[\rho, \omega]^T} \\ %line3
&=
-\frac{\log \biggl( \exp \biggl(
\begin{bmatrix}
\skew{R_{ji} \omega} & - \skew{R_{ji} \omega} t_{ji} +R_{ji} \rho \\
0 & 0 \
\end{bmatrix}\biggr) \biggr)^{\vee}}
{[\rho, \omega]^T} \\ %line4
\end{aligned}
$$
exp内の行列をベクトルの$\wedge$の形式に書き直して、logとexpを消去します。
$$
\begin{aligned}
&=
-\frac{\log \biggl( \exp \biggl(
\widehat{
\begin{bmatrix}
R_{ji} \rho + \skew{t} R_{ji} \omega \\
R_{ji} \omega
\end{bmatrix}
}
\biggr) \biggr)^{\vee}}{[\rho, \omega]^T} \\
&=
-\frac{\begin{bmatrix}
R_{ji} \rho + \skew{t} R_{ji} \omega \\
R_{ji} \omega
\end{bmatrix}
}{[\rho, \omega]^T} \\
&=
-\frac{
\begin{bmatrix}
R_{ji} & \skew{t_{ji}} R_{ji} \\
0 & R_{ji}
\end{bmatrix}
\begin{bmatrix}
\rho \\
\omega
\end{bmatrix}
}{[\rho, \omega]^T} \\
&=
-\begin{bmatrix}
R_{ji} & \skew{t_{ji}} R_{ji} \\
0 & R_{ji}
\end{bmatrix}
\end{aligned}
$$
すべての実装はgithubに公開していますので、ご自由に参考にしてください。
- グラフ最適化ライブラリ: graph_optimization/graph_solver.py
- 2Dのデモ: graph_optimization/demo_g2o_se2.py
- 3Dのデモ: graph_optimization/demo_g2o_se3.py