はじめに
**行列の固有値・固有ベクトルを数値的に求めるためのアルゴリズムをネット等で調べ出すと,
多くの手法がめまぐるしく出てきます。**初学者の方は内心ウンザリしてしまうこともあると思います...。
そこで,本記事では行列の固有値問題への取り組み方について私が知っていることをまとめ,
初学者の方が固有値問題を学ぶ際に役立つような初等的なロードマップを提示したいと思います。
図として一枚にまとめると以下のようになります。
足りない箇所は随時更新していきます。
(注意)おそらく"業界"ではジョーシキのことだと思いますので,玄人の方は満足できないと思います。
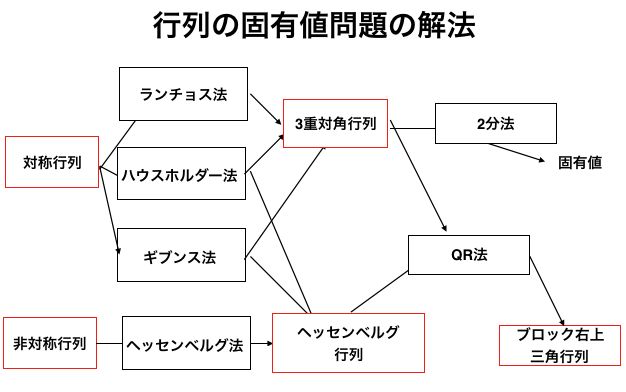
図. ざっくりとしたロードマップ。中間形である3重対角行列やヘッセンベルグ行列へといったん変換するのが標準的なアプローチ。
どんな人向け?
● 行列の固有値・固有ベクトルの数値計算について学びたい方
● 固有値問題の解法をざっくり俯瞰してみたい方
内容
1. 固有値問題の導入: 5x5以上の行列の固有値問題は代数的には解けない!どうする?
2. 相似変換に注目
3. 中間形への変換
4. 中間形へ変換しない解法: ヤコビ法,べき乗法
5. QR法: QR分解のpythonコード
なお,本記事にはさまざまな行列名がでてきます。知らない場合はこちらを参考にしてください。
[Pythonによる科学・技術計算] 数値線形代数でヒンパンに出てくる行列の一覧
1. 固有値問題
N次元の正方行列$A$
$$Ax = \lambda x$$
特性方程式
$$det(A-\lambda E) = 0$$
N次の代数方程式になるが,これによって解が求まるのは4x4行列までです。**N=5以上の場合(5次以上の方程式の場合)は一般解を求める代数的な手続き(加減乗除とべき根(平方根,立方根など))は存在しません("ガロア理論"というものから説明されるそうです)。**固有値問題を解くには他の方法が必要となります。なお,N=1は線形方程式,N=2は二次方程式,N=3はCardanoの方法による解,そしてN=4はFerrariの方法と呼ばれる手順で求めることが可能です。
2. 相似変換に着目
行列Aに相似変換を繰り返し行列を徐々に上三角行列(対角行列)に近づけていく,という方法が一般的な固有値計算法です。
$ A x = \lambda x$
Pを正則行列($det(P)\ne0)$ とすると,
相似変換]
$$A->B = P^{-1}AP$$
に対して固有値は不変です。実際,
$A = PBP^{-1}$を上の固有方程式に代入すると
$PBP^{-1} x = \lambda x$より,
$B(P^{-1} x) = \lambda (P^{-1}x)$となり相似変換に対する固有値不変性が確かめられます。
ただし,固有ベクトルは同じではありません。求まる固有ベクトルはもとの$x$ではなく$P^{-1} x$となっています。
シューア(Schur)の定理
一般の複素行列Aはユニタリ行列Uによる相似変換$U^\dagger$によって上三角行列Sにすることができます。
$$S=UAU^\dagger $$
また,
$$A=USU^\dagger $$
をSchur分解といいます。
Sの対角成分がAの固有値です。また,U=[u_1,u_2,...,u_N]の列ベクトル$u_j$をSchurベクトルと呼びます。。
定理: 実行列Aについては直交行列Qによる相似変換$Q^TAQ$によって準(擬)上三角行列(ブロック上三角行列で対角ブロックの次数がたかだか2のもの)にすることができます。
$$A=QSQ^T $$
Sの対角ブロックの固有値がAの固有値です。
Uを有限回の四則・開平演算によって求めることができないことが証明されています。したがってなんらかの反復計算によってUの近似値を求める必要があります。
理・工学で現れる行列は実対称行列やエルミート行列が多いです。
Aがエルミート行列(実対称行列)のときはユニタリ行列(直交行列)で対角行列にすることができます。ユニタリ変換で固有ベクトルが計算でき,固有値が実数であるという事情から一般の行列よりも扱いやすいです。
3. 中間形への変換
標準的な解法は,有限回のユニタリ変換により中間形の行列$B$へと変換し,そこから反復計算により固有値を計算します。こうする理由は1反復あたりの計算量を減らすためです。
そこで計算の流れは,
行列A ==(ユニタリ行列による相似変換を行う)=> 中間形B ==(収束するまで反復計算を行う)==> 固有値計算
となります。
中間形Bは上ヘッセンベルグ(Hessenberg)行列にするのが普通です。
ヘッセンベルグ行列$B$は正方行列であり,
$$B=(b_{i,j})で,b_{i,j}=0(i \geqq j+2)$$
という性質を持ちます。
次に,反復計算の段階です。これにはQR法が用いられることが多いようです。
これは上で得られた上ヘッセンベルグ行列を$QR$法により上三角行列へと変換する方法です。
固有値は対角成分です。固有値が分かれば固有ベクトルは$(A-\lambda E)u=0$を解いて求めることができます。
中間形へ変換しない解法: ヤコビ法,べき乗法
対称行列専用の解法です。
ヤコビ(Jacobi)法
対称行列$A$を回転行列を用いた相似変換を繰り返すことで$A$を対角化する方法です。
固有値計算法の古典です。大規模行列は苦手ですが,行列の次数が小さいときは十分有用とのことです。
また,QR法よりも計算速度が劣るが固有値の精度は勝るという報告もあるそうです。
ヤコビ法のアルゴリズムはQR法と比べて柔軟で,同時対角化問題など固有値計算以外にも応用されるそうです。
#2017年9月28日: ヤコビ法についての記事を書きました。
[Pythonによる科学・技術計算] ヤコビ法による実対称行列の固有値・固有ベクトルの数値計算,数値線形代数
べき乗法
固有値の大小関係に着目します。基本的には絶対値最大の固有値を求める方法です。
#2017年9月12日: べき乗法についての記事を書きました。
[Pythonによる科学・技術計算]べき乗法による行列の固有値問題の数値解法,数値線形代数
QR法
対称・非対称行列の双方に適用可能で,すべての固有値を求めるアルゴリズムです。行列を直交行列と上三角行列に分けるQR分解とよばれる操作を行い,相似変換を繰り返します。
実用上は,
非対称行列の場合はヘッセンベルグ行列へ,対称行列の場合は3重対角行列に相似変換してからQR法を適用します。
手順は,固有値を求めたい行列を$A$として以下の通りです。
1. $A$を$QR$分解します。
2. 分解したものを逆順にかけあわせる
3. その結果をまたQR分解する
4. 2と3を繰り返す。
A_1 = Q_1 R_1
A_{k+1} = Q_k^{-1} A_k Q_k \, \, ( for \, k \geq 1)
A_{k+1} = Q_k^{-1} A_k Q_k = Q_k^{-1} ( Q_{k-1} A_{k-1} Q_{k-1}) Q_k = Q_k^{-1} ( Q_{k-1} (Q_{k-2} A_{k-2} Q_{k-2} )Q_{k-1}) Q_k =... \\
= Q_k^{-1} Q_{k-1}^{-1} Q_{k-2}^{-1} ... Q_{1}^{-1} A_1 Q_{1} ...Q_{k-2} Q_{k-1}
これにより,$k$が大きくなるにつれて$A_k$は$A$の固有値を対角成分にもつヘッセンベルグ行列に近づきます。**
固有ベクトルは,上で得られる固有ベクトル$(Q_k^{-1} Q_{k-1}^{-1} Q_{k-2}^{-1}... Q_{1}^{-1})x$に左から$ Q_{1}^{-1} A_1 Q_{1} ...Q_{k-2} Q_{k-1}$をかけることで求まります。
QR分解
$A=QR$
QはAの列ベクトルのグラム-シュミットの正規直交化,RはAの列ベクトルの正規直交基底に関する成分表示です。
QR分解にはハウスホルダー変換法などが用いられるようです。
QR分解は,以下のようにpythonのnp.linalg.qrメソッドで計算可能です。
例題
A =
\begin{pmatrix}
2 & 1 & 1 \\
1 & 2 & -2 \\
3 & 2 & 0 \\
\end{pmatrix}
として,
$A$をQR分解します。
import scipy.linalg as linalg
import numpy as np
A = np.array([[2, 1, 1],
[1, 2, -2],
[3, 2, 0]])
Q, R = np.linalg.qr(A)
print("Q=",Q)
print("R=",R)
==> 結果
Q= [[-0.53452248 0.31448545 -0.78446454]
[-0.26726124 -0.94345635 -0.19611614]
[-0.80178373 0.10482848 0.58834841]]
R= [[ -3.74165739e+00 -2.67261242e+00 2.22044605e-16]
[ 0.00000000e+00 -1.36277029e+00 2.20139816e+00]
[ 0.00000000e+00 0.00000000e+00 -3.92232270e-01]]
となり, 直交行列のQと上三角行列のRに分解されました。
求まったQとRの積がAになるのか確かめます。
QR=np.dot(Q, R)
print("QR=",QR)
==> 結果
QR= [[ 2.00000000e+00 1.00000000e+00 1.00000000e+00]
[ 1.00000000e+00 2.00000000e+00 -2.00000000e+00]
[ 3.00000000e+00 2.00000000e+00 -5.55111512e-17]]
QRは数値精度内でAと一致しており,Aは正しくQR分解されたことが確かめられました。
参考文献
[1] 森正武,杉原正顕,室田一雄『岩波講座 応用数学 線形計算 』,岩波書店,1993.
[2] 名取亮,線形計算, 朝倉書店,1993.
[3] ネットで閲覧可能[○×的数学のお部屋] (http://marupeke296.com/oxmath_no3_eigenvalues.html)
[4] Qiita記事, [Pythonによる科学・技術計算] 数値線形代数でヒンパンに出てくる行列の一覧
[5] Qiita記事, [Pythonによる科学・技術計算]べき乗法による行列の固有値問題の数値解法,数値線形代数
[6] Qiita記事, [Pythonによる科学・技術計算] ヤコビ法による実対称行列の固有値・固有ベクトルの数値計算,数値線形代数