はじめに
係数行列$A$を対称行列とした標準固有値問題
$$Ax = \lambda x \tag {1}$$
において,Aを対角行列にする直交行列$P$が存在することを利用して全ての固有値・固有ベクトルをヤコビ法と呼ばれる方法によって求めます。
内容
1. ヤコビ法の概略
2. テスト計算: 4x4行列の固有値・固有ベクトルの数値計算
3. numpyを利用して求まる結果との比較
どんな人向け?
1. 行列の固有値問題の初歩を学びたい方
2. 比較的小さなサイズの固有値問題を解きたい方
3. 小規模な固有値問題に対してnumpyを使いたくない方(いる?)
1. ヤコビ(Jacobi)法
直交行列$R$による相似変換により対角化された$A$の行列を$A'$とします。
$$A' = R^{-1} A R \tag {2}$$
行列$R$の各列ベクトルは固有ベクトルとなります。
ヤコビ法はこのような$R$と$A'$の両方を逐次的に求める手法です。
以下,逐次計算過程における変換行列を$R_j$,それによる相似変換を$B_j$と記します。
すると,
$$ B_1 = R_1^{-1} A R_1$$
$$ B_2 = R_2^{-1} B_1 R_2 = R_2^{-1} R_1^{-1} A R_1 P_2$$
$$ B_3 = R_3^{-1} B_2 R_3 = R_3^{-1} R_2^{-1} R_1^{-1} A R_1 R_2R_3$$
...
$$ B_j = R_j^{-1} B_{j-1} R_j = R_j^{-1}...R_3^{-1} R_2^{-1} R_1^{-1} A R_1 R_2R_3...R_j$$
となります。
$R$によるAの相似変換を繰り返すことで$B$が対角行列に近づいていきます。その対角成分が求める固有値です。
また,そうしてもとまった変換行列$R$
$$R = \lim_{n \to \infty} R_1 R_2R_3...R_n$$
の各々の列ベクトルが固有ベクトルです。
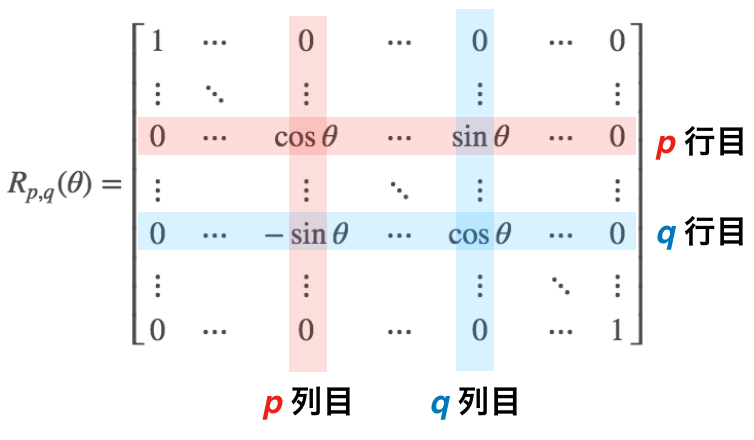
ここで,$R_j$は,行列$B_j$の非対角要素の中で絶対値が最大のものが$p$行$q$列目にある場合*に,以下の行列で与えられます。これはギブンス回転行列と呼ばれています。
$R_j$における$\theta$は,$B_j$の行列要素を$b_{pq}$などと書くと,
$$\theta = \frac{1}{2}Arctan(\frac{2 b_{pq}}{b_{pp}-b_{qq}}) \tag {5}$$
となります。
$b_{pp}-b_{qq} =0$となる場合は,
$$\theta = \frac{\pi}{4} \tag {6}$$
となります。
相似変換を行うたびに$\theta$を計算することで,$B$が次々に更新されていきます。
新しい$B$の行列要素を$b_{pq}'$, 古い$B$のそれを$b_{pq}$とかくと,$b_{pq}'$は以下のように表せます。
$ b_{pq}' = b_{qp}' = 0 $
$ b_{p,k}' = b_{bk} cos(\theta) - b_{qk}sin(\theta) \ (k \ne p, q)$
$ b_{q,k}' = b_{bk} sin(\theta) + b_{qk}cos(\theta)\ (k \ne p, q)$
$b_{pp}' = \frac{(b_{pp}+b_{pq})}{2}+ \frac{(b_{pp}-b_{pq})}{2} cos(2\theta)-b_{pq}sin(2\theta)$
$b_{qq}' = \frac{(b_{pp}+b_{pq})}{2}- \frac{(b_{pp}-b_{pq})}{2} cos(2\theta)+b_{pq}sin(2\theta)$ $\tag {7}$
以上,固有値・固有ベクトル計算に必要な計算をまとめると,
- $B_{j-1}$の絶対値最大の要素のインデックス(p,q)を調べる
- 式(5,6)から$\theta$を計算する
- $B_j$を式(7)により構築する
- ギブンス回転行列$R_{j,pq}(\theta)$を構築する
- 新しい$R$として$R=(R_1 R_2.... R_{j-1}) R_{j}$を構築する
- 1-5を望みの精度に到達するまで繰り返す。
収束条件は,非対角項の絶対値の最大値がある程度小さくなることとします。
2. 計算コード: ヤコビ法のテスト計算
"""
ヤコビ法による固有値問題
Sept. 2017
ok
"""
import numpy as np
A=np.array( [[1,2,3,4],[2,5,4,0],[3,4,1,1],[4,0,1,2]]) ## テスト計算用行列
B=np.array([len(A),len(A)])
C=np.array([len(A),len(A)])
R=np.identity(len(A))
qri =1e-8 # 収束条件: 非対角成分の最大値
def max_non_diag_abs_val(A): #非対角成分の絶対値をとり,対角項を0にする
C = np.abs(A)
for i in range(len(A)) :
C[i,i] = 0
return np.max(C)
def search_max_index(A): # 非対角成分の絶対値の最大値を求める。
C = np.abs(A)
for i in range(len(A)) :
C[i,i] = 0
index=np.argmax(C)
index_list=[]
p = index // len(C)
q = index % len(C)
index_list.append(p)
index_list.append(q)
return index_list
def elim_diag(AA,p,q): : # Bの相似変換: B_{j-1} -> B_jへ
D = np.zeros([len(AA),len(AA)])
D[:,:] = AA[:,:]
if AA[p,p]-AA[q,q] ==0 :
print("hit")
phi = np.pi/4
else:
phi = 0.5*np.arctan(-2*AA[p,q]/(AA[p,p]-AA[q,q]))
#
for k in range(len(AA)):
D[p,k] = AA[p,k]*np.cos(phi) - AA[q,k]*np.sin(phi)
D[k,p] = D[p,k]
D[q,k] = AA[p,k]*np.sin(phi) + AA[q,k]*np.cos(phi)
D[k,q] = D[q,k]
D[p,p] = (AA[p,p]+AA[q,q])/2+ ((AA[p,p]-AA[q,q])/2)*np.cos(2*phi)-AA[p,q]*np.sin(2*phi)
D[q,q] = (AA[p,p]+AA[q,q])/2- ((AA[p,p]-AA[q,q])/2)*np.cos(2*phi)+AA[p,q]*np.sin(2*phi)
D[p,q] = 0.0
D[q,p] = 0.0
return D, phi # 新しいBとギブンス回転角phiを返す
def make_ortho_mat(R,p,q,phi): ギブンス回転行列の構築
RR = np.identity(len(A))
RR[p,p] = np.cos(phi)
RR[p,q] = np.sin(phi)
RR[q,p] = -np.sin(phi)
RR[q,q] = np.cos(phi)
return np.dot(R,RR)
#
n_step = 0
B=A
non_diag_max= max_non_diag_abs_val(B)
print(A)
print ("n_step=",n_step,", non_diag_max=",non_diag_max )
# メインループ
while (non_diag_max) >= qri: 非対角成分がqri以下になるまで計算を繰り返す
n_step += 1
max_index=search_max_index(B)
p = max_index[0]
q = max_index[1]
B,phi = elim_diag(B,p,q)
R = make_ortho_mat(R,p,q,phi)
non_diag_max= max_non_diag_abs_val(B)
print ("n_step=",n_step,", non_diag_max=",non_diag_max )
# 結果の表示
print()
print("eigen_vectors",R.T)
print("eigen values = ", np.diag(B))
結果:
A=
[[1 2 3 4]
[2 5 4 0]
[3 4 1 1]
[4 0 1 2]]
繰り返し過程
n_step= 0 , non_diag_max= 4
n_step= 1 , non_diag_max= 4.0
n_step= 2 , non_diag_max= 2.56384550459
n_step= 3 , non_diag_max= 1.73602695462
n_step= 4 , non_diag_max= 1.34178492675
n_step= 5 , non_diag_max= 1.0541659557
n_step= 6 , non_diag_max= 1.00991605971
n_step= 7 , non_diag_max= 0.679264865395
n_step= 8 , non_diag_max= 0.0969781614884
n_step= 9 , non_diag_max= 0.0631869713238
n_step= 10 , non_diag_max= 0.0572533841424
n_step= 11 , non_diag_max= 0.047207989682
n_step= 12 , non_diag_max= 0.0319077318389
n_step= 13 , non_diag_max= 0.000638322066564
n_step= 14 , non_diag_max= 0.000507956168957
n_step= 15 , non_diag_max= 0.000338091900869
n_step= 16 , non_diag_max= 2.21020050554e-06
n_step= 17 , non_diag_max= 1.88809555444e-07
n_step= 18 , non_diag_max= 1.2549716462e-07
n_step= 19 , non_diag_max= 1.36872751979e-13
解
固有ベクトル
[[ 0.75143915 0.03374072 -0.44550604 -0.48551533]
[ 0.47493892 0.64751621 0.50463142 0.31702195]
[ 0.18749369 -0.50424687 0.73256339 -0.41705165]
[ 0.41787359 -0.57036779 -0.10110577 0.69988561]]
固有値
[-3.27326416 9.58429221 -1.55480701 4.24377896]
3. numpy を利用した結果との比較
[Pythonによる科学・技術計算] numpy・scipyを用いた(一般化)固有値問題の解法,ライブラリ利用(https://qiita.com/sci_Haru/items/034c6f74d415c1c10d0b)
を参考にする。
import numpy as np
"""
実行列の固有値・固有ベクトルの計算
# ライブラリ利用
"""
A=np.array( [[1,2,3,4],[2,5,4,0],[3,4,1,1],[4,0,1,2]])
eig_val, eig_vec =np.linalg.eig(A) # 固有値・固有ベクトルをそれぞれeig_val, eig_vecに格納する
for i in range(len(eig_vec)): #正規化
eig_vec [i] = eig_vec[i]/np.linalg.norm(eig_vec[i])
# 計算結果の出力
print(eig_vec.T)
print (eig_val)
固有ベクトル
[[ 0.47493892 0.64751621 0.50463142 0.31702195]
[ 0.41787359 -0.57036779 -0.10110577 0.69988561]
[ 0.75143915 0.03374072 -0.44550604 -0.48551533]
[-0.18749369 0.50424687 -0.73256339 0.41705165]]
固有値
[ 9.58429221 4.24377896 -3.27326416 -1.55480701]
ヤコビ法で求めた結果と良く一致しています。
これで,ヤコビ法で固有値・固有ベクトルを正しく計算できたことが示されました。
補遺
ヤコビ法による行列の固有値・固有ベクトルを求めるための演算回数は行列のサイズ$n$の2乗に比例します。
行列サイズが大きい固有値問題に対してヤコビ法は実用的ではなくなります。この場合はQR法などを用いるようです[1]。
ヤコビ法はある程度の大きさ($n$が数十程度)までの固有値計算では実用に耐えられそうです。
参考文献
[1] 戸川隼人,『マトリクスの数値計算』, オーム社, 1971.
[2] 非対角成分の絶対値の最大値を求める: [Pythonによる科学・技術計算] 正方行列の最大(最小)要素の行・列のインデックスの取得, numpy
[3] 絶対値最大の固有値を求めるべき乗法はこちら: [Pythonによる科学・技術計算]べき乗法による行列の固有値問題の数値解法,数値線形代数