はじめに
前回は、行列を使って3Dの透視変換を実現する方法を解説しました。
今回は、行列の値を変更して、画面のアスペクト比と画角を調整してみましょう。
1. アスペクト比を調整する
まずはアスペクト比を調整してみます。
現在は、ウィンドウ内部のビューの大きさを横640ピクセル×縦480ピクセルに設定していますので、横が縦よりも1.33...倍長い計算になります。この1.33という値が、4:3の画面におけるアスペクト比です。これまでは縦も横も-1.0〜1.0の範囲となるように頂点データを書いてきましたが、これでは同じ長さの線でも、縦よりも横の線の方が長く表示されてしまいます。
そこで、X座標を-1.33〜1.33の範囲にすることによって、同じ大きさの縦の線と横の線の長さが均等に表示できるようにします。もちろんX座標を-1.0〜1.0の範囲のままにして、Y座標の範囲を-0.75〜0.75にしても同じことなのですが、画面のサイズは縦を基準にするのが慣例ですので、X座標の範囲の方を調整します。
X座標の範囲を-1.33〜1.33とした後、これを描画する際にはシェーダ内の座標である-1.0〜1.0の座標に戻さねばなりません。それは、アスペクト比1.33(=4/3)の逆数である0.75(=3/4)をX座標に掛けることによって実現できます。
さて、前回作成した行列において、X座標に掛け合わせられる値は要素11ですから、ここを0.75にすることによって、アスペクト比を調整することができます。
program->Use();
GLKMatrix4 mat = GLKMatrix4Make(0.75f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, -0.01f, 0.0f);
program->SetUniform("mat", mat);
それでは、縦横の長さが同じ直角三角形の頂点データを用意して、この行列を使って描画してみましょう。
data.push_back({ { -0.6f, -0.5f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.4f, -0.5f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.4f, 0.5f, 1.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, -0.5f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.2f, -0.5f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.2f, 0.5f, 2.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
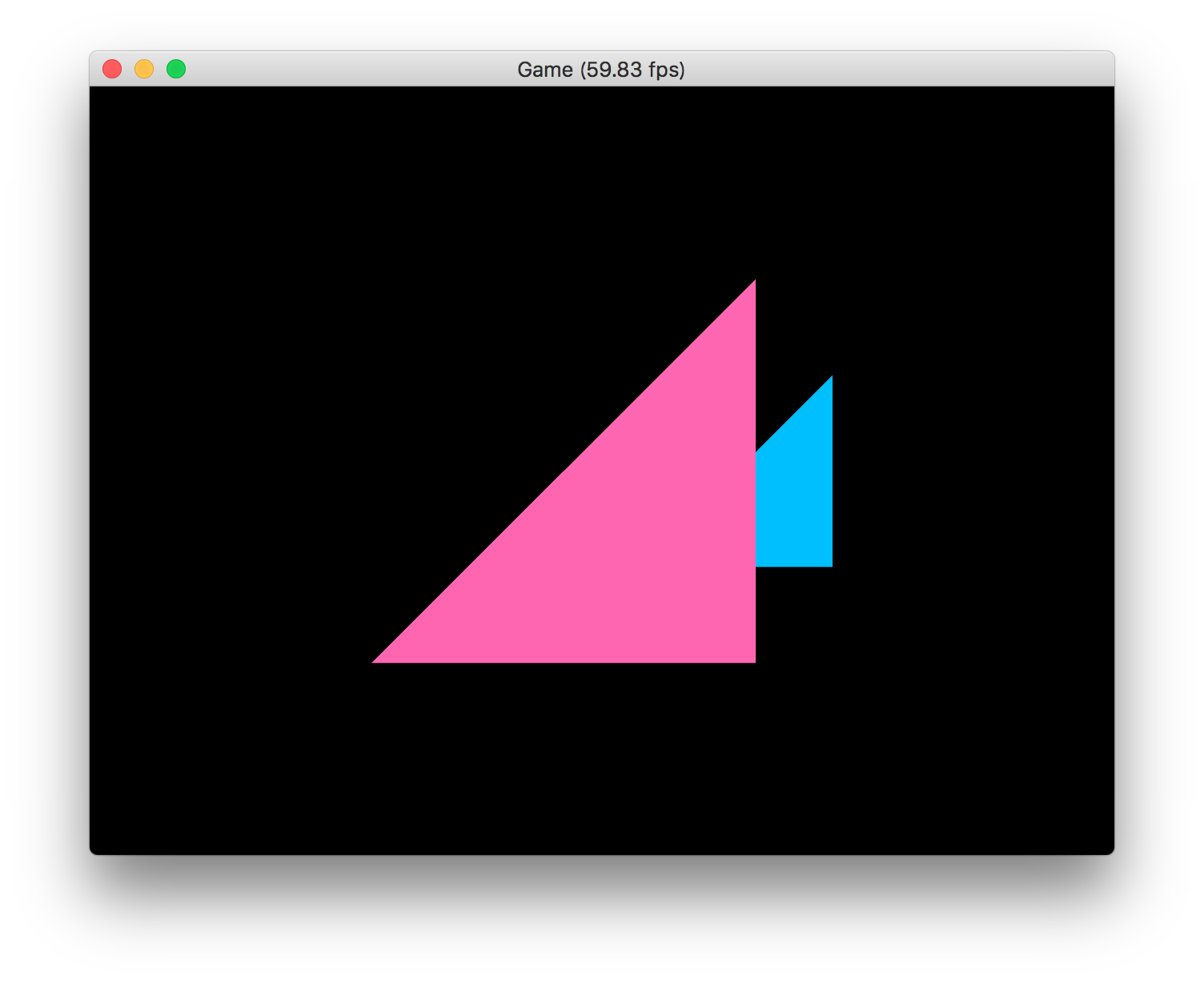
実行結果は次のようになります。
ここまでのプロジェクト:MyGLGame_step3-4a.zip
ピンク色の三角形も、水色の三角形も、縦横の高さが同じになって表示されるようになったことが分かります。
2. 画角を調整する(その1)
次に、画角を調整しましょう。
画角というのは、カメラに映る範囲を表す角度です。これまで見てきたように、透視変換はX座標とY座標をZ座標で割ることによって実現されていますので、z=1の平面上におけるy=1.0の点はy=1.0(すなわち画面上端)に表示されますし、y=-1.0の点はy=-1.0(すなわち画面下端)に表示されます。
これを図にすると、次のようになります。
この状態の画角を、90°の画角と言います。つまり、何もいじっていない状態では、90°の画角となるような変換行列になるのです。
それでは、もう少し広い範囲を見渡せる画角にしてみましょう。次の図のように、120°の画角を考えてみます。
角度が60°であるこのような直角三角形において、底辺の長さが1なら、高さは1.73 (=√3) になります。すなわち、画角が120°になると、Y座標の範囲は-1.73〜1.73の範囲に広がります。
画角が120°の世界を設定し、Y座標の範囲が-1.73〜1.73となるようにしたら、y=1.73のデータをレンダリングする際に、その値はy=1.0に変換されるようにする必要があります。つまり、1.73の逆数である0.58を掛ける操作が必要になります(正確には1/√3=0.5773...です)。
それでは、画角を120°にする調整を行列に組み込みましょう。X座標とY座標に掛けられる要素11と要素22のそれぞれに、0.58を掛けておきます。
GLKMatrix4 mat = GLKMatrix4Make(0.75f * 0.58f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f * 0.58f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, -0.01f, 0.0f);
なお、画角のことをfovy(field-of-view-y)とも呼ぶのですが、画角はY座標に対する画角を基準として考えます。そのため、同じ比率をアスペクト比を調整した後のX座標の成分にも掛け合わせています。
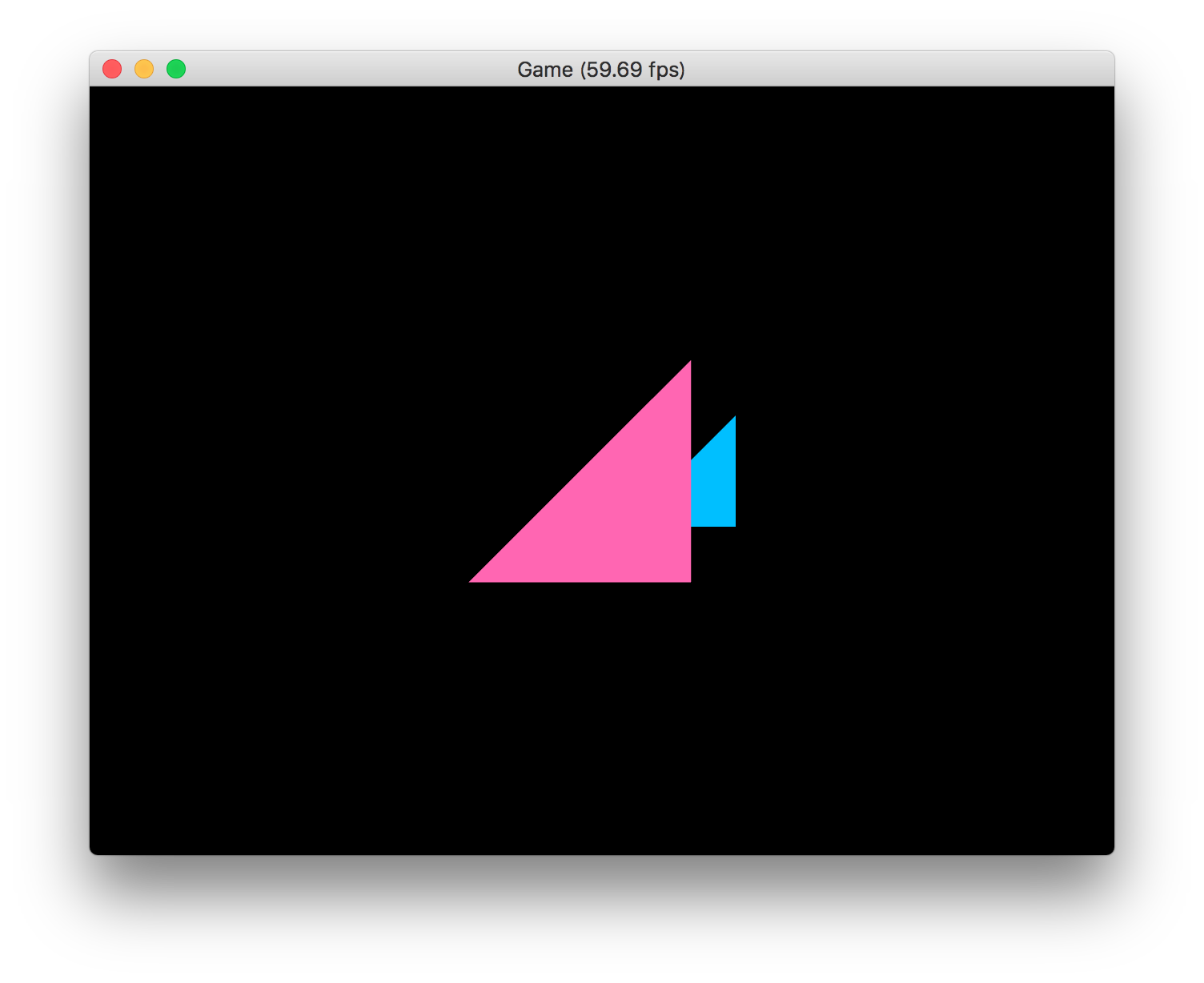
実行結果は次のようになります。先程までの表示がちょうど半分の大きさになったことから、画角が上下に(そして左右にも)広がったことが分かるでしょう。
ここまでのプロジェクト:MyGLGame_step3-4b.zip
3. 画角を調整する(その2)
それでは、どのような画角でも表せるように、手順2で行列の要素11と要素22に掛け合わせた0.58という値を、角度から算出できるようにしてみましょう。
掛け合わせる値は、高さに対する底辺の比率でした。先程は、120°の画角に対して、その半分の60°の角度を頂点にもつ直角三角形を考えたので、底辺1に対して高さ√3となり、高さに対する底辺の比が1/√3≒0.58となったのです。
さて、高校時代に習う三角比として、角度を元に「底辺に対する高さの比」を計算するタンジェント (Tangent) という計算があります。「高さに対する底辺の比」はその逆数ですから、画角の半分の角度に対するタンジェントを求めて、その逆数を計算すれば、掛け合わせる値が求まります。
これをコードにすると、次のようになります。
float fovy = GLKMathDegreesToRadians(120.0f);
float cot = 1.0f / tanf(fovy / 2);
GLKMatrix4 mat = GLKMatrix4Make(0.75f * cot, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f * cot, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, -0.01f, 0.0f);
タンジェントの逆数のことを、コタンジェント (Cotangent) と言いますので、ここではタンジェントの逆数を格納する変数にcotという名前を付けています。
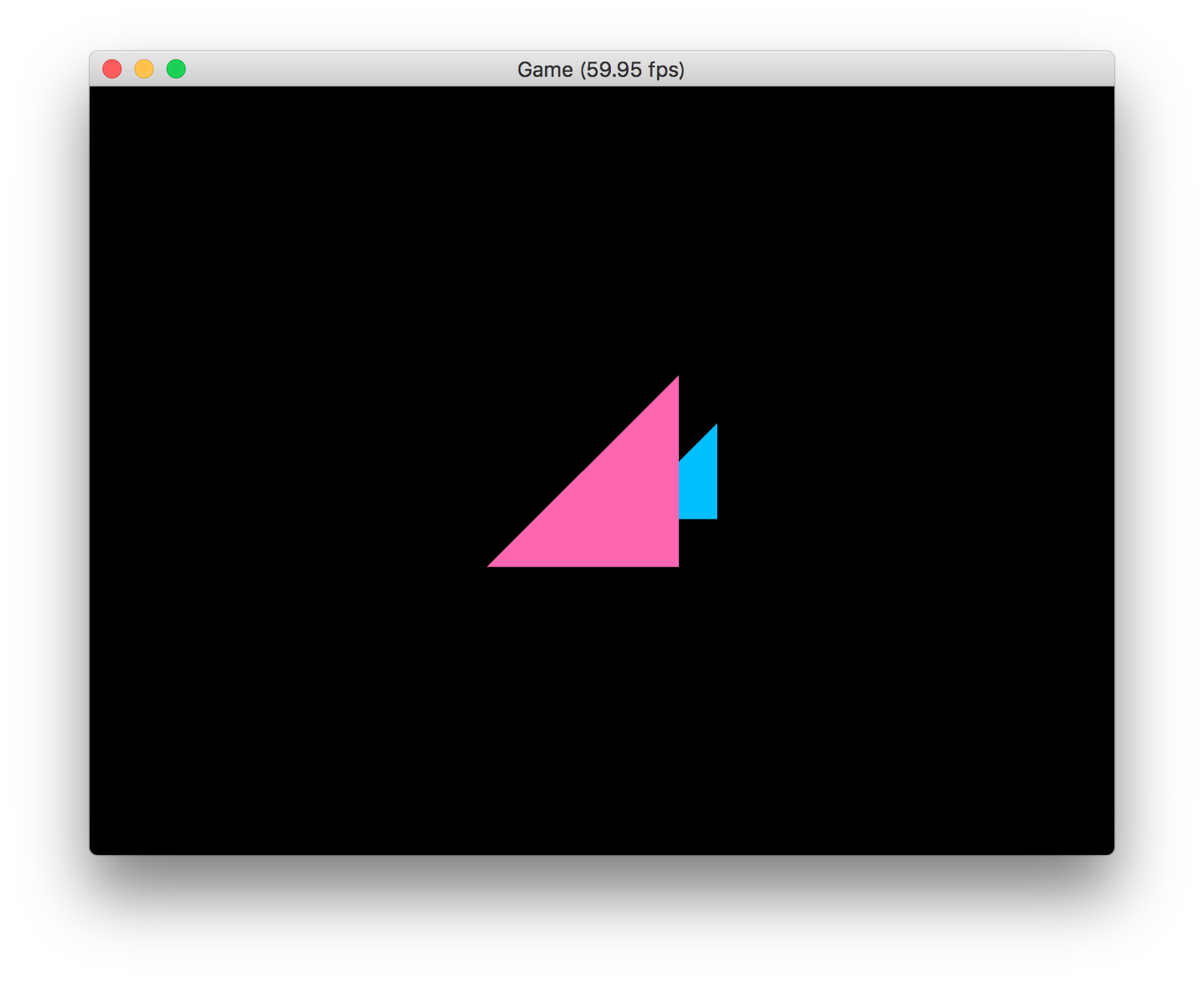
画角を120°から60°に変更してみましょう。
float fovy = GLKMathDegreesToRadians(60.0f);
次のような実行結果になって、今度は逆に視野が狭くなったことが確認できます。
ここまでのプロジェクト:MyGLGame_step3-4c.zip
4. まとめ
今回は、行列の値を書き換えることによって、アスペクト比の調整と、画角の調整ができることを解説しました。
- 行列の要素11にアスペクト比の逆数を掛けることで、アスペクト比が調整できます。
- 行列の要素11と要素22に画角の1/2の角度のコタンジェントを掛けることで、画角が調整できます。
実用的なOpenGLのプログラミングをする際には、さらに、カメラのレンズが奥行き方向のどの範囲を映すのかという、near-zとfar-zという値を指定しなければいけません。次回はその奥行き方向の範囲の調整について解説しましょう。