はじめに
前回は、同次座標を使って3Dの透視変換が行えることを説明しました。
今回は、行列を使って前回と同じ透視変換を実現してみましょう。
1. 頂点シェーダを書き換える
まずは頂点シェーダを、次のように書き換えます。
# version 410
layout (location=0) in vec3 vertex_pos;
layout (location=1) in vec4 vertex_color;
uniform mat4 mat;
out vec4 color;
void main()
{
gl_Position = vec4(vertex_pos, 1.0) * mat;
color = vertex_color;
}
uniform変数として4x4行列のmat変数を1つ用意し、3次元ベクトルであるvertex_pos変数に、第4の項目wを1.0で補った4次元ベクトルをその行列に掛け合わせて、算出される結果をgl_Position変数に格納します。
2. ShaderProgramクラスにメソッドを追加する
シェーダのuniform変数に行列の値を受け渡すために、ShaderProgramクラスにSetUniform()関数のオーバーロードを追加します。また同時に、2次元ベクトル, 3次元ベクトル, 4次元ベクトルも将来的に受け渡せるように、GLKVector2, GLKVector3, GLKVector4構造体のためのSetUniform()関数のオーバーロードも追加しましょう。
まずはShader.hppに、次のように関数の宣言を追加します。
...
# include <GLKit/GLKMath.h>
...
class ShaderProgram
{
...
void SetUniform(const std::string& name, const GLKVector2& vec);
void SetUniform(const std::string& name, const GLKVector3& vec);
void SetUniform(const std::string& name, const GLKVector4& vec);
void SetUniform(const std::string& name, const GLKMatrix4& mat);
...
};
次に、これらの関数の実装を、Shader.cppに次のように追加します。
void ShaderProgram::SetUniform(const std::string& name, const GLKVector2& vec)
{
GLint location = GetUniformLocation(name);
glUniform2fv(location, 1, vec.v);
}
void ShaderProgram::SetUniform(const std::string& name, const GLKVector3& vec)
{
GLint location = GetUniformLocation(name);
glUniform3fv(location, 1, vec.v);
}
void ShaderProgram::SetUniform(const std::string& name, const GLKVector4& vec)
{
GLint location = GetUniformLocation(name);
glUniform4fv(location, 1, vec.v);
}
void ShaderProgram::SetUniform(const std::string& name, const GLKMatrix4& mat)
{
GLint location = GetUniformLocation(name);
glUniformMatrix4fv(location, 1, GL_TRUE, mat.m);
}
GLKitのベクトルや行列を表す構造体には、x, y, zといったメンバ名に加えて、1次元配列として各要素にアクセスできるunion変数が、vやmといった名前で用意されています。これらの1次元配列の名前を書くことで、それをポインタとしてglUniform〜()系の関数にデータを渡すことができます。
3. Game::Game()を書き換える
Game::Game()に次のコードを追加して、行列を作成し、その行列をシェーダのuniform変数matに受け渡すようにしましょう。
Game::Game()
{
...
program->Use();
GLKMatrix4 mat = GLKMatrix4Make(1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, -0.01f, 0.0f);
program->SetUniform("mat", mat);
glClearColor(0.0f, 0.0f, 0.0f, 1.0f);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
}
ここまでできたら、ゲームを実行してみます。
ここまでのプロジェクト:MyGLGame_step3-3.zip
前回と同様の実行結果となり、3Dの透視変換が実現できていることが分かります。
4. 行列計算の解説
それでは、行列を使った計算で、値がどうなっているかを確認してみましょう。まず行列を作っている部分では、次のようにGLKMatrix4Make()関数を使って行列を作っています。
GLKMatrix4Make(1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 1.0f,
0.0f, 0.0f, -0.01f, 0.0f);
この行列がSetUniform()関数を通じてglUniformMatrix4fv()関数でシェーダ内のuniform変数matにセットされます。
そして頂点シェーダ内でgl_Position変数に代入される値は、頂点データにw=1.0の値を補った4次元ベクトルに、この行列を掛け合わせた結果となります。
gl_Position = vec4(vertex_pos, 1.0) * mat;
この計算を数式で表すと、次のようになります。
v =
\left(
\begin{matrix}
x & y & z & 1
\end{matrix}
\right)
\left(
\begin{matrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 1\\
0 & 0 & -0.01 & 0\\
\end{matrix}
\right)
これを計算すると、
v =
\left(
\begin{matrix}
x & y & z-0.01 & z
\end{matrix}
\right)
このような4次元ベクトルが算出されます(横ベクトルと行列の積については、このページの「横ベクトルと行列の積」などを参照してください)。
これを同次座標であるgl_Position変数に代入すると、4番目の項目の値でX座標, Y座標, Z座標が割られますので、最終的な値は、
v' =
\left(
\begin{matrix}
\frac{x}{z} & \frac{y}{z} & \frac{z-0.01}{z}
\end{matrix}
\right)
となります。前回と同じ計算結果になりますので、前回と同様の透視変換の計算が実現できているのが分かります。
5. まとめ
今回は、行列を使って3次元の頂点座標を変換し、同次座標の性質を活用した透視変換を実現する方法について解説しました。
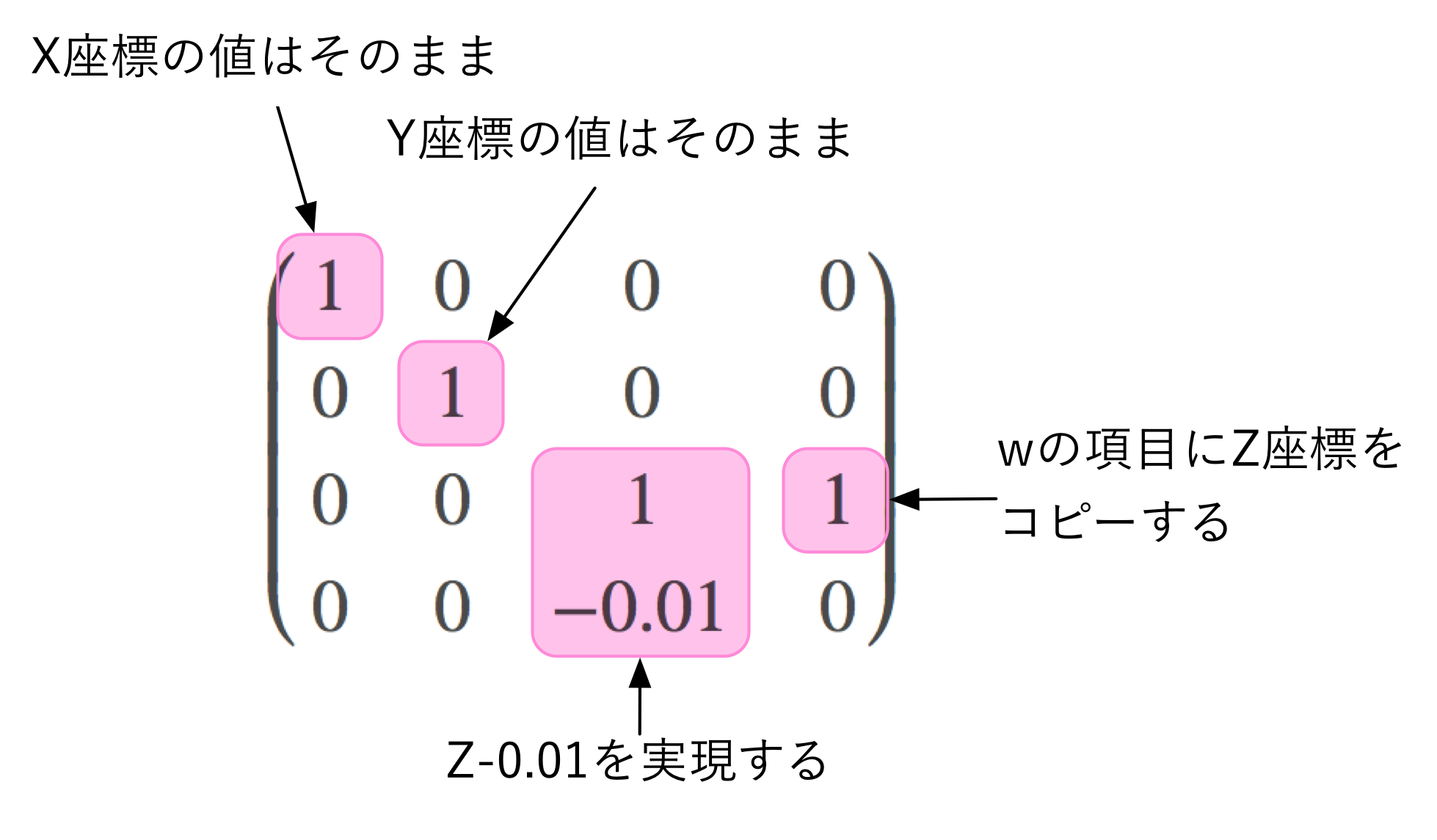
- 同次座標の
wの値にZ座標の値を入れる。 - Z座標の値から少し小さな値を引いておく。
という、透視変換に必要な操作が、行列によって実現できることが分かりました。
さて、同次座標だけで透視変換ができるのに、なぜ行列が必要なのでしょうか?
それは行列を使うことで、画角の調整、画面のアスペクト比の調整、カメラの移動や回転といった複数の操作が簡単に組み合わせられるようになるためです。次回は、画角と画面のアスペクト比を組み込む方法について解説しましょう。