はじめに
前回は、行列の要素11と要素22を修正することで、アスペクト比と画角の設定を行列に組み込めることを説明しました。
今回はさらに、行列の要素33と行列の要素34を修正することで、奥行方向の範囲調整が組み込めることを説明します。なお、これで透視変換を行う**「プロジェクション行列」と呼ばれる行列の作成はいったんの完成となりますが、ウェブ上で「透視変換行列」「プロジェクション行列」などのキーワードで検索できる行列には、大きく分けてOpenGL版とDirectX版の2種類**のものが出てきます。この記事では、両者の違いについても解説し、どちらを使うべきなのかについても見ていきましょう。
1. シェーダの座標系と奥行方向の調整
前回までは、最終的に計算されるZ座標の値がたまたま-1.0〜1.0の範囲に収まるようになっていましたが、実際にゲームを制作する場合には、様々な範囲のZ座標の頂点のデータを表示できるようにする必要があります。そのためには、表示したい範囲のZ座標の値を-1.0〜1.0の範囲に変換しなければいけません。
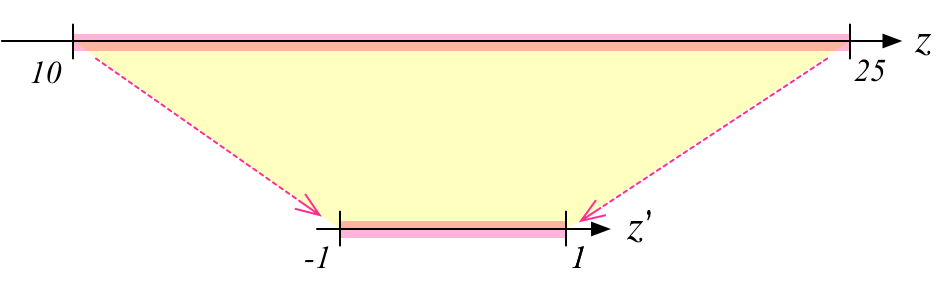
Z座標変換のイメージは次のような感じです。たとえばZ座標が10〜25の範囲にある頂点のデータを表示したければ、それを-1.0〜1.0の範囲に縮小します。
これを行列で計算するには、どうすれば良いでしょうか?
次のように、Z座標に関係する行列の要素33と要素34の値を、AとBと置いてみます(アスペクト比と画角の調整についてはとりあえず考えません)。なお、要素43の値を変えるとX座標とY座標の値にも影響が出ますので、要素43の値は1のままにしておきます。
\left(
\begin{matrix}
x' & y' & z' & w'
\end{matrix}
\right)
=
\left(
\begin{matrix}
x & y & z & 1
\end{matrix}
\right)
\left(
\begin{matrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & A & 1\\
0 & 0 & B & 0\\
\end{matrix}
\right)
これを計算すると、変換後の値は次のようになります。
\left(
\begin{matrix}
x' & y' & z' & w'
\end{matrix}
\right)
=
\left(
\begin{matrix}
x & y & Az+B & z
\end{matrix}
\right)
さらに同次座標の性質によって、最終的に使われるX座標、Y座標、Z座標の値は、次のようになります。
\left(
\begin{matrix}
x'' & y'' & z''
\end{matrix}
\right)
=
\left(
\begin{matrix}
\frac{x}{z} & \frac{y}{z} & \frac{Az+B}{z}
\end{matrix}
\right)
X座標とY座標に関してはこれまで通りですが、Z座標に関しては、AとBの値を求める必要があります。これは、中学校で習った連立1次方程式を使って解くことができます。
1-1. 奥行きを-1.0〜1.0の範囲に収める場合 (OpenGL)
何度も解説してきたように、GLSLのクリッピング領域は-1.0〜1.0です。もっとも手前のZ座標をn (near-z)、もっとも遠いZ座標をf(far-z)として、nが-1.0に、fが1.0に変換できるようなAとBの値を求めてみましょう。なお、0 < n < f となるような値だけを考えます(カメラ位置からゼロ距離にある物体は映すことができず、またカメラ位置よりも後ろにある物体も当然映らないため、Z座標はこの範囲で考えることになります)。
まず、元の頂点データのZ座標がnのとき、最終的なZ座標の値は、
\begin{align}
z''_n = \frac{An+B}{n} &= -1.0\\
\Leftrightarrow An+B &= -n&...(1)
\end{align}
となります(n > 0なので、両辺にnを掛けて整理しています)。
また、元の頂点データのZ座標がfのとき、最終的な値は、
\begin{align}
z''_f = \frac{Af+B}{f} &= 1.0\\
\Leftrightarrow Af+B &= f&...(2)
\end{align}
となります(f > 0なので、両辺にfを掛けて整理しています)。
(1)式を整理していくと、
\begin{align}
An+B &= -n\\
\Leftrightarrow B &= -An-n&...(3)
\end{align}
(2)式のBに(3)式のBを代入し、0 < n < f より f-n > 0 であることを利用すると、
\begin{align}
Af + (-An-n) &= f\\
\Leftrightarrow Af-An &= f+n\\
\Leftrightarrow A(f-n) &= f+n\\
\Leftrightarrow A &= \frac{f+n}{f-n} &...(4)
\end{align}
この(4)式を(3)式に代入します。事前にnを括り出しておいて、
\begin{align}
B &= -An-n\\
\Leftrightarrow B &= -n(A+1)\\
\Leftrightarrow B &= -n(\frac{f+n}{f-n}+1)\\
\end{align}
ここで、1を (f-n)/(f-n) に置き換えた上で、整理していきます。
\begin{align}
B &= -n(\frac{f+n}{f-n}+1)\\
\Leftrightarrow B &= -n(\frac{f+n}{f-n}+\frac{f-n}{f-n})\\
\Leftrightarrow B &= -n(\frac{f+n+f-n}{f-n})\\
\Leftrightarrow B &= -n(\frac{2f}{f-n})\\
\Leftrightarrow B &= \frac{-2fn}{f-n}\\
\end{align}
これにより、もっとも手前のZ座標をn (near-z)、もっとも遠いZ座標をf (far-z)と置いた時、その範囲のZ座標のデータを表示するための変換行列は、次のようになることが分かります。
\left(
\begin{matrix}
x' & y' & z' & w'
\end{matrix}
\right)
=
\left(
\begin{matrix}
x & y & z & 1
\end{matrix}
\right)
\left(
\begin{matrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & \frac{f+n}{f-n} & 1\\
0 & 0 & \frac{-2fn}{f-n} & 0\\
\end{matrix}
\right)
ここで、アスペクト比aspectと画角fovyから計算した調整のための値を要素11と要素22に掛けて、次のような透視変換のためのプロジェクション行列が求まります。
\left(
\begin{matrix}
\frac{1}{aspect}・\frac{1}{tan(fovy/2)} & 0 & 0 & 0\\
0 & \frac{1}{tan(fovy/2)} & 0 & 0\\
0 & 0 & \frac{f+n}{f-n} & 1\\
0 & 0 & \frac{-2fn}{f-n} & 0\\
\end{matrix}
\right)
OpenGLで昔から使われてきたプロジェクション行列を求める関数gluPerspective()のAPIリファレンスを見ると、掲載されている行列が転置されているため、要素34と要素43の位置が逆になり、またZ座標を前後反転させるために要素33と要素34に-1が掛けられてはいますが、上記と同じ計算が行われていることが確認できます。
1-2. 奥行きを0.0〜1.0の範囲に収める場合 (DirectX)
参考までに、DirectXが使用するHLSLについても見ておきましょう。
HLSLでは、GLSLと異なり、Z座標のクリッピング領域が0.0〜1.0となっています。そのため、プロジェクション行列として、near-zの値を0.0に、far-zの値を1.0に変換する行列を使用することになります。
1-1節の(1)式が、次のように少し変わります。
\begin{align}
z''_n = \frac{An+B}{n} &= 0.0\\
\Leftrightarrow An+B &= 0\\
\Leftrightarrow B &= -An&...(5)
\end{align}
1-1節の(2)式は変わりませんが、再掲すると次の通りです。
\begin{align}
z''_f = \frac{An}{f} &= 1.0\\
\Leftrightarrow Af+B &= f&...(2)
\end{align}
(2)式のBに(5)式のBを代入して、整理していきましょう。
\begin{align}
Af+B &= f\\
\Leftrightarrow Af+(-An) &= f\\
\Leftrightarrow Af-An &= f\\
\Leftrightarrow A(f-n) &= f\\
\Leftrightarrow A &= \frac{f}{f-n}&...(6)
\end{align}
(6)式を(5)式に代入して、Bを求めます。
\begin{align}
B &= -An\\
\Leftrightarrow B &= -\frac{f}{f-n}n\\
\Leftrightarrow B &= \frac{-fn}{f-n}
\end{align}
こうして求めたAとBを代入し、アスペクト比aspectと画角fovyの調整のための値を要素11と要素22に掛けて、次のような透視変換のためのプロジェクション行列が求まります。
\left(
\begin{matrix}
\frac{1}{aspect}・\frac{1}{tan(fovy/2)} & 0 & 0 & 0\\
0 & \frac{1}{tan(fovy/2)} & 0 & 0\\
0 & 0 & \frac{f}{f-n} & 1\\
0 & 0 & \frac{-fn}{f-n} & 0\\
\end{matrix}
\right)
DirectXに用意されている、プロジェクション行列を計算するための関数D3DXMatrixPerspectiveFovLH()のAPIリファレンスを見ると、これと同じ計算で行列が作られていることが確認できます。なお、この「macOSでOpenGLプログラミング」の記事とはまた違った透視変換の解説がDirect3Dの射影トランスフォームの解説記事に載っていますので、こちらも一度参考にすると良いでしょう。
1-3. どちらを使うべきなのか?
さて、1-1節と1-2節で、Z座標を-1.0〜1.0の範囲に変換する行列と、0.0〜1.0の範囲に変換する行列の、2種類の行列を求めました。私たちが使っているGLSLではどちらの行列を採用するべきなのでしょうか? HLSLでは元々Z座標を0.0〜1.0の範囲に収めなければいけませんから、DirectX用のバージョンしか使えないのですが、GLSLだとどちらでも使えそうに思えます。
計算式を見ると分かりますが、X座標とY座標はどちらを使っても値は変わりません。またZ座標はデプステストの際に使われる大小比較のための値ですので、どちらの行列を使っても大小関係が変わらない以上、どちらを使ってもほとんどの場合に問題は出ないと言えます。
ただし、例えば near-z=10, far-z=100という90もの範囲のデータが、-1.0〜1.0または0.0〜1.0という小さな範囲のデータに変換されるということを考えてください。カメラに近づくにつれて値が細かくなり、精度はどんどん落ちて大小関係が保たれるかどうかが怪しくなってしまいます。そう考えると、-1.0〜1.0の2.0の範囲に値を変換しておく方が、0.0〜1.0の1.0の範囲に抑えるよりも大小関係が保たれやすいと言えるでしょう。
そのためGLSLでは、1-1節で解説した、Z座標を-1.0〜1.0の範囲に変換する行列を採用していきましょう。
2. 頂点データを変更する
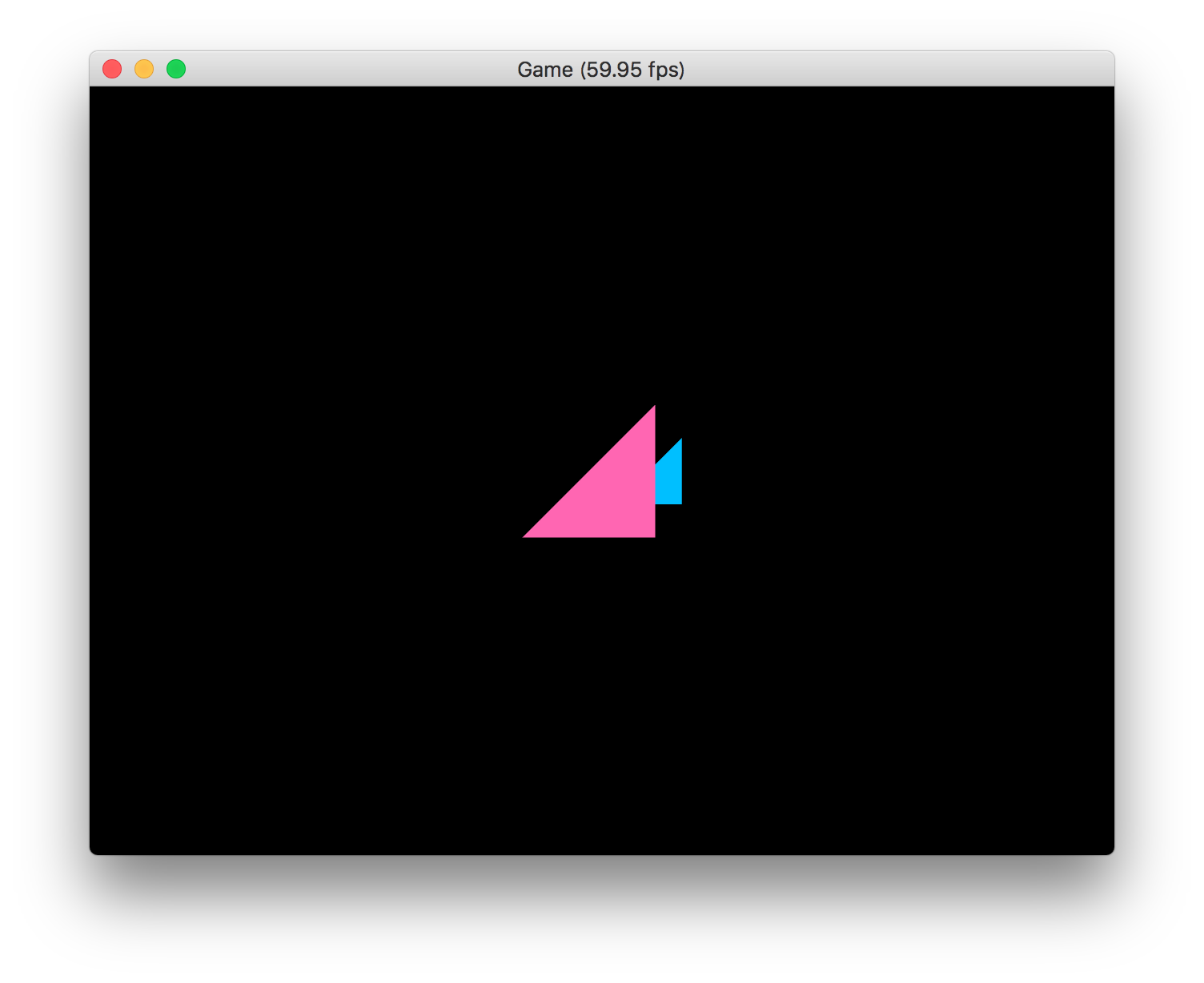
それでは大きなZ座標の頂点データでも、問題なく変換できるようになりましたので、頂点データに少し大きめのZ座標の値を指定してみましょう。手前のピンクの三角形のZ座標を5.0、奥側の水色の三角形のZ座標を10.0にします。
std::vector<VertexData> data;
data.push_back({ { -0.6f, -0.5f, 5.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.4f, -0.5f, 5.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.4f, 0.5f, 5.0f }, { 1.0f, 0.4f, 0.7f, 1.0f } });
data.push_back({ { 0.2f, -0.5f, 10.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.2f, -0.5f, 10.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
data.push_back({ { 1.2f, 0.5f, 10.0f }, { 0.0f, 0.75f, 1.0f, 1.0f } });
3. 行列を作るコードを修正する
行列を作ってuniform変数にセットするコードを、次のように変更します。行列の要素33と要素34に、1-1節で連立方程式を解いて算出した通りの計算式を使っています。
program->Use();
float aspect = 640.0f / 480.0f;
float fovy = GLKMathDegreesToRadians(60.0f);
float cot = 1.0f / tanf(fovy / 2);
float nearZ = 1.0f;
float farZ = 50.0f;
GLKMatrix4 mat = GLKMatrix4Make((1.0f / aspect) * cot, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f * cot, 0.0f, 0.0f,
0.0f, 0.0f, (farZ + nearZ) / (farZ - nearZ), 1.0f,
0.0f, 0.0f, -2 * farZ * nearZ / (farZ - nearZ), 0.0f);
program->SetUniform("mat", mat);
それでは実行してみましょう。次のように、手前から5m(1単位を1mとした場合)離れた位置に少し小さくピンク色の三角形が描画され、さらに5m離れた位置に、もっと小さく水色の三角形が描画されるようになったことが分かります。
ここまでのプロジェクト:MyGLGame_step3-5.zip
4. まとめ
今回は連立方程式を解いて、プロジェクション行列、すなわち、アスペクト比・画角・Z座標の描画範囲の調整をすべて盛り込んだ行列を作成しました。計算自体はとても簡単だったと思いますが、これが全世界で3Dの描画に使われているのと寸分違わぬ立派なプロジェクション行列です。
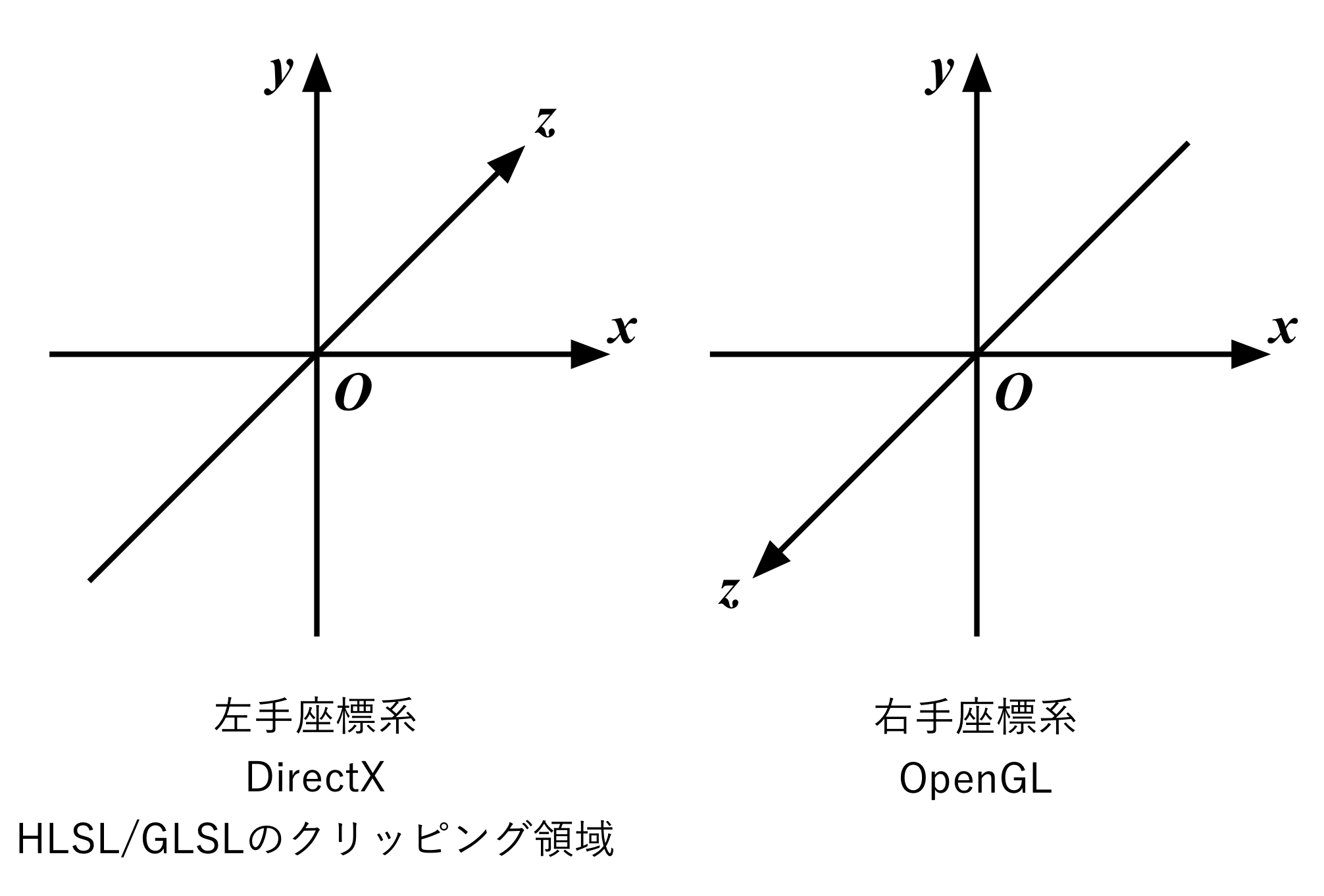
ただし、現在はGLSLの座標系に合わせてZ座標が0からプラスの方向に伸びると頂点データが奥に行くことにしていますが(これを左手系の座標系と言います)、OpenGLでは慣例として、Z座標が大きくなるほど頂点データが手前の方に来る、右手系と呼ばれる座標系が採用されることになっています。
ややこしいことに、GLSLのクリッピング領域は左手系ですが、OpenGL全体のAPIでは右手系でZ座標が処理されることに注意が必要です。
次回はGLKitに用意されたプロジェクション行列を使い、最初から右手系の座標系に合わせた行列を計算してくれる場合に、頂点データをどう扱うべきなのかを確認します。
次の記事:macOSでOpenGLプログラミング(3-6. GLKitのプロジェクション行列を使う(左手座標系→右手座標系))